Calculate the Distance Between Two Points in Java

1. Overview

In this quick tutorial, we'll show how to calculate the distance between two points in Java.

2. The Math Formula of the Distance

Let's say we have two points on a plane: the first point A has the coordinates (x1, y1), and the second point B has the coordinates (x2, y2). We want to calculate AB, the distance between the points.

Firstly, let's build a right triangle with the hypotenuse AB:

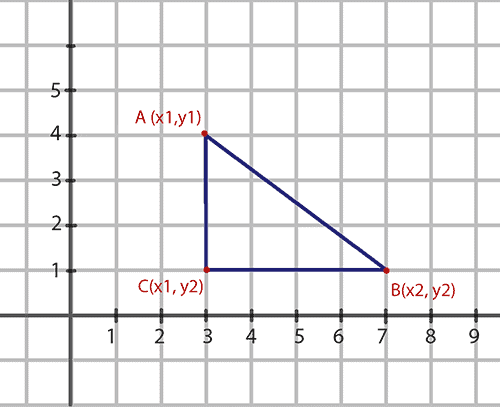
According to the Pythagorean theorem, the sum of the squares of the lengths of the triangle's legs is the same as the square of the length of the triangle's hypotenuse: AB² = AC² + CB².

Secondly, let's calculate AC and CB.

Obviously:

AC = y2 - y1

Similarly:

BC = x2 - x1

Let's substitute the parts of the equation:

distance * distance = (y2 - y1) * (y2 - y1) + (x2 - x1) * (x2 - x1)

Finally, from the above equation we can calculate the distance between the points:

distance = sqrt((y2 - y1) * (y2 - y1) + (x2 - x1) * (x2 - x1))

Now let's move on to the implementation part.

3. Java Implementation

3.1. Using Plain Formula

Although java.lang.Math and java.awt.geom.Point2D packages provide ready solutions, let's firstly implement the above formula as is:

public double calculateDistanceBetweenPoints(
  double x1, 
  double y1, 
  double x2, 
  double y2) {       
    return Math.sqrt((y2 - y1) * (y2 - y1) + (x2 - x1) * (x2 - x1));
}

To test the solution, let's take the triangle with legs 3 and 4 (as shown in the picture above).  It's clear that the number 5 is suitable as the value of the hypotenuse:

3 * 3 + 4 * 4 = 5 * 5

Let's check the solution:

@Test
public void givenTwoPoints_whenCalculateDistanceByFormula_thenCorrect() {
    double x1 = 3;
    double y1 = 4;
    double x2 = 7;
    double y2 = 1;

    double distance = service.calculateDistanceBetweenPoints(x1, y1, x2, y2);

    assertEquals(distance, 5, 0.001);
}

3.2. Using java.lang.Math Package

If the result of multiplication in the calculateDistanceBetweenPoints() method is too big, overflow can occur. Unlike that, Math.hypot() method prevents intermediate overflow or underflow:

public double calculateDistanceBetweenPointsWithHypot(
    double x1, 
    double y1, 
    double x2, 
    double y2) {
        
    double ac = Math.abs(y2 - y1);
    double cb = Math.abs(x2 - x1);
        
    return Math.hypot(ac, cb);
}

Let's take the same points as before and check that the distance is the same:

@Test
public void givenTwoPoints_whenCalculateDistanceWithHypot_thenCorrect() {
    double x1 = 3;
    double y1 = 4;
    double x2 = 7;
    double y2 = 1;

    double distance = service.calculateDistanceBetweenPointsWithHypot(x1, y1, x2, y2);

    assertEquals(distance, 5, 0.001);
}

3.3. Using java.awt.geom.Point2D Package

Finally, let's calculate the distance with the Point2D.distance() method:

public double calculateDistanceBetweenPointsWithPoint2D( 
    double x1, 
    double y1, 
    double x2, 
    double y2) {
        
    return Point2D.distance(x1, y1, x2, y2);
}

Now let's test the method in the same way:

@Test
public void givenTwoPoints_whenCalculateDistanceWithPoint2D_thenCorrect() {

    double x1 = 3;
    double y1 = 4;
    double x2 = 7;
    double y2 = 1;

    double distance = service.calculateDistanceBetweenPointsWithPoint2D(x1, y1, x2, y2);

    assertEquals(distance, 5, 0.001);
}

4. Conclusion

In this tutorial, we've shown a few ways to calculate the distance between two points in Java.

As always, the code used in the examples is available over on GitHub.

res – REST with Spring (eBook) (everywhere)

Learning to build your API
with Spring?

Download the E-book