From Lists to Forests | Baeldung on Computer Science

1. Introduction

In this tutorial, we’ll show how to turn a flat list into a tree or a forest.

2. Problem Statement

At input, we have a list of pairs representing a parent-child hierarchy. Each is a structure $(x, y)$ where $x$ is the ID of a node, and $y$ is the ID of its parent. Essentially, the pairs denote directed edges between the nodes in a hierarchy.

Further, the pairs may appear in any order. For example, node 2 is the parent of node 4 in this tree:

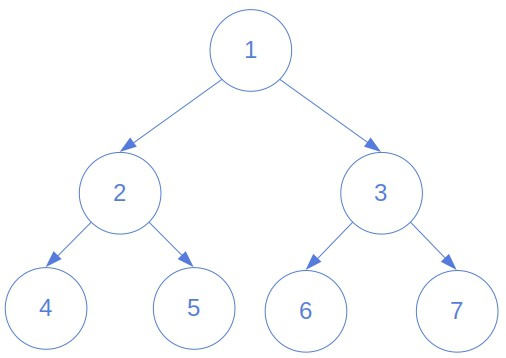
In any case, the pair $(2, 4)$ may come before $(1, 2)$ in the list.

What’s more, there may be several trees in the hierarchy. A node whose parent doesn’t appear as a child in the input list represents the root of an independent tree. Our goal is to turn the list into a set of trees, i.e., a forest if there’s more than one, and identify their roots.

The IDs may be of any type: integer numbers, string data, tuples, and so on. Finally, we’ll consider the general case and present solutions that work with all data types.

3. Solution

A straightforward way is to process the pairs one by one, find the parent’s node in the forest constructed so far, and attach the child to it. Then, if the parent isn’t already there, we create the corresponding node. But, that’s only a partial solution. Organizing the nodes into proper trees doesn’t mean much if we don’t identify their roots.

To find the roots, we use the following observation. If an ID appears as a child, we can rule it out as a potential root. So, if we start by considering all the nodes as candidate roots by default and rule out a candidate if we find its parent in the input list, only the actual roots will remain upon processing the whole list.

3.1. Proof of Correctness

Let’s prove the algorithm’s correctness. Our loop invariant is that $\boldsymbol{roots}$ contains all the nodes without known parents. We call such nodes candidate roots.

The invariant is trivially true before the loop since we initialize $roots$ to be an empty set.

Now, let’ suppose that the invariant holds before $i$ -th iteration. Is it so at the beginning of the next one as well? We analyze several cases:

If $child\_node$ is a candidate root, we rule it out and remove it from $roots$ .
If $child\_node$ isn’t a candidate root, it isn’t added to $roots$ .
If $parent\_node$ is a newly created node, it has no known parent, so we add it to $roots$ .
If $parent\_node$ isn’t a newly created node, we know it was added as another node’s child before, so we don’t include it into $roots$ .

So, we add to $roots$ a new node only if it’s a candidate root and remove a node that turns out to have a parent. Therefore, the invariant holds before the next loop. At the end of the algorithm, $\boldsymbol{roots}$ will contain only the actual roots and no other nodes.

3.2. Complexity

The lower bound of time complexity is $\Omega(n)$ since we have to process $n$ pairs, where $n$ is the input list’s length, i.e., the number of edges in the forest. Since each node has exactly one parent, $n$ also approximates the number of nodes. More precisely, $n$ is the difference between the number of nodes and the number of trees because the roots have no in-looking edges and won’t appear in the list.

The upper bounds depend on how we implement $FIND{-}OR-{CREATE}$ . If we don’t use an auxiliary data structure to memorize pairs for quick access, the memory complexity will be $\Theta(n)$ , but time complexity will become quadratic. That’s because in the worst case, we’ll traverse the whole forest to find the node with the given ID. So, we’ll do $\boldsymbol{i}$ lookups upon reading the $\boldsymbol{i}$ -th pair from the list, and the worst-case time complexity will be $\boldsymbol{O(n^2)}$ :

$\sum_{i=1}^{n}O(i)=O\left(\frac{n(n-1)}{2}\right) \in O(n^2)$

3.3. Variation with a Hash Table

If we use a hash table with node IDs as keys and pointers to the nodes as values, the average-case time complexity of $FIND{-}OR{-}CREATE$ will be $O(1)$ . So, the whole algorithm will be linear in the average case:

$\sum_{i=1}^{n}O(1) \in O(n)$

Everything in the pseudocode remains the same, except that we now maintain a hash table and use it in $FIND{-}OR{-}CREATE$ :

Moreover, since the set of keys won’t change upon creating the hash table, we can achieve perfect hashing. That means that the search will be $\boldsymbol{O(1)}$ even in the worst case. Consequently, our algorithm for building trees will become linear.

4. Trees as Connected Components

There’s another way to approach this problem. We can regard the input array as a list of edges in a (probably disconnected) graph. Upon reading all the edges, we start depth-first traversal from an arbitrary node and visit all the other nodes that belong to the same tree. The one with no parent represents the tree’s root. Repeating the process until we reach all the nodes, we identify the trees as connected components and collect their roots. The catch is that we have to maintain edges in both directions to visit the ancestors of the start node if we start the traversal from a non-root vertex.

4.1. Pseudocode

Here’s the pseudocode:

$DEPTH{-}FIRST$ is based on Depth-First Search (DFS):

4.2. Complexity

Reading the list and storing the nodes is $O(n)$ . Depth-First traversal doesn’t visit any node twice. So, the whole algorithm’s complexity may be linear. But, it depends on the way we implement $\boldsymbol{graph}$ . In particular, on whether or not we represent the edges with an adjacency matrix or adjacency lists.

In the former case, the $children$ attribute is a boolean row (we’ll have to map the IDs to natural numbers). For each node, we’ll need to pass through its whole row to find its children nodes. The algorithm would be of quadratic complexity. On the other hand, if we use adjacency lists, we’ll visit each node and cross each edge once. Since a tree with $m$ nodes contains $m-1$ edges, the $j$ -th call to $DEPTH{-}FIRST$ will take $O(m_j + m_j - 1) = O(m_j)$ time, where $m_j$ is the number of nodes in the $j$ -th tree. Summing over the trees, we get $O(n)$ .

4.3. Degenerate Input

The Depth-First approach can handle even the degenerate case where there are no edges. However, from the way the problem is defined, we see that such input is impossible. The reason is that it would correspond to an empty list, in which case no data would be available for processing, and no algorithm would be able to run.

5. Conclusion

In this article, we presented two algorithms for building a forest of trees from a flat list that contains the pairs of the form (child id, parent id). One algorithm is an ad-hoc solution we devised specifically for this problem. The other is an adaptation of the method for identifying connected components via Depth-First Search. Both can run in linear time, provided we use appropriate data structures.

Full Archive

About Baeldung

Core Concepts

Operating Systems

Artificial Intelligence

Graph Theory

Latex