Yes, we're now running our Black Friday Sale. All Access and Pro are 33% off until 2nd December, 2025:
Eigenvectors and Eigenvalues
Last updated: June 6, 2024
1. Introduction
In this tutorial, we’ll study eigenvectors and eigenvalues.
2. Eigenvectors and Eigenvalues
We can define a vector as a geometric object with two properties: magnitude and direction. Generally speaking, most vectors change magnitude and direction when undergoing some linear transformation (described by a square matrix), such as rotation, stretch, or shear.
Eigenvectors are nonzero vectors that don’t change direction when a specific linear transformation occurs. Hence, an eigenvector of a transformation is only stretched when we apply that transformation. The corresponding eigenvalue is the scalar by which an eigenvector gets stretched or compressed. If it’s negative, the transformation reverses the direction of the eigenvector.
2.1. Intuition
An eigenvector is like a pivot on which the transformation matrix hinges within the scope of a specific operation. The eigenvalue tells us how vital this pivot is within the operation’s scope and relative to the eigenvalues of other eigenvectors.
An eigenvector is a skewer that helps us keep a set of linear transformations in place. The corresponding eigenvalue is the power of this skewer. The eigenvalue measures the distortion of the transformation, and the eigenvector signifies the orientation of the distortion.
3. Mathematical Analysis
3.1. Definition
Let be an
square matrix and
be a nonzero column vector. Further on, we have a scalar
such that the following equation holds:
Then, is an eigenvalue of
, and
is an eigenvector of
corresponding to
. We call the set of all eigenvalues of a
the spectrum of
and denote it with
.
3.2. Eigenvector Equation
Let’s delve deep into the above equation.
We can write this equation as , where
is the identity matrix of the same order
. Next, we rearrange all terms on the left :
Here, we use to denote the zero matrix. This homogenous equation system has
variables and
values. So, it will have a unique solution if and only if the determinants of both matrices are equal:
To find the eigenvalues of any square matrix with dimensions
, we solve the characteristic equation
. That way, we get
eigenvalues. Next, for each
, we find its corresponding eigenvector by substituting
in
and solving for
using the elementary row transformations.
4. Example
We usually describe linear transformations in terms of matrices.
Let’s consider the following linear transformation matrix :
To find its eigenvalues, we need :
Now, we take the determinant:
Finally, we solve for
:
Thus, we get our two eigenvalues, , and
.
4.1. Eigenvectors
Next, we use these eigenvalues to get our two eigenvectors and
. First, we find
for
:
Then, we use elementary row transformation to reduce the bottom row to o (subtract row 2 from row 1) and equate the result to the zero vector:
Since and
can’t be zero, we get
. This gives us our
:
Similarly, we obtain our :
Also, any multiple of is the eigenvector of
corresponding to the eigenvalue
, and the same holds for eigenvector
.
4.2. Visualization
Let’s visualize what happens:
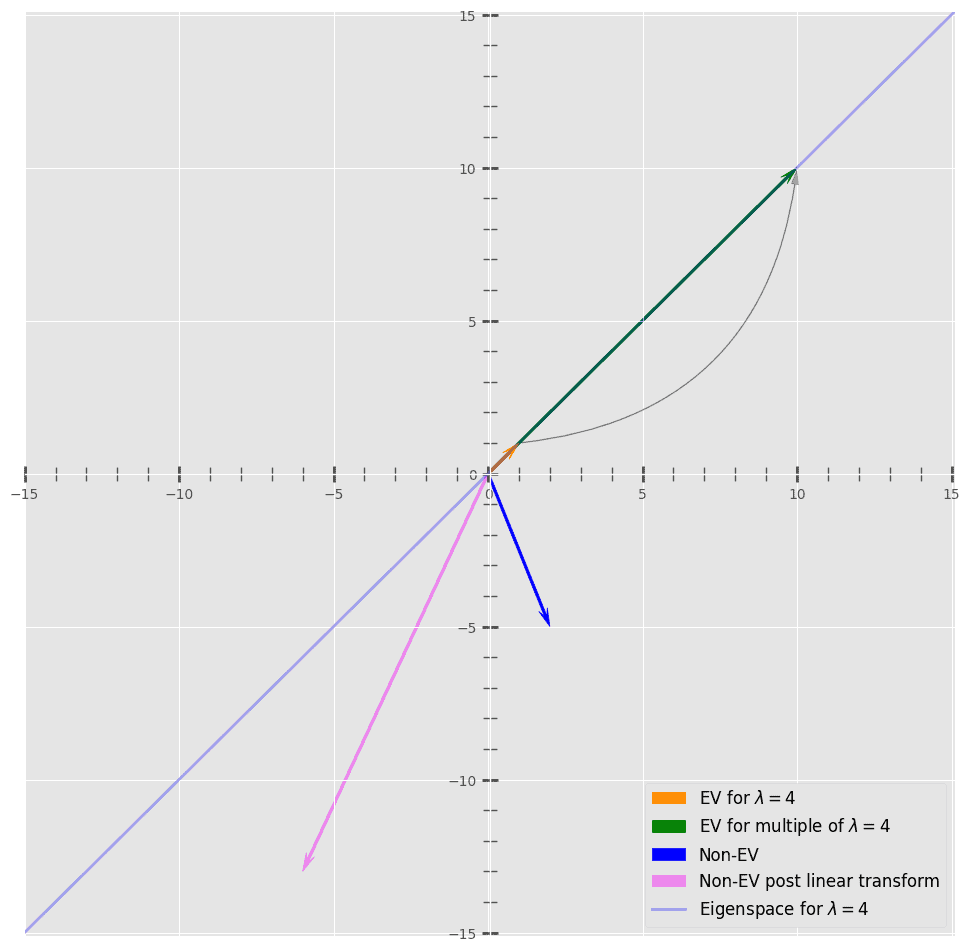
Here, we plotted and a non-eigenvector
along with their transformations
and
. Here, we can see that
doesn’t change direction after applying
, but
does.
5. Applications
5.1. Dimensionality Reduction and Eigenvectors
We use eigenvectors and eigenvalues to reduce noise in our data (e.g., using principal component analysis (PCA)). This helps us improve the efficiency of our computationally intensive tasks.
Let’s say we are to open a wine shop. We have 100 different types of wine and only ten shelves to fit them all. We devise an allocation strategy to put similar wines on the same shelf. Each wine differs in taste, color, price, texture, origin, fizz, etc.
First, we must know which qualities are most important for grouping similar wines. We can solve this problem with principal component analysis (PCA). PCA gives us the principal component variables that explain the variation between different wine groups. Each principal component can be a single original feature or a combination of features.
To determine the principal components of the data, we calculate eigenvectors and eigenvalues from the covariance matrix (a matrix capturing correlation between data). Let’s say that 95% of the variability between wine sorts is explained by the first principal component (eigenvector with the most considerable absolute value of the corresponding eigenvalue).
In that case, we can organize wine bottles on our shelves. Each shelf will contain bottles of wines similar in value along his eigenvector’s axis.
5.2. Eigenvector and Face Recognition
Eigenvectors are used in computer vision for face recognition tasks. Let’s say we have 1000 face images of a set of people and want to group photos according to their users. Further, we want to associate a new image with the person in it.
We can use eigenvectors for this. First, we use dimensionality reduction to derive a low-dimensional representation of face images. As a result, we get a collection of eigenfaces. Each eigenface is a face’s most crucial eigenvector (principal component).
We project the new image onto eigenfaces to get its representation and then find the closest representation of the existing faces in our face base.
Not only can we recognize faces but also reconstruct them using eigenfaces so that the visual difference is negligible while less memory is used:

In addition to this use case, we use this technique in handwriting, lip sync, voice, and gesture recognition.
6. Conclusion
In this article, we explained eigenvectors and eigenvalues. Eigenvalues and eigenvectors are associated with a square linear transformation matrix. An eigenvector is a nonzero vector that doesn’t change direction after applying a linear transformation. The corresponding eigenvalue is a scalar quantity that shows how much its magnitude changes.
Eigenvectors and eigenvalues are used in electrical circuits, mechanical systems, VLSI, deep learning, and graph algorithms (PageRank from Google). Moreover, all major computer vision tasks, such as face grouping, clustering, similarity search, dimensionality reductions, etc., use them in some form.