Learn through the super-clean Baeldung Pro experience:
>> Membership and Baeldung Pro.
No ads, dark-mode and 6 months free of IntelliJ Idea Ultimate to start with.
Last updated: March 18, 2024
In this tutorial, we’ll review the Principal Component Analysis (PCA), and we’ll describe how to use it by choosing the optimal number of principal components.
Finally, we illustrate the application of such a technique to a popular machine learning dataset.
Dimensionality reduction is the task of transforming data from a high dimensional space into a new space whose dimensionality is much smaller. Dimensionality reduction is closely related to the process of data compression in the signal processing field.
In machine learning, dimensionality reduction is generally used to speed up the training of a model. Moreover, in some cases reducing the dimensionality of data may filter out noisy features, and models with higher accuracy are obtained. Dimensionality reduction is also useful for data visualization and for finding a meaningful interpretation of the data. In fact, reducing the dimensions down to two or three allows to represent high dimensional data on a plot and obtain relevant information.
PCA is the most popular dimensionality reduction technique. In PCA, the compression and the recovery are performed by means of linear transformations; the algorithm finds the linear transformations for which the mean squared error computed over a set of instances is minimal.
Given a set of feature vectors
in
, a real matrix
of size
, where
, is used to reduce the dimensionality of
by performing the linear transformation
. A real matrix
of size
is used to approximately reconstruct each original vector
from the compressed version
by performing the transformation
; hence,
is the recovered version of the original feature vector
and it has the same dimensionality
. The PCA consists in finding the compression matrix
and the recover matrix
such that the mean squared error computed over the set of instances is minimal, i.e., the following problem is solved:
(1)
It can be demonstrated that if and
are solutions of Eq.
, then it must be
. Hence, the recover matrix
is obtained by transposing the compression matrix
. Moreover it can be demonstrated that the columns of the matrix
, solution of Eq.
, correspond to the eigenvectors of the sample covariance matrix of the data
.
We remind that the covariance matrix is defined as:
(2)
where is a vector whose components are the mean values of each feature:
(3)
Hence we need to compute the eigenvectors of the covariance matrix
and sort them so that the corresponding eigenvalues
are sorted in descending order, i.e.:
(4)
Finally, the compression matrix of PCA can be expressed as:
(5)
The eigenvectors of the covariance matrix are called principal components.
The eigenvalue represents the variance of the data along the direction of the corresponding principal component. Hence the components with the lowest eigenvalues contain the least information, so they can be dropped. The importance of each component is represented by the so-called explained variance ratio, which indicates the portion of the variance that lies along each principal component:
(6)
Note that sum at the denominator is performed over the maximum number of principal components.
By summing the explained variance ratio of the first components, we obtain the so-called cumulative explained variance:
(7)
A good strategy is to choose the number of dimensions for which the cumulative explained variance exceeds a threshold, e.g., 0.95 (95%).
Let’s now apply the PCA to the MNIST dataset by exploiting the implementation provided in the Python package scikit-learn.
We load the MNIST dataset using a keras function, and we normalize the training set in the range :
import numpy as np
from keras.datasets import mnist
(x_train, y_train), (x_test, y_test) = mnist.load_data()
x_train = x_train.reshape(-1, 28*28) / 255.0We perform the PCA on the training set by considering all principal components (), and then we compute the cumulative explained variance for each number of dimension:
from sklearn.decomposition import PCA
pca = PCA()
pca.fit(x_train)
cumsum = np.cumsum(pca.explained_variance_ratio_)Looking at the plot of the explained variance as a function of the number of principal components, we observe an elbow in the curve. The optimal number of principal components is reached when the cumulative variance stops growing fast:
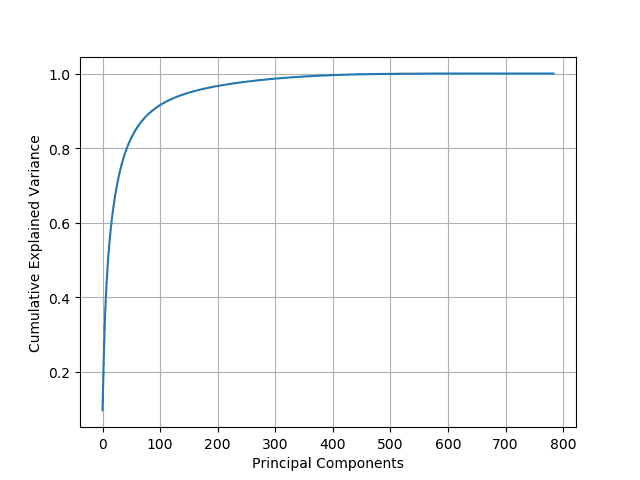
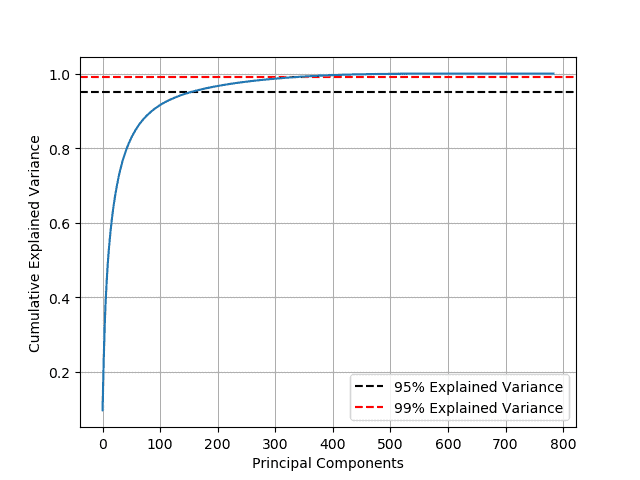
The minimum number of principal components required to preserve the 95% of the data’s variance can be computed with the following command:
d = np.argmax(cumsum >= 0.95) + 1
We found that the number of dimensions can be reduced from 784 to 150 while preserving 95% of its variance. Hence, the compressed dataset is now 19% of its original size! If we want to preserve 99% of the variance, the number of dimensions can be reduced to 330, i.e., 42% of the original size:
In this article, we reviewed the Principal Component Analysis, a popular dimensionality reduction technique. Then, we described how to use it by choosing the optimal number of principal components. Finally, we showed the application of the PCA to the MNIST dataset using a Python implementation.