1. Overview
In this tutorial, we’ll talk about the “Curse of Dimensionality” (CoD), a phenomenon frequently addressed in machine learning. First, we’ll explain this concept with a simple argument. Then we’ll discuss how to overcome the CoD.
2. What Is the Curse of Dimensionality?
The CoD refers to a set of phenomena that occur when analyzing data in a high-dimensional space. The term was introduced in 1957 by the mathematician Richard E. Bellman to describe the increased volume observed when adding extra dimensions to Euclidean space.
In machine learning, the number of features corresponds to the dimension of the space in which the data are represented. A high-dimensional dataset contains a number of features of the order of a hundred or more. When the dimensionality increases, the volume of the space increases, and the data become more sparse.
A higher number of features increase the training time but also affects the performance of a classifier. In fact, when we have too many features, it is much harder to cluster the data and identify patterns. In a high-dimensional space, training instances are sparse, and new instances are likely far away from the training instances. In other words, the more features the training dataset has, the greater the risk of overfitting our model.
Such difficulties in training models with high dimensional data are referred to as the “Curse of Dimensionality”.
3. Hughes Phenomenon
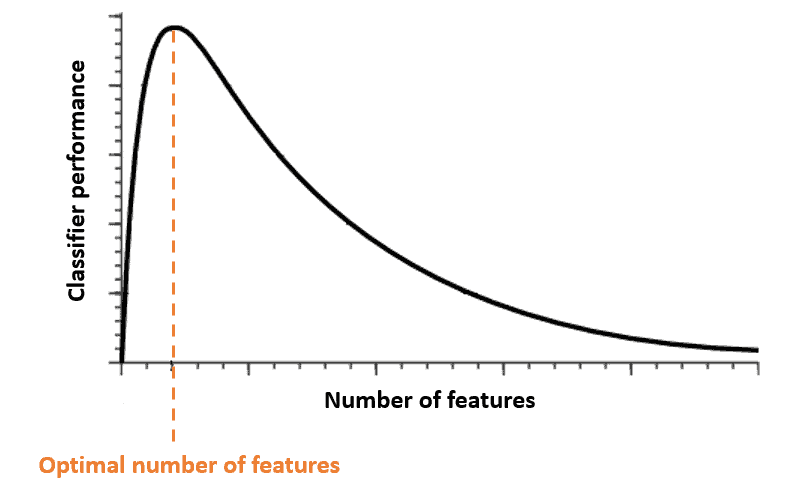
The CoD is closely related to the Hughes Phenomenon. It states that with a fixed number of training instances, the performance of a classifier first increases as the number of features increases until we reach the optimal number of features. Adding more features beyond this value will deteriorate the classifier’s performance:
4. How to Overcome the CoD?
In theory, a solution to the CoD could be to enhance the density of data by increasing the number of training instances. In practice, it is hard to do. In fact, the number of training observations required to obtain a given density increases exponentially with the number of features.
Dimensionality reduction techniques are effective solutions to the CoD. These techniques can be divided into two categories: feature selection and feature extraction.
4.1. Feature Selection Techniques
Feature selection techniques try to select the features that are more relevant and remove the irrelevant ones. The most commonly used feature selection techniques are discussed below.
- Low Variance filter: in this technique, the variance of each feature is computed over the training set. The features with low variance are eliminated. Such features will assume almost a constant value. Therefore they have no discriminating power.
- High Correlation filter: the technique computes the pair-wise correlation between features. If a high correlation is observed for a pair of features, one of them is eliminated, and the other one retained.
- Feature Ranking: in this case, Decision Trees models are used to rank the features according to their contribution to the model predictability. Lower ranked attributes are eliminated.
4.2. Feature Extraction Techniques
Feature extraction techniques transform the data from the high-dimensional space to a representation with fewer dimensions. Unlike the feature selection techniques, the feature extraction approach creates new features from functions of the original ones. The most commonly used feature extraction techniques are discussed below.
Principal Component Analysis (PCA) is the most popular dimensionality reduction technique. It finds the linear transformations for which the mean squared error computed over a set of instances is minimal. The column vectors of the matrix representing this linear transformation are called principal components. Original data are projected along with the principal components with the highest variance. Hence, the data are transformed to a lower dimensionality that captures most of the information of the original dataset.
Linear Discriminant Analysis (LDA) finds the linear transformation that minimizes the inter-class variability and maximizes the separation between the classes. Unlike the PCA, the LDA requires labeled data.
5. Conclusion
In this article, we reviewed the problems related to the “Curse of Dimensionality” in machine learning. Finally, we illustrated the techniques to solve them.