1. Introduction
In this tutorial, we’ll investigate how to split a dataset into training and test sets.
Firstly, we’ll try to understand why do we split the dataset. Then, we’ll learn about finding a good split ratio for our dataset.
2. Why Split the Dataset?
To detect a machine learning model behavior, we need to use observations that aren’t used in the training process. Otherwise, the evaluation of the model would be biased.
Using the training observations for model evaluation is like giving a class of students a set of questions, then asking some of the questions in the final exam. We can’t know whether the pupils really learned the subject or just memorized some specific data.
The simplest method is to divide the whole dataset into two sets. Then use one for training and the other for model evaluation. This is called the holdout method.
Let’s have a look at the meanings of data subsets first:

We train the machine learning models using these observations. In other words, we feed these observations into the model to update its parameters during the learning phase.
We test the machine learning model after the training phase is complete, using the observations from the test set. This way, we measure how the model reacts to new observations. Train and test sets should follow the same distribution.
Using the holdout method reduces the risk of possible issues such as data leaking or overfitting. Hence, we ensure that the trained model generalizes well on new data.
3. How to Split the Dataset?
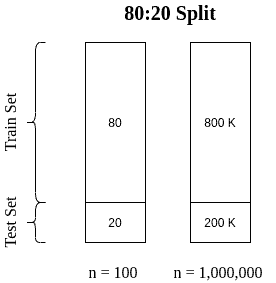
If we search the Internet for the best train-test ratio, the first answer to pop will be 80:20. This means we use 80% of the observations for training and the rest for testing. Older sources and some textbooks would tell us to use a 70:30 or even a 50:50 split. On the contrary, sources on deep learning or big data would suggest a 99:1 split.
Like all machine learning problems, this question doesn’t have one simple answer. With less training data, the parameter estimates have a high variance. On the other hand, less testing data leads to high variance in performance measures.
The dataset size implies a split ratio. Obviously, using the same ratio on datasets with different sizes results in varying train and test set sizes:
If the dataset is relatively small (n < 10,000), 70:30 would be a suitable choice.
However, for smaller datasets (n < 1,000), each observation is extremely valuable, and we can’t spare any for validation. In this case, k-fold cross-validation is a better choice than the holdout method. This method is computationally expensive. Yet it offers an effective model evaluation over a small dataset by training multiple models.
On the contrary, a very large dataset (like millions of observations) gives us flexibility. We can choose a high split ratio like 99:1 or even higher:
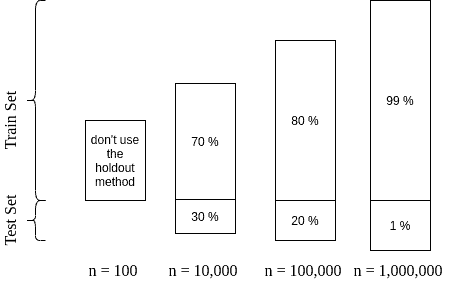
With datasets containing considerably high observations, 80:20 is a good starting point. Overall, we need to make sure that the test set represents most of the variance in the dataset. We can ensure this by trying different amounts of test data.
For example, we start with an 80:20 split. Then, we train a model using 80% of the dataset. By using portions of the test data (100%, 70%, 50%, etc.), we can see if a smaller test set can cover the variance. Having a smaller portion performing similar to the whole test set proves it’s covered. Otherwise, we can consider using a larger test set.
4. Conclusion
In this article, we’ve learned about the holdout method and splitting our dataset into train and test sets.
Unfortunately, there’s no single rule of thumb to use. So, depending on the size of the dataset, we need to adopt a different split ratio.