Attention vs. Self-Attention

Last updated: March 19, 2024

1. Introduction

A core component of Large Language models is the Transformer block. A core component of the Transformer block is the Attention mechanism. Attention comes in many flavors and set-ups for specific uses. The flavors and variations of attention reflect its development history. In many cases, history, associated jargon, and naming distinctions make it harder to understand the core concepts.

In this tutorial, we cover and distinguish the two main flavors and uses of attention. These are Attention and Self-Attention. These common terms are at the core of recurrent encoder-decoder and transformer architectures. We cover their context and utility within that pipeline and highlight their distinctions.

2. Attention

Attention attempts to solve a problem when recurrently processing a sequence of inputs. In a traditional recurrent encoder-decoder architecture, a history term, the encoder context, is maintained and added or appended to each input vector of the decoder. Therefore, this very simple method of preserving a history record fails to achieve long-term memory and reconstructive power. There is too much information to encode, and data gets lost.

The attention mechanism solves the problem of understanding what is important in a potentially very long sequence of data. Since this can change depending on the input, it is obvious that we require a dynamic system.

3. Badhanau Attention

The solution to fitting a variable-length sequence into a fixed-length vector is to add a step. The (Badhanau) attention mechanism generates a context vector for each part of a sequence. Then, it computes a weighted sum dynamically over those context vectors to create a new context vector for each input to the decoder. This weighted sum over context vectors is (Badhanau) attention.

This idea, also known as additive attention, was powerful, and many variants exist as possible extensions and improvements. This leads to Self-Attention or dot-product attention.

First, we’ll cover Badhanau’s technical details. Dimitry Badhanau proposed the Badhanau Attention as part of an encoder-decoder paradigm. The encoder E is a standard bi-directional RNN. This architecture constructs a hidden representation for each sequence element. When decoding, we use each of these encodings to build a context for the decoder. As a result, we call the method by which we combine these encodings attention:

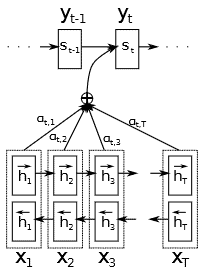
Badhanau Attention Architecture Example

3.1. Technical Details: the Decoder

The decoder takes the previous token, the hidden state, and the context from the encoder as inputs and produces the next token. Additionally, what sets the Badhanau decoder apart from contemporary approaches is that the context vector fed to the decoder is now a dynamic combination of the encoders’ encodings and not a static single encoding of the entire sequence.

The decoder’s previous hidden state is passed through an alignment module for each encoder output vector. A softmax is computed over the outputs to discern which encoder state is most aligned with the current decoder state. The softmax values are weights to calculate a weighted sum over the encoder outputs. This produces a context vector for the current decoder state. Then, this context is found to be used to create the next decoder output.

We can define the Decoder context per input as:

(1)   \begin{equation*} c_i = \sum_{i}^{T} \alpha_{i,t}h_i \end{equation*}

Where h_i is the hidden state encoding for the encoder and \alpha is the computed softmax weight for that particular hidden encoder state, the attention.

The attention \alpha is computed with each of the encoders hidden states combined with the current hidden state of the decoder.

(2)   \begin{equation*} e_{t,i} = a(s_{t-1},h_i) \end{equation*}

We compute \alpha as :

(3)   \begin{equation*} \alpha_{I,t} = softmax(e_{t,I}) \end{equation*}

Finally, we also define the attention function computation as follows

(4)   \begin{equation*} a(s_{t-1},h_i) = v^TtanH(W[h_i ; s_{t-1}]) \end{equation*}

Where v and W are learnable weight vectors and matrices, respectively. We can split the multiplication with W into two computations with h_i and s_{t-1} separately and added together or as one larger multiplication as shown.

4. Self-Attention

First, self-attention builds on the idea of attention in what is a compelling way. It eschews the idea of recurrence, allowing its computations along a sequence to be computed in parallel rather than sequentially. Self-attention is a key innovation enabling the transformer architecture, which has succeeded in progressing natural language tasks.

Self-attention builds on the same basic concept as Badhanau’s attention. The goal is to compute a weight vector across tokenwise sentence embeddings to discern which sentence elements are the most important.

Generally, we have said that self-attention runs in parallel, and recurrence does not limit it. A sequence encoding is constructed and appended to each input token to achieve that and maintain sequence information. There are a variety of implementations of this. The standard approach combines Sine and Cosine functions to produce a unique positional embedding. This, however, is still not a free lunch, and abandoning recurrence also forces us to use fixed-length windows, known as context length, over the sequence.

4.1. Technical Details

The attention mechanism for a given input sequence computes a query, key, and value matrix via linear transformations. Moreover, the dot-product between the query and key matrices is used to compute a score for each input word or token with each token in the sequence. The softmax turns this score into a normalized weighting over every other vector in the sequence. In brief, this weighting is our attention score. Furthermore, we use it to multiply with the value matrix to produce our attended sequence output. The given equation summarises the process:

(5)   \begin{equation*} Attention(Q,K,V) = softmax(\frac{QK^T}{\sqrt{d_k}})V \end{equation*}

The division by \sqrt{d_k} is a scaling factor introduced in attention is all you need, extending the existing dot-product attention to produce scaled-dot-product attention. This scaling helps to reduce the impact of large dimensional multiplications, creating small gradients via the softmax operation.

Finally, the diagram visualizes the whole procedure:

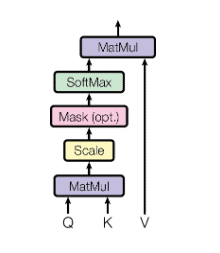
a diagram of the compute steps for Scaled Dot-Product Attention

5. Differences

To sum up, attention and self-attention are similar in that they construct a weighted vector that acts as an importance or attention score on the elements of a sequence. Self-attention, however, acts internally on the input sequence.

In conclusion, the key differences are

Attention Self-Attention
Context We typically use Bahdanau attention in sequence-to-sequence models, focusing on aligning and translating sequences. Self-attention is a more general mechanism for capturing relationships within a sequence. It is used in various architectures, especially in transformer models.
Learned Parameters Bahdanau attention involves learning parameters for the alignment model, making it more complex in terms of the number of parameters. Self-attention relies on dot products and scaling, and the attention weights are solely based on the input sequence without additional learned parameters for alignment.

6. Conclusion

In this article, we highlighted the distinctions between Badhanau Attention and Self-Attention. Thus, we clearly provided a deep dive into the inner workings of the attention mechanism and its developmental history.

In summary, attention is a fundamental concept in understanding the functioning and training complexity of large language models. Understanding the history and context of these developments can also provide insight into their function and utility.

Comments are open for 30 days after publishing a post. For any issues past this date, use the Contact form on the site.