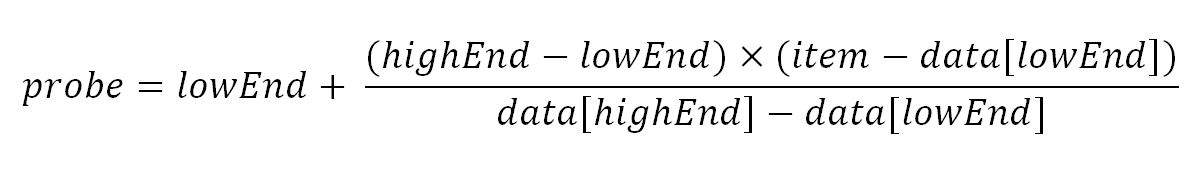Interpolation Search in Java

1. Introduction

In this tutorial, we’ll walk through interpolation search algorithms and discuss their pros and cons. Furthermore, we’ll implement it in Java and talk about the algorithm’s time complexity.

2. Motivation

Interpolation search is an improvement over binary search tailored for uniformly distributed data.

Binary search halves the search space on each step regardless of the data distribution, thus it’s time complexity is always O(log(n)).

On the other hand, interpolation search time complexity varies depending on the data distribution. It is faster than binary search for uniformly distributed data with the time complexity of O(log(log(n))). However, in the worst-case scenario, it can perform as poor as O(n).

3. Interpolation Search

Similar to binary search, interpolation search can only work on a sorted array. It places a probe in a calculated position on each iteration. If the probe is right on the item we are looking for, the position will be returned; otherwise, the search space will be limited to either the right or the left side of the probe.

The probe position calculation is the only difference between binary search and interpolation search.

In binary search, the probe position is always the middlemost item of the remaining search space.

In contrary, interpolation search computes the probe position based on this formula:

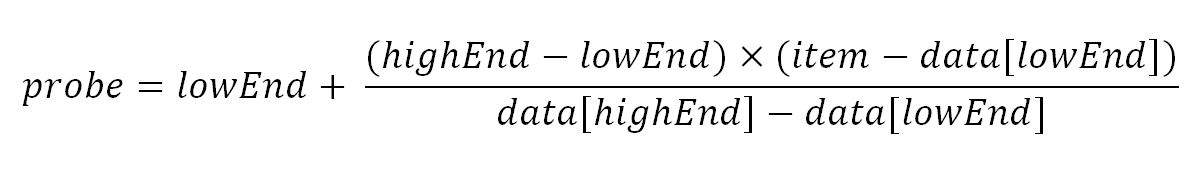
Let’s take a look at each of the terms:

• probe: the new probe position will be assigned to this parameter.
• lowEnd: the index of the leftmost item in the current search space.
• highEnd: the index of the rightmost item in the current search space.
• data[]: the array containing the original search space.
• item: the item that we are looking for.

To better understand how interpolation search works, let’s demonstrate it with an example.

Let’s say we want to find the position of 84 in the array below:

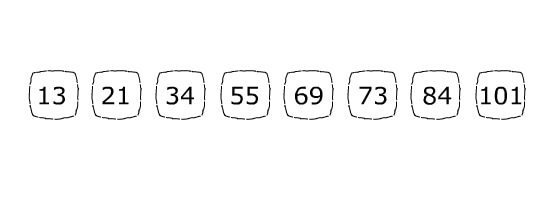
The array’s length is 8, so initially highEnd = 7 and lowEnd = 0 (because array’s index starts from 0, not 1).

In the first step, the probe position formula will result in probe = 5:

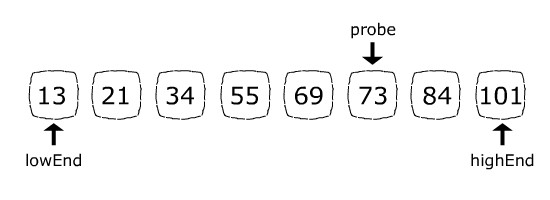
Because 84 (the item we are looking for) is greater than 73 (the current probe position item), the next step will abandon the left side of the array by assigning lowEnd = probe + 1. Now the search space consists of only 84 and 101. The probe position formula will set probe = 6 which is exactly the 84’s index:

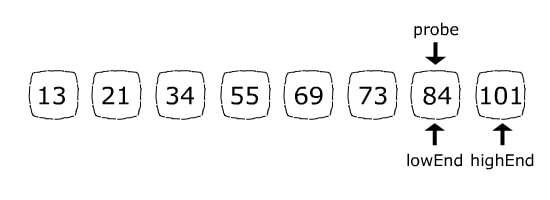
Since the item we were looking for is found, position 6 will be returned.

4. Implementation in Java

Now that we understood how the algorithm works, let’s implement it in Java.

First, we initialize lowEnd and highEnd:

int highEnd = (data.length - 1);
int lowEnd = 0;

Next, we set up a loop and in each iteration, we calculate the new probe based on the aforementioned formula. The loop condition makes sure that we are not out of the search space by comparing item to data[lowEnd] and data[highEnd]:

while (item >= data[lowEnd] && item <= data[highEnd] && lowEnd <= highEnd) {
    int probe
      = lowEnd + (highEnd - lowEnd) * (item - data[lowEnd]) / (data[highEnd] - data[lowEnd]);
}

We also check if we’ve found the item after every new probe assignment.

Finally, we adjust lowEnd or highEnd to decrease the search space on each iteration:

public int interpolationSearch(int[] data, int item) {

    int highEnd = (data.length - 1);
    int lowEnd = 0;

    while (item >= data[lowEnd] && item <= data[highEnd] && lowEnd <= highEnd) {

        int probe
          = lowEnd + (highEnd - lowEnd) * (item - data[lowEnd]) / (data[highEnd] - data[lowEnd]);

        if (highEnd == lowEnd) {
            if (data[lowEnd] == item) {
                return lowEnd;
            } else {
                return -1;
            }
        }

        if (data[probe] == item) {
            return probe;
        }

        if (data[probe] < item) {
            lowEnd = probe + 1;
        } else {
            highEnd = probe - 1;
        }
    }
    return -1;
}

5. Conclusion

In this article, we explored the interpolation search with an example. We implemented it in Java, too.