Guide to In-Place Sorting Algorithm Works with a Java Implementation

Last updated: January 25, 2024

Written by: baeldung

Reviewed by: Michal Aibin

Algorithms

Sorting

Modern software architecture is often broken. Slow delivery leads to missed opportunities, innovation is stalled due to architectural complexities, and engineering resources are exceedingly expensive.

Orkes is the leading workflow orchestration platform built to enable teams to transform the way they develop, connect, and deploy applications, microservices, AI agents, and more.

With Orkes Conductor managed through Orkes Cloud, developers can focus on building mission critical applications without worrying about infrastructure maintenance to meet goals and, simply put, taking new products live faster and reducing total cost of ownership.

Try a 14-Day Free Trial of Orkes Conductor today.

Orkes is the leading workflow orchestration platform built to enable teams to transform the way they develop, connect, and deploy applications, microservices, AI agents, and more.

Try a 14-Day Free Trial of Orkes Conductor today.

Orkes is the leading workflow orchestration platform built to enable teams to transform the way they develop, connect, and deploy applications, microservices, AI agents, and more.

Try a 14-Day Free Trial of Orkes Conductor today.

Refactor Java code safely — and automatically — with OpenRewrite.

Refactoring big codebases by hand is slow, risky, and easy to put off. That’s where OpenRewrite comes in. The open-source framework for large-scale, automated code transformations helps teams modernize safely and consistently.

Each month, the creators and maintainers of OpenRewrite at Moderne run live, hands-on training sessions — one for newcomers and one for experienced users. You’ll see how recipes work, how to apply them across projects, and how to modernize code with confidence.

Join the next session, bring your questions, and learn how to automate the kind of work that usually eats your sprint time.

1. Introduction

In this tutorial, we’ll explain how the in-place sorting algorithm works.

2. In-Place Algorithms

The in-place algorithms are those that don’t need any auxiliary data structure in order to transform the input data. Basically, it means that the algorithm doesn’t use extra space for input manipulation. It practically overrides the input with the output.

However, in reality, the algorithm actually may require a small and non-constant additional space for auxiliary variables. The complexity of this space is in most cases O(log n), although sometimes anything less than linear is allowed.

3. Pseudocode

Let’s now see some pseudocode and compare the in-place algorithm with the out-of-place one.

We’ll assume that we want to reverse an array of n numbers.

3.1. In-Place Algorithm

If we think about the problem, we’ll see that we have an input array and reversed array as the output. In the end, we don’t actually need our original array, only the reversed one.

Then, why wouldn’t we overwrite the input instead of moving its values to the completely new array, as it might look like a most obvious method? To do that, we’ll only need one additional variable to temporarily store the values that we’re currently working with:

reversInPlace(array A[n])
    for i from 0 to n/2
    temp = A[i]
    A[i] = A[n - 1 - i]
    A[n - 1 - i] = temp

It’s noteworthy to mention that no matter how big the array is, the extra space that we need will always be O(1) in this case.

The illustration shows that we need fewer steps than in the previous case:

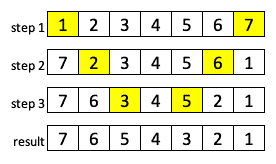
3.2. Out-of-Place Algorithm

On the other hand, we can also do this in a pretty simple, more obvious manner. We can create a new array of the same size, copy the values from the original one in the corresponding order and then delete the original array:

reverseOutOfPlace(array A[n])
    create new array B[n]
    for i from 0 to n - 1
        B[i] = A[i]
    delete A
    return B

Although this will do what we wanted it to do, it’s not efficient enough. We have O(n) extra space required since we have two arrays to manipulate with. Besides that, creating and removing a new array is usually a slow operation.

Let’s see the illustration of the process:

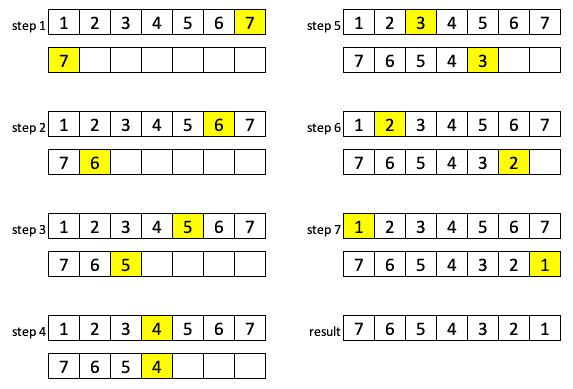
4. Java Implementation

Let’s now see how we can implement in Java what we learned in the previous section.

Firstly, we’ll implement an in-place algorithm:

public static int[] reverseInPlace(int A[]) {
    int n = A.length;
    for (int i = 0; i < n / 2; i++) {
        int temp = A[i];
        A[i] = A[n - 1 - i];
        A[n - 1 - i] = temp;
    }
    return A;
}

We can test easily that this works as expected:

@Test
void givenArray_whenInPlaceSort_thenReversed() {
    int[] input = {1, 2, 3, 4, 5, 6, 7};
    int[] expected = {7, 6, 5, 4, 3, 2, 1};
    assertArrayEquals("the two arrays are not equal", expected,
      InOutSort.reverseInPlace(input));
}

Secondly, let’s check out the out-of-place algorithm implementation:

public static int[] reverseOutOfPlace(int A[]) {
    int n = A.length;
    int[] B = new int[n];
    for (int i = 0; i < n; i++) {
        B[n - i - 1] = A[i];
    }
    return B;
}

The test is pretty straightforward:

@Test
void givenArray_whenOutOfPlaceSort_thenReversed() {
    int[] input = {1, 2, 3, 4, 5, 6, 7};
    int[] expected = {7, 6, 5, 4, 3, 2, 1};
    assertArrayEquals("the two arrays are not equal", expected,
      InOutSort.reverseOutOfPlace(input));
}

5. Examples

There are many sorting algorithms that are using in-place approach. Some of them are insertion sort, bubble sort, heap sort, quicksort, and shell sort and you can learn more about them and check-out their Java implementations.

Also, we need to mention comb sort and heapsort. All these have space complexity O(log n).

It could be also useful to learn more about the Theory of Big-O Notation, as well as to check out some Practical Java Examples about the complexity of the algorithm.

6. Conclusion

In this article, we described the so-called in-place algorithms, illustrated how they work using pseudocode and a few examples, listed several algorithms that work on this principle, and finally implemented the basic examples in Java.

The code backing this article is available on GitHub. Once you're logged in as a Baeldung Pro Member, start learning and coding on the project.

Orkes is the leading workflow orchestration platform built to enable teams to transform the way they develop, connect, and deploy applications, microservices, AI agents, and more.

Try a 14-Day Free Trial of Orkes Conductor today.

Orkes is the leading workflow orchestration platform built to enable teams to transform the way they develop, connect, and deploy applications, microservices, AI agents, and more.

Try a 14-Day Free Trial of Orkes Conductor today.

Modern Java teams move fast — but codebases don’t always keep up. Frameworks change, dependencies drift, and tech debt builds until it starts to drag on delivery. OpenRewrite was built to fix that: an open-source refactoring engine that automates repetitive code changes while keeping developer intent intact.

The monthly training series, led by the creators and maintainers of OpenRewrite at Moderne, walks through real-world migrations and modernization patterns. Whether you’re new to recipes or ready to write your own, you’ll learn practical ways to refactor safely and at scale.

If you’ve ever wished refactoring felt as natural — and as fast — as writing code, this is a good place to start.