1. Introduction
In this tutorial, we’ll describe the Shell sort algorithm in Java.
2. The Shell Sort Overview
2.1. Description
Let’s first describe the Shell sort algorithm so we know what we’re trying to implement.
Shell sort is based on the Insertion sorting algorithm, and it belongs to the group of very efficient algorithms. In general, the algorithm breaks an original set into smaller subsets and then each of those is sorted using Insertion sort.
But, how it makes the subsets is not straightforward. It doesn’t choose neighboring elements to form a subset as we might expect. Rather, shell sort uses the so-called interval or gap for subset creation. For example, if we have the gap I, it means that one subset will contain the elements that are I positions apart.
Firstly, the algorithm sorts the elements that are far away from each other. Then, the gap becomes smaller and closer elements are compared. This way, some elements that aren’t in a correct position can be positioned faster than if we made the subsets out of the neighboring elements.
2.2. An Example
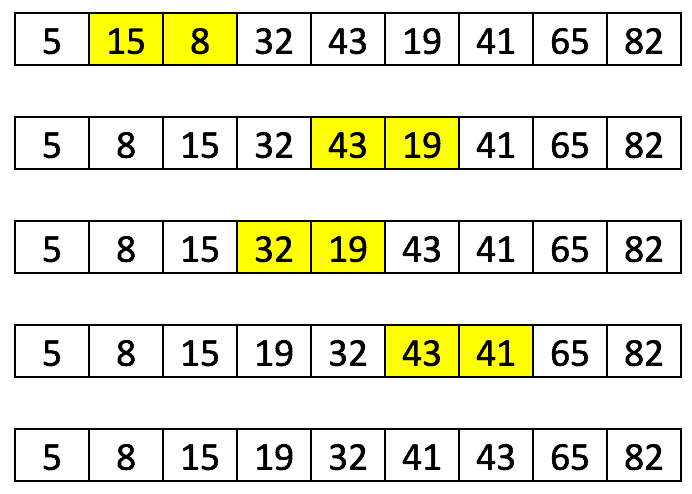
Let’s see this in the example with the gaps of 3 and 1 and the unsorted list of 9 elements:

If we follow the above description, in the first iteration, we’ll have three subsets with 3 elements (highlighted by the same color):

After sorting each of the subsets in the first iteration, the list would look like:

We can note that, although we don’t have a sorted list yet, the elements are now closer to desired positions.
Finally, we need to do one more sort with the increment of one and it’s actually a basic insertion sort. The number of shifting operations that we need to perform to sort a list is now smaller than it would be the case if we didn’t do the first iteration:
2.3. Choosing the Gap Sequences
As we mentioned, the shell sort has a unique way of choosing gap sequences. This is a difficult task and we should be careful not to choose too few or too many gaps. More details can be found in the most proposed gap sequences listing.
3. Implementation
Let’s now take a look at the implementation. We’ll use Shell’s original sequence for interval increments:
N/2, N/4, …, 1 (continuously dividing by 2)
The implementation itself is not too complex:
public void sort(int arrayToSort[]) {
int n = arrayToSort.length;
for (int gap = n / 2; gap > 0; gap /= 2) {
for (int i = gap; i < n; i++) {
int key = arrayToSort[i];
int j = i;
while (j >= gap && arrayToSort[j - gap] > key) {
arrayToSort[j] = arrayToSort[j - gap];
j -= gap;
}
arrayToSort[j] = key;
}
}
}
We first created a gap sequence with a for loop and then did the insertion sort for each gap size.
Now, we can easily test our method:
@Test
void givenUnsortedArray_whenShellSort_thenSortedAsc() {
int[] input = {41, 15, 82, 5, 65, 19, 32, 43, 8};
ShellSort.sort(input);
int[] expected = {5, 8, 15, 19, 32, 41, 43, 65, 82};
assertArrayEquals("the two arrays are not equal", expected, input);
}
4. Complexity
Generally, the Shell sort algorithm is very efficient with medium-sized lists. The complexity is difficult to determine since it depends a lot on the gap sequence, but the time complexity varies between O(N) and O(N^2).
The worst-case space complexity is O(N) with O(1) auxiliary space.
5. Conclusion
In this tutorial, we described Shell sort and illustrated how we can implement it in Java.
As usual, the entire code could be found over on GitHub.









