1. Overview
When working with 2D geometry, one common problem is to determine whether a point lies between two other points on a straight line.
In this quick tutorial, we’ll explore different approaches to making this determination in Java.
2. Understanding the Problem Statement
Let’s say we’ve two points on a plane: the first point A has the coordinates (x1, y1), and the second point B has the coordinates (x2, y2). We want to check whether a given point C with (x3,y3) coordinates lies between A and B or not:
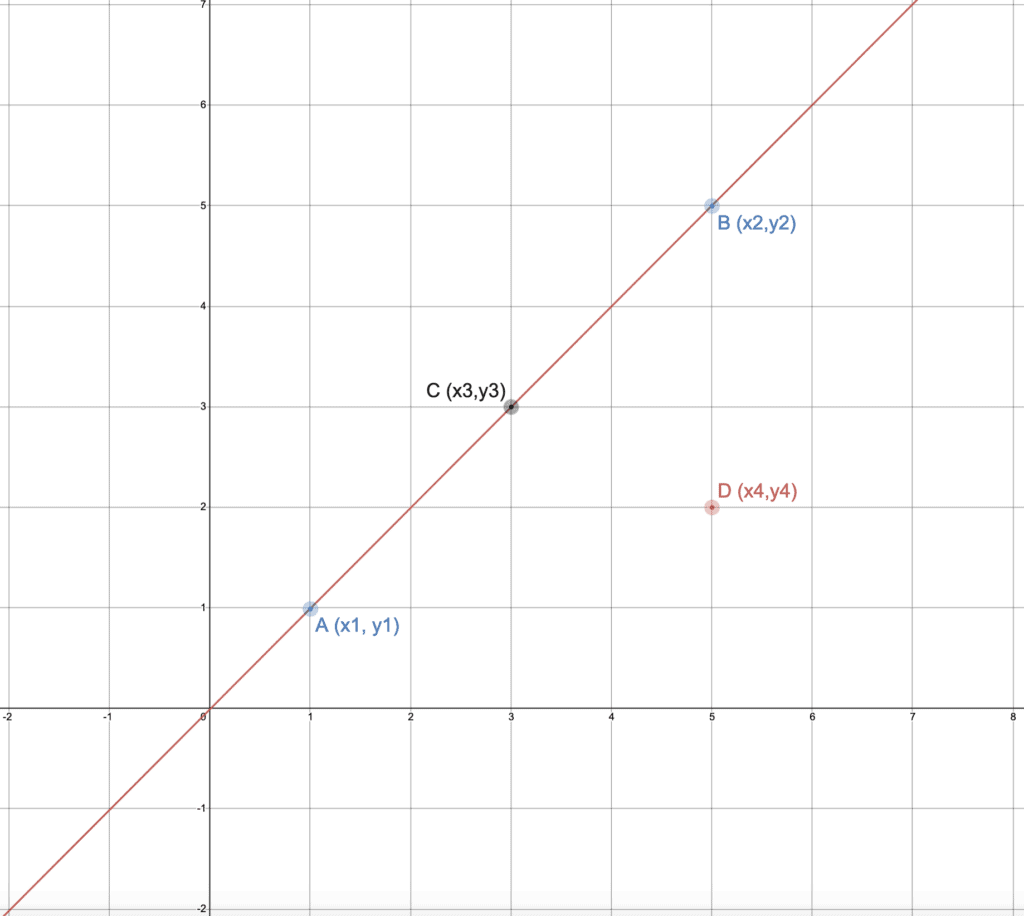
In the above graph, point C lies between points A and B, whereas point D does not lie between points A and B.
This approach involves calculating the distances: AC, CB, and AB from point A to C, point C to B, and point A to B, respectively. If C lies between points A and B, then the sum of AC and CB will be equal to AB:
distance (AC) + distance (CB) == distance (AB)
We can use the distance formula to calculate the distance between two different points. If point A has the coordinates (x1, y1), and point B has the coordinates (x2, y2), then we can calculate the distance by using the formula:
distance = sqrt((y2 - y1) * (y2 - y1) + (x2 - x1) * (x2 - x1))
Let’s use the distance formula on the above diagram to verify the approach:
Distance from point A (1,1) to point B (5,5) = 5.656
Distance from point A (1,1) to point C (3,3) = 2.828
Distance from point C (3,3) to point B (5,5) = 2.828
Here, distance (AC) + distance (CB) = 5.656, which is equal to distance (AB). It shows that point C lies between point A and point B.
Let’s use the distance formula to check whether a point lies between two points or not:
boolean isPointBetweenTwoPoints(double x1, double y1, double x2, double y2, double x, double y) {
double distanceAC = Math.sqrt(Math.pow(x - x1, 2) + Math.pow(y - y1, 2));
double distanceCB = Math.sqrt(Math.pow(x2 - x,2) + Math.pow(y2 - y, 2));
double distanceAB = Math.sqrt(Math.pow(x2 - x1,2) + Math.pow(y2 - y1, 2));
return Math.abs(distanceAC + distanceCB - distanceAB) < 1e-9;
}
Here, 1e-9 is a small eplison value used to account for rounding errors and imprecisions that can occur in floating-point calculations. If the absolute difference is very small (less than 1e-9), we’ll consider it as equality.
Let’s test this approach using the above values:
void givenAPoint_whenUsingDistanceFormula_thenCheckItLiesBetweenTwoPoints() {
double x1 = 1;<br /> double y1 = 1;<br />
double x2 = 5;<br /> double y2 = 5;<br />
double x = 3;<br /> double y = 3;
<br /> assertTrue(findUsingDistanceFormula(x1, y1, x2, y2, x, y));
}
In this approach, we’ll be calculating the slope of the lines AB and AC using the slope formula. We’ll compare these slopes to check the collinearity, i.e., the slope of AB and AC are equal. It will help us determine whether points A, B, and C are aligned or not.
If point A has the coordinates (x1, y1), and point B has the coordinates (x2, y2), then we can calculate the slope by using the formula:
slope = (y2 - y1) / (x2 - x1)
If the slopes of AB and AC are equal, and point C lies within the x and y coordinate range defined by A and B points, we can say that point C lies between point A and point B.
Let’s calculate the slope of AB and AC on the above diagram to verify the approach:
Slope of AB = 1.0
Slope of AC = 1.0
Point C is (3,3)
Here, AB = AC, and Point C’s x and y coordinates lie between the range defined by A (1,1) and B (5,5), which shows that point C lies between point A and point B.
Let’s use this approach to check whether a point lies between two points or not:
boolean findUsingSlopeFormula(double x1, double y1, double x2, double y2, double x, double y) {
double slopeAB = (y2 - y1) / (x2 - x1);
double slopeAC = (y - y1) / (x - x1);
return slopeAB == slopeAC && ((x1 <= x && x <= x2) || (x2 <= x && x <= x1)) && ((y1 <= y && y <= y2) || (y2 <= y && y <= y1));
}
Let’s test this approach using the above values:
void givenAPoint_whenUsingSlopeFormula_thenCheckItLiesBetweenTwoPoints() {
double x1 = 1;<br /> double y1 = 1;<br />
double x2 = 5;<br /> double y2 = 5;<br />
double x = 3;<br /> double y = 3;
<br /> assertTrue(findUsingSlopeFormula(x1, y1, x2, y2, x, y));
}
5. Conclusion
In this tutorial, we’ve discussed ways to determine whether a point lies between two other points on a straight line.
As always, the code used in the examples is available over on GitHub.





