1. Introduction
Java provides some primitives, such as int or long, to perform integer operations. But sometimes, we need to store numbers, which overflow the available limits for those data types.
In this tutorial, we’ll look deeper into the BigInteger class. We’ll check its structure by looking into the source code and answer the question – how is it possible to store large numbers outside the limit of available primitive data types?
2. BigInteger Class
As we know, the BigInteger class is used for mathematical operations which involve very big integer calculations larger than the primitive long type. It represents immutable arbitrary-precision integers.
Before going further, let’s remember that in Java all bytes are represented in the two’s-complement system using the big-endian notation. It stores the most significant byte of a word at the smallest memory address (the lowest index). Moreover, the first bit of the byte is also a sign bit. Let’s inspect example byte values:
- 1000 0000 represents -128
- 0111 1111 represents 127
- 1111 1111 represents -1
So now, let’s check the source code and explain how it stores given numbers exceeding available primitives limits.
2.1. int signum
The signum property determines the sign of the BigInteger. Three integer values represent the value’s sign: -1 for negative, 0 for zero, 1 for positive numbers:
assertEquals(1, BigInteger.TEN.signum());
assertEquals(-1, BigInteger.TEN.negate().signum());
assertEquals(0, BigInteger.ZERO.signum());
Let’s be aware that BigInteger.ZERO must have the signum of 0 due to the magnitude array. This value ensures that there is exactly one representation for each BigInteger value.
2.2. int[] mag
All the magic of the BigInteger class starts with the mag property. It stores the given value in an array using the binary representation, which allows omitting primitive data types limits.
Moreover, the BigInteger groups them in 32-bit portions – a set of four bytes. Due to this, the magnitude inside the class definition is declared as the int array:
int[] mag;
This array holds the magnitude of the given value in big-endian notation. The zeroth element of this array is the most significant int of the magnitude. Let’s check it using BigInteger(byte[] bytes):
assertEquals(new BigInteger("1"), new BigInteger(new byte[]{0b1}))
assertEquals(new BigInteger("2"), new BigInteger(new byte[]{0b10}))
assertEquals(new BigInteger("4"), new BigInteger(new byte[]{0b100}))
This constructor translates a given byte array containing the two’s-complement binary representation into the value.
Since there’s a sign-magnitude variable (signum), we don’t use the first bit as a sign bit of the value. Let’s quickly check it:
byte[] bytes = { -128 }; // 1000 0000
assertEquals(new BigInteger("128"), new BigInteger(1, bytes));
assertEquals(new BigInteger("-128"), new BigInteger(-1, bytes));
We created two different values using the BigInteger(int signum, byte[] magnitude) constructor. It translates the sign-magnitude representation into the BigInteger. We reused the same bytes array, changing only a sign value.
We can also print the magnitude using the toString(int radix) method:
assertEquals("10000000", new BigInteger(1, bytes));
assertEquals("-10000000", new BigInteger(-1, bytes));
Notice that for the negative values, the minus sign is added.
Finally, the magnitude’s most significant int must be non-zero. This implies that the BigInteger.ZERO has a zero-length mag array:
assertEquals(0, BigInteger.ZERO.bitCount());
assertEquals(BigInteger.ZERO, new BigInteger(0, new byte[]{}));
For now, we’ll skip inspecting other properties. They are marked as deprecated due to redundancy, used only as internal cache.
Let’s now go straight to the more complex examples and check how the BigInteger stores numbers over the primitive data types.
3. BigInteger Larger Than Long.MAX_VALUE.
As we already know, the long data type is a 64-bit two’s complement integer. The signed long has a minimum value of -263 (1000 0000 … 0000) and a maximum value of 263-1 (0111 1111 … 1111). To create a number over those limits, we need to use the BigInteger class.
Let’s now create a value larger by one than Long.MAX_VALUE, equal to 263. According to the information in the previous chapter, it needs to have:
- a signum property set to 1,
- a mag array, with 64 bits total, where only the most significant bit set (1000 0000 … 0000).
Firstly, let’s create a BigInteger using the setBit(int n) function:
BigInteger bi1 = BigInteger.ZERO.setBit(63);
String str = bi1.toString(2);
assertEquals(64, bi1.bitLength());
assertEquals(1, bi1.signum());
assertEquals("9223372036854775808", bi1.toString());
assertEquals(BigInteger.ONE, bi1.substract(BigInteger.valueOf(Long.MAX_VALUE)));
assertEquals(64, str.length());
assertTrue(str.matches("^10{63}$")); // 1000 0000 ... 0000
Remember that in the binary representation system, bits are ordered from right to left, starting from 0. While the BigInteger.ZERO has an empty magnitude array, setting the 63rd bit makes it at the same time the most significant – the zeroth element of the 64 length array. The signum is automatically set to one.
On the other hand, the same bit sequence is represented by the Long.MIN_VALUE. Let’s transform this constant into byte[] array and create construct the BigInteger:
byte[] bytes = ByteBuffer.allocate(Long.BYTES).putLong(Long.MIN_VALUE).array();
BigInteger bi2 = new BigInteger(1, bytes);
assertEquals(bi1, bi2);
...
As we see, both values are equal, so the same pack of assertions applies.
Finally, we can inspect the internal int[] mag variable. Currently, Java doesn’t provide API to get this value, but we can do it by evaluation tool in our debugger:
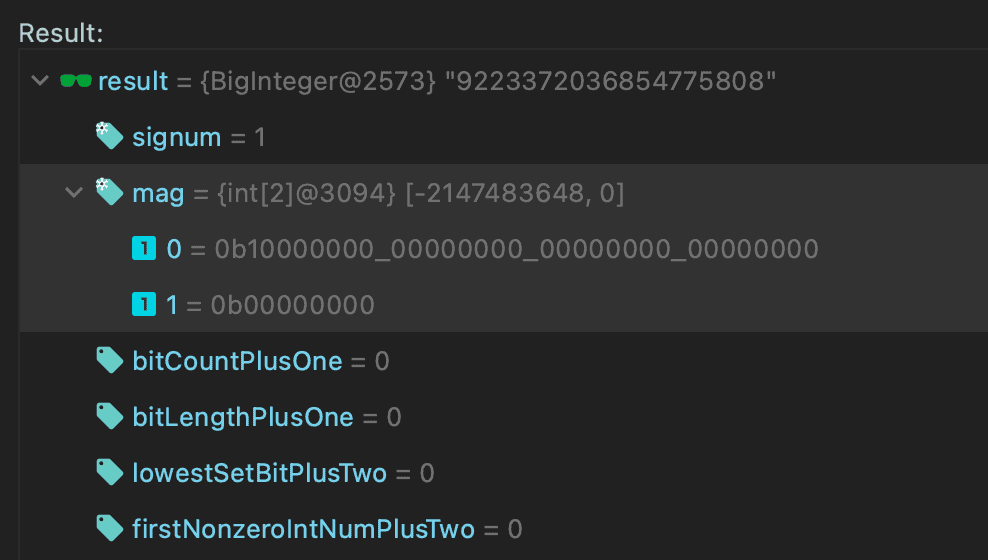
We store our value in the array using two integers, two packs of 32-bits. The zeroth element is equal to Integer.MIN_VALUE and the other is zero.
4. Conclusion
In this quick tutorial, we focused on the implementation details of the BigInteger class. We started by reminding some information about numbers, primitives, and the binary representation rules.
Then we inspected the source code of the BigInteger. We checked signum and mag properties. We also learned how the BigInteger stores the given value, allowing us to provide larger numbers than available primitive data types.
As always, we can find all code snippets and tests over on GitHub.





