What Is the Time Complexity of Tree Traversal?

1. Overview

In Computer Science, linear data structures can be traversed in only one logical way. However, a tree data structure can be traversed in several different ways.

In this tutorial, we’ll discuss various ways to traverse a tree and the time complexity of such an operation.

2. What Is Tree Traversal?

Tree traversal is the process of visiting each node in a tree exactly once. Now from a current node, there might be more than one node we can reach. Therefore, it’s possible to have several different orders in which the nodes are visited. Let’s take an example:

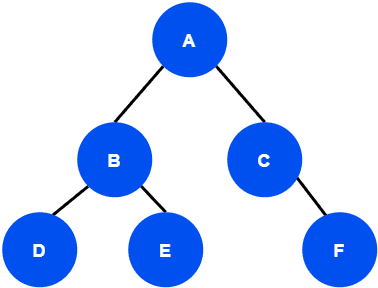
The nodes of this tree can be traversed in many different ways. Some traversal orders are:

• Order 1:
• Order 2:
• Order 3:

Hence depending on the nodes being visited, the traversal is classified into two categories: depth-first traversal and level order or breadth-first traversal.

The depth-first traversal can be further divided into three types of traversal: in-order, pre-order, and post-order traversal.

3. Tree Traversals Techniques

According to in-order traversal, we visit the nodes in the left subtree first, followed by the root node and the nodes in the right subtree. We first search for the left leaf node of the left subtree to start the in-order traversal.

In pre-order traversal, we visit the root node first, then the left subtree, and finally the right subtree.

In the case of post-order traversal, we visit the left subtree, then the right subtree, and finally the root node.

Finally, for level-order or breadth-first traversal, we visit all the nodes in a tree level by level fashion. We start with the root node and goes to the next level to visit the nodes.

4. Example

Now we’re taking an example tree, and let’s find the various traversals of the tree:

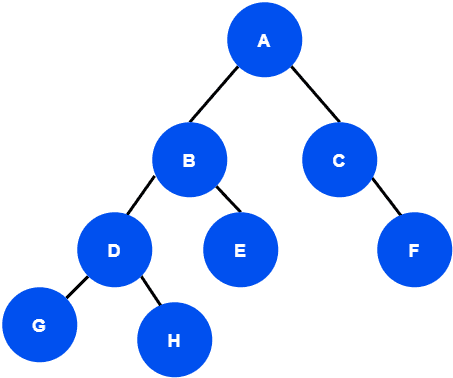
If we apply in-order traversal in this example tree, the in-order traversal of this tree would be 

In the case of pre-order traversal, we visit the root node first. Hence the pre-order traversal of this tree would be: 

In the post-order traversal, we traverse the root node at the end. Therefore the post-order traversal of this tree would be:

The level-order traversal of the example tree would be:

5. Time Complexity of the Tree Traversals

In the general case, all the traversal algorithms visit each node in a tree exactly once. Therefore the time complexity of all the traversal algorithms would be when a tree contains nodes.

In order to verify the overall time complexity, we’re taking a corner case, and we’re going to find the time complexity to visit all the nodes. If a tree has nodes, then the time complexity of the tree can be defined as:

is the number of nodes on the left side of the tree, and denotes a constant time. Now let’s assume that the given tree is a right-skewed tree. In the case of a right-skewed tree, the left of the tree will be empty. So :

If we continue, we’ll get:

denotes traversing an empty tree which takes constant time:

Therefore, we verified that all the tree traversal algorithms take time.

6. Conclusion

In this tutorial, we learned several ways to traverse a tree. We presented algorithms for each traversal and demonstrated with an example. Finally, we analyzed the time complexity of the traversal algorithms.