How to Test if a Number Is a Fibonacci Number | Baeldung on Computer Science

1. Overview

In this tutorial, we’ll discuss the Fibonacci series. We’ll define the Fibonacci series and explore various methods to generate Fibonacci numbers with examples.

Finally, we’ll present the pseudocode to check if a given number is a Fibonacci number or not.

2. Fibonacci Series

The Fibonacci series can be defined as the sequence of numbers: $(0, 1, 1, 2, 3, 5, 8, 13, 21, 34, .....)$ . The Fibonacci series was initially elaborated and used in Indian mathematics by Pingala. However, it was illustrated to the world by Leonardo Pisano Bogollo, later known as Fibonacci.

Additionally, the Fibonacci series follows an interesting property. The property is we can find the next element in the series by adding two elements that appear before it:

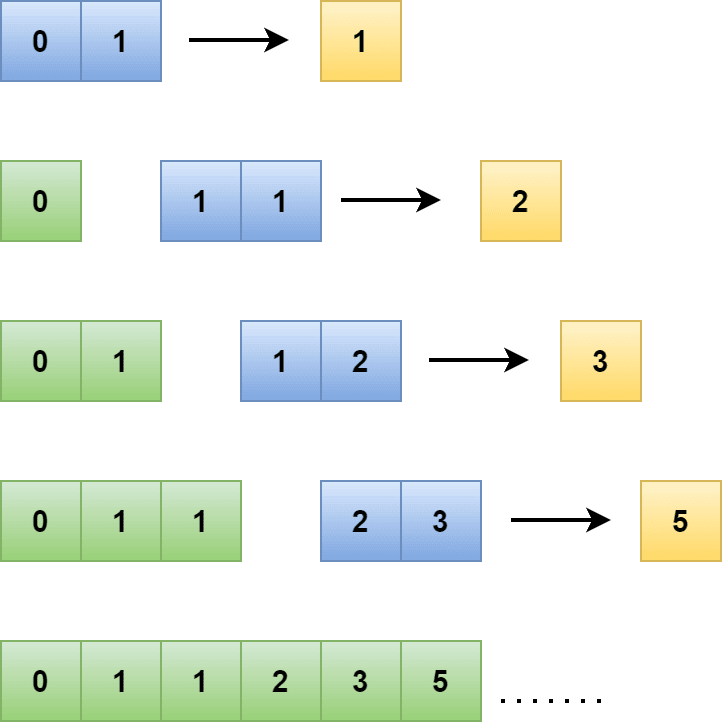
Let’s verify the property. Element 34 can be found by adding two previous elements, 21 and 13 (21 + 13 = 31). Similarly, we can find element 8 by adding two previous elements, 5 and 3. Additionally, we can find the next element of 34 in the series. It’ll be 55 (34 + 21).

Now, let’s derive a generalized equation for generating the Fibonacci series. Initially, it starts with initial data $S_{0}=0$ and $S_{1}=1$ , which are given in advance. Moreover, the series proceeds further by adding two previous adjacent elements. Hence, the element at the position $x$ in the series can be calculated as:

$S_{x}=S_{x-1}+S_{x-2}, x>=2, S_{0}=0, S_{1}=1$

Additionally, the numbers that are part of the Fibonacci series are known as the Fibonacci numbers. Hence, the Fibonacci series helps us to verify if a given number is a Fibonacci number or not.

3. Binet’s Formula

Besides the general property, there’s another way to find the elements in the Fibonacci sequence. We can generate the elements in the Fibonacci series using the golden ratio method. Additionally, it’s popularly known as Binet’s formula. Therefore, the equation to find the $x^{th}$ element in the series is:

$S_{x}=\frac{\varphi^{x}- \psi^{x}}{\varphi - \psi}$

The variable $\varphi$ represents the golden ratio. Additionally, the variable $\psi$ is the conjugate of $\varphi$ . Therefore, we can express $\psi$ in form of $\varphi$ :

$\psi = 1 - \varphi$

Therefore, we can simplify Binet’s formula:

$S_{x}=\frac{\varphi^{x}- (1 - \varphi)^{x}}{2\varphi - 1}$

Moreover, the golden ration $\varphi$ can be expressed as:

$\varphi=\frac{1+\sqrt{5}}{2}\simeq 1.618034, (1 - \varphi) \simeq 0.618034$

Hence, the final equation is:

$S_{x}=\frac{1.618034^{x}-0.618034^{x}}{\sqrt{5}}$

Now, let’s verify this formula. Therefore, we’ll calculate some elements from the Fibonacci series and compare them with the Fibonacci series presented in the previous section. Let’s check for $x =$ 5:

$S_{5}=\frac{1.618034^{5}-0.618034^{5}}{\sqrt{5}}=4.919349\simeq5$

Next, let’s set $x$ to 6:

$S_{6}=\frac{1.618034^{6}-0.618034^{6}}{\sqrt{5}}=8.000000\simeq8$

Finally, we set $x =$ 7:

$S_{7}=\frac{1.618034^{7}-0.618034^{7}}{\sqrt{5}}=12.969194\simeq13$

Hence, as we can see using Binet’s formula, we can generate the elements of the Fibonacci series.

4. Approach for Checking a Fibonacci Number

As of now, we know how to generate the elements in the Fibonacci series. Now let’s discuss how to check whether a given number is a Fibonacci number or not. First, let’s look at the flowchart:

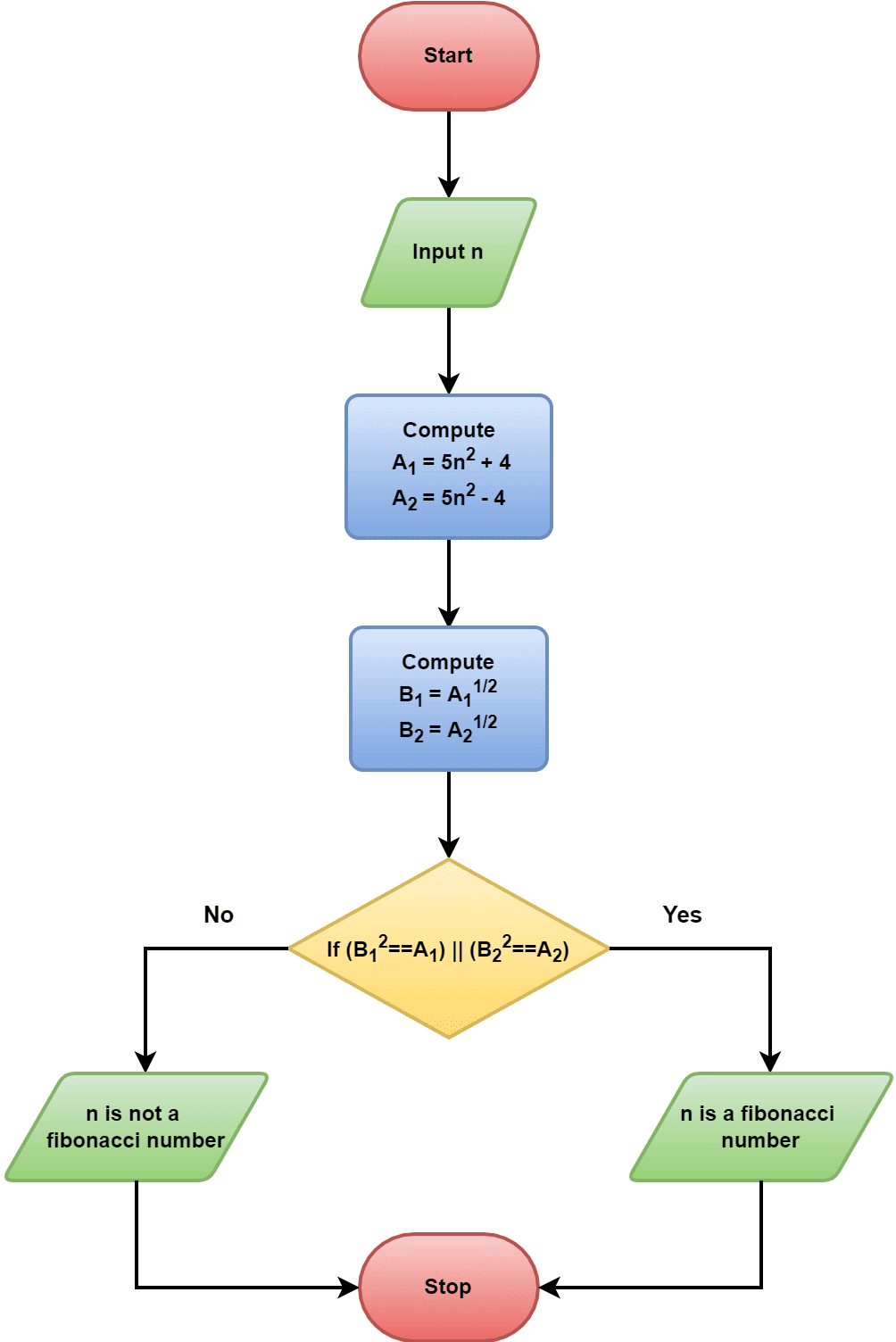
Initially, we input a number $n$ to start the checking process. In the next step, we compute two variables $A_1$ and $A_2$ :

$A_1=5 n^{2}+4, A_2=5 n^{2}-4$

Additionally, we check if any of them is a perfect square or not. In mathematics, a number is a perfect square if we can express it as a product of two equal integers. A number $p$ is a perfect square if $q=\sqrt{p}$ and $\quad q^2 ==p$ .

Therefore, in order to check if $A_1$ or $A_2$ is a perfect square or not, we compute $B_1$ and $B_2$ . Finally, the given number $n$ is a Fibonacci number, if at least one of $A_1$ or $A_2$ is a perfect square.

5. Pseudocode

Now let’s take a look at the pseudocode:

Initially, we take a given number $n$ as an input, and the pseudocode returns whether the number is a Fibonacci or not. Let’s analyze the time complexity of the pseudocode. In this pseudocode, we can only input a single number. Hence, both time and space complexity are ${\mathcal{O}(1)}$ . Moreover, if we want to input an array and the total number of elements in the array is $\mathbf{N}$ , the time complexity would be ${\mathbf{\mathcal{O}(N)}}$ .

6. Validation of Pseudocode

Let’s verify the pseudocode with some examples. Let’s take $n = 5$ as input and run the pseudocode:

$A_1=5(5*5)+4=129, A_2=5(5*5)-4=121, B_1= \sqrt{A_1} = \sqrt{129} =11.36, B_2= \sqrt{A_2} = \sqrt{121} =11$

In this example as we can see $B_2^{2} = A_2$ . Hence, the input number 5 is a Fibonacci number. Let’s take another example. In this case, the given input number is 7. The number 7 isn’t part of the Fibonacci series. Hence, it’s not a Fibonacci number. Let’s run the pseudocode and verify it:

$A_1=5(7*7)+4=249, A_2=5(7*7)-4=241, B_1= \sqrt{A_1}= \sqrt{249} =15.78, B_2= \sqrt{A_2} = \sqrt{241}=15.52$

Here, neither $B_1^{2} = A_1$ nor $B_2^{2} = A_2$ . Both 249 and 241 are not perfect squares. Therefore, the given input $\mathbf{7}$ is not a Fibonacci number.

7. Applications

The Fibonacci series and numbers are used in several applications in the field of computer science and mathematics. In computer science, the Fibonacci numbers are used in lossy compression in audio file format, binary tree representation, Fibonacci heap data structure, Fibonacci cube graph, sorting algorithms, the golden-section search, pseudorandom number generators.

In the mathematics field, many important applications, including optimization method, obtaining the common divisors, number game prediction, dynamic integer generation, use the Fibonacci numbers.

Other fields like high energy physics, quantum mechanics, cryptography utilize the Fibonacci series in various applications.

8. Summary

In this tutorial, we discussed the Fibonacci series and numbers. We talked about two methods to generate the Fibonacci numbers in the Fibonacci series with numerical examples.

Finally, we presented pseudocode for testing a given number is a Fibonacci number or not. We validated the pseudocode with examples.

Full Archive

About Baeldung

Core Concepts

Operating Systems

Artificial Intelligence

Graph Theory

Latex