1. Overview
In this tutorial, we’ll discuss the state space search concept in detail with an example.
Furthermore, we’ll present several applications where we can use this concept.
2. State Space Search
A state space is a mathematical representation of a problem that defines all possible states that the problem can be in. Furthermore, in search algorithms, we use a state space to represent the current state of the problem, the initial state, and the goal state. Additionally, we represent each state in the state space by a set of variables.
State space search is a method used widely in artificial intelligence and computer science to find a solution to a problem by searching through the set of possible states of the problem. Furthermore, a state space search algorithm uses the state space to navigate from the initial state to the goal state. Additionally, it generates and explores possible successors of the current state until we find a solution.
The state space size can greatly affect a search algorithm’s efficiency. Hence, it’s important to choose an appropriate representation and search strategy to efficiently search the state space.
The most famous state space search algorithm is the A* algorithm. Other popular state space search algorithms are breadth-first search (BFS), depth-first search (DFS), hill climbing, simulated annealing, and genetic algorithms.
3. Steps
Now let’s discuss the steps of a typical state space search algorithm:
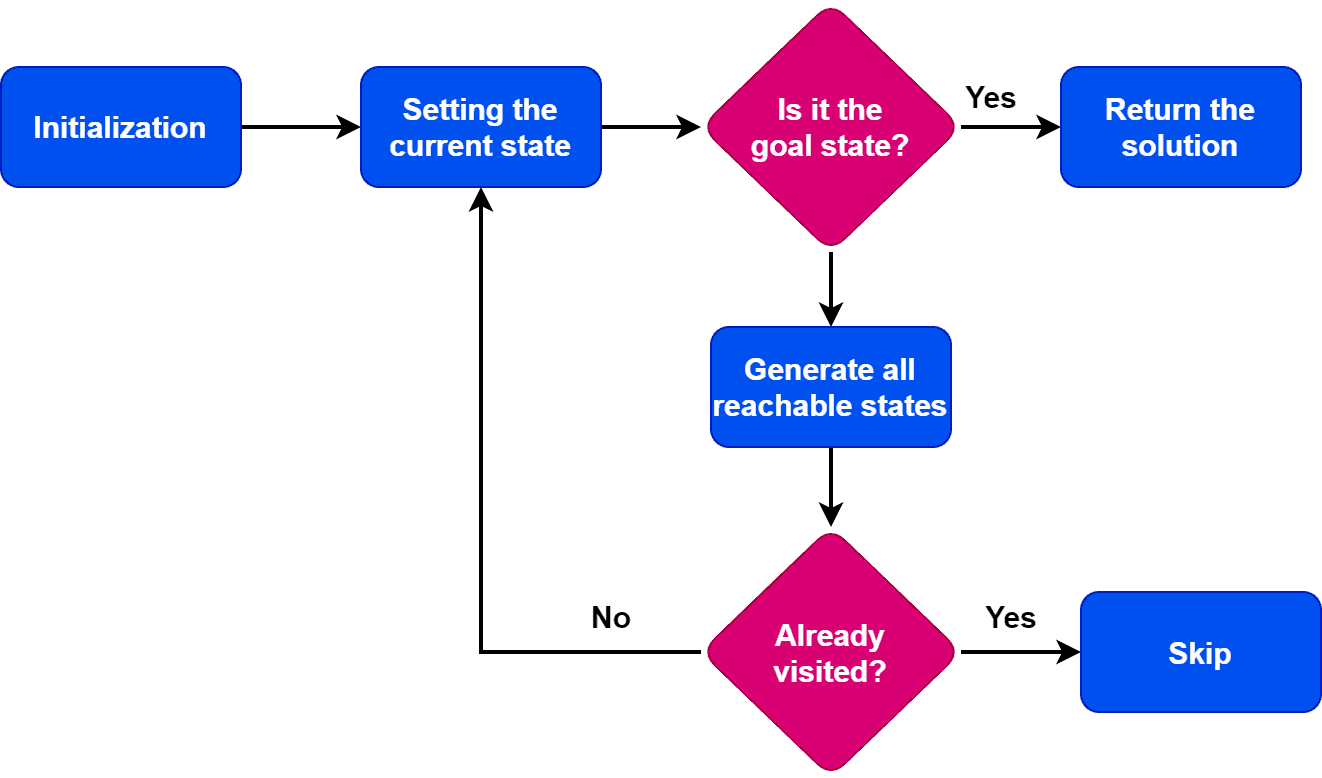
The first step is to initialize the search by setting the initial state as the current state. After the initialization step, we check if the current state is a goal state. Finally, if the current state is a goal state, we terminate the algorithm and return the result.
However, if the current state is not the goal state, we generate the set of possible states that can be reached from the current state. Additionally, these states are known as successor states. Furthermore, for each successor state, we check if it has been previously visited. If the state is already explored, we skip the state. If it has not been visited, we add it to the queue of states to be visited.
Moving forward, we set the next state in the queue as the current state and check if it’s a goal state. If we find the goal state, we return the result. Otherwise, we repeat the previous step until we find the goal state or finish exploring all the states. Furthermore, if all possible states have been explored and we can’t reach the target state, we return with no solution.
The specific implementation details of the algorithm depend on the problem. Additionally, the algorithm’s performance depends on the data structures we use to represent the states and keep track of the search.
4. Example
A common example of a state space search is the 8-puzzle problem. The 8-puzzle is a sliding puzzle that consists of 8 numbered tiles in a 33 grid and one blank space. The goal is to rearrange the tiles from a given initial state to a final goal state by sliding the tiles into the blank space.
In this problem, we represent the state space by the 9 tiles in the puzzle and their positions in the grid. Additionally, we present each state in the state space by a 33 array with values from 1 to 8. Finally, we represent a blank space with an employ tile.
The initial state represents the starting configuration of the tiles. The goal state represents the desired configuration. Furthermore, the search algorithms use the state space to find a sequence of moves that transform the initial state into the goal state.
For example, we can use the breadth-first search to explore all possible states reachable from the initial state. It explores all the states one by one in a sequence. It ensures the solution but can become very slow for large state spaces. Other algorithms, such as A* search, use heuristics to guide the search more efficiently.
We’re taking a practical example of an 8-puzzle problem. Let’s pick current and target states for this example:
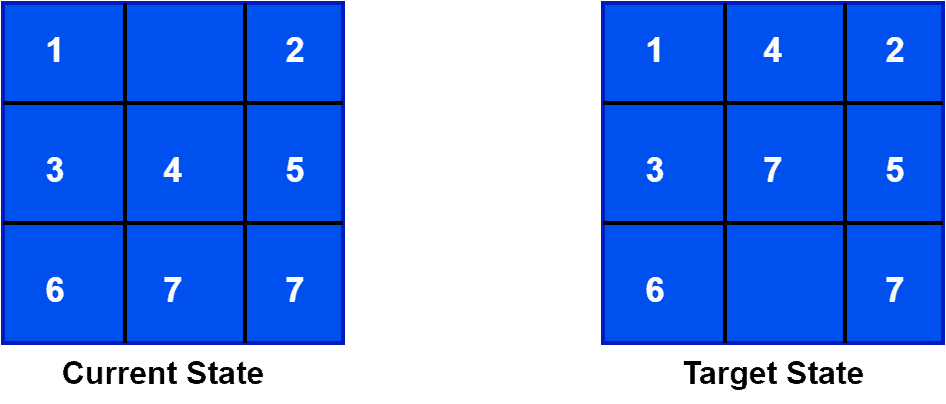
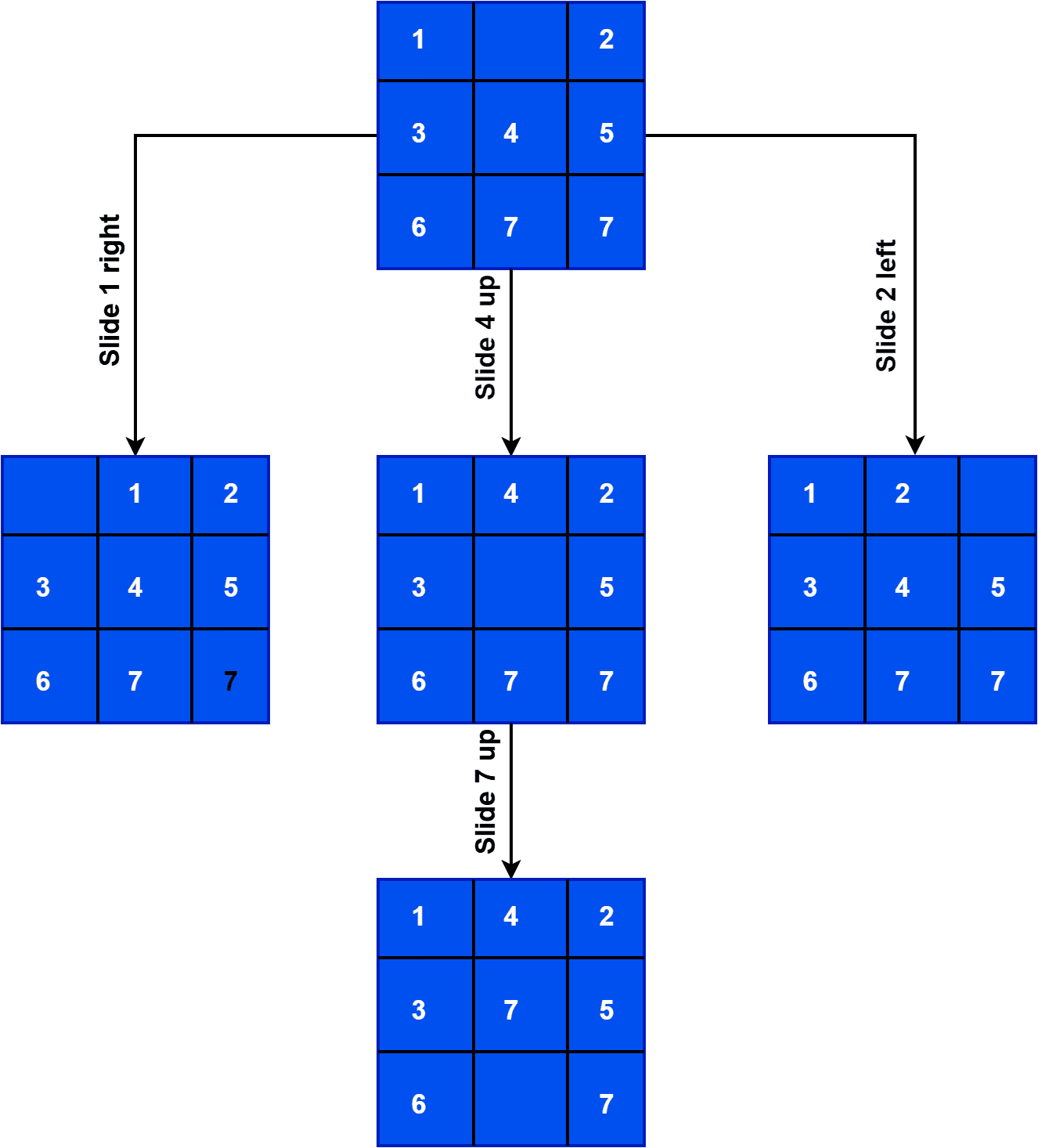
Here, we aim to start from the current state and reach the target state by sliding the numbers through the bank. Furthermore, the approach is to explore all the states we can reach from the current state. For each new state, we check if it’s the target state or not. Let’s take a look at how to reach the target state from the current state:
5. Applications
State space search algorithms have a wide range of applications in various fields, including artificial intelligence, robotics, game playing, computer networks, operations research, bioinformatics, cryptography, and supply chain management.
In artificial intelligence, we can use state space search algorithms to solve problems such as pathfinding, planning, and scheduling. Additionally, we can employ space search algorithms to plan the motion of robots, determining the best sequence of actions to achieve a goal. Furthermore, we also use these algorithms in games to determine the best move for a player, given a particular game state.
In computer networks, we can take advantage of state space search algorithms to optimize routing and resource allocation in computer networks. Additionally, we also use them in operations research to solve optimization problems, such as scheduling and resource allocation. We can also apply these algorithms to find patterns in biological data and predict protein structures in bioinformatics.
In order to find solutions to cryptographic problems, such as breaking codes and finding cryptographic keys, we can employ these algorithms. Furthermore, we can use these algorithms to optimize the flow of goods and resources in logistics and supply chain management.
These are just a few examples of the many applications of state space search algorithms. The ability to efficiently search large state spaces and find solutions to complex problems makes state space search algorithms a powerful tool in a wide range of fields.
6. Conclusion
In this tutorial, we discussed the state space search concept in detail with an example. Furthermore, we explored different fields and applications where it can be extremely useful.