1. Introduction
In this tutorial, we’ll go through the basics of cryptography. To begin with, we’ll cover some basic design principles of cryptography. In the process, it will include the basic elements of cryptography and the categorization of cryptographic ciphers.
Then we’ll understand how cryptography has evolved from the classical state to the modern state.
2. Elements of Cryptography
Cryptography is the study of techniques for secure communications. It involves constructing and analyzing protocols that prevent third parties from reading private messages. A cryptographic system, shortened as cryptosystem, refers to a computer system that employs cryptography.
Further, cryptanalysis refers to the study of cryptosystems with the aim of defeating or weakening them. Sometimes, cryptology is referred to as the combined study of cryptography and cryptanalysis. There are many terms in cryptography that is essential to understand before proceeding further.
2.1. Cipher
Although cryptography is a wider field of study, we often view it as the science of encrypting and decrypting information. Encryption and decryption are widely used to protect data in transit and data at rest. Although it depends on the algorithm in use, there is a common scheme to it:
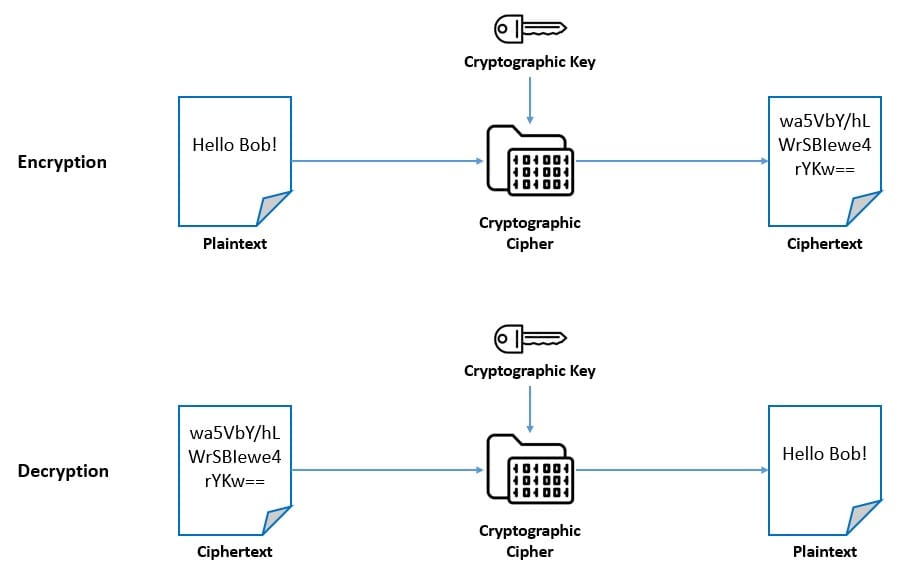
The unencrypted data is called plaintext, and the encrypted data is called ciphertext. A cipher is an algorithm for performing encryption and decryption. The cipher usually depends on a piece of information called the key for performing encryption and decryption.
2.2. Hash Function
The world of cryptography encompasses a few more concepts than just encryption and decryption. One of the important ones is the hash function. Basically, a hash function is a mathematical function that takes inputs of variable lengths to return outputs of a fixed length:
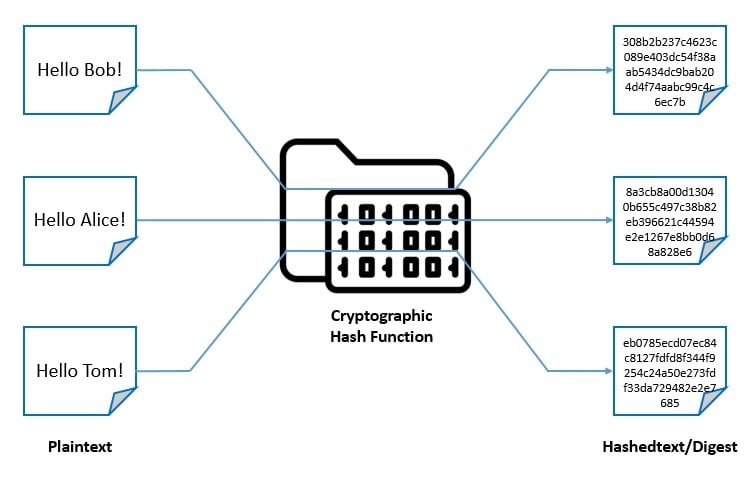
Typically, it should be difficult to guess the input value for a hash function from its output. Moreover, no two input values should map to the same output. It’s widely used for password verification, signature generation and verification, and verifying file and message integrity.
2.3. Pseudorandom Number Generator
A pseudorandom number generator (PRNG) is an algorithm for generating a sequence of numbers whose properties approximate the properties of sequences of random numbers. The PRNG-generated sequence is determined by an initial value called the seed:
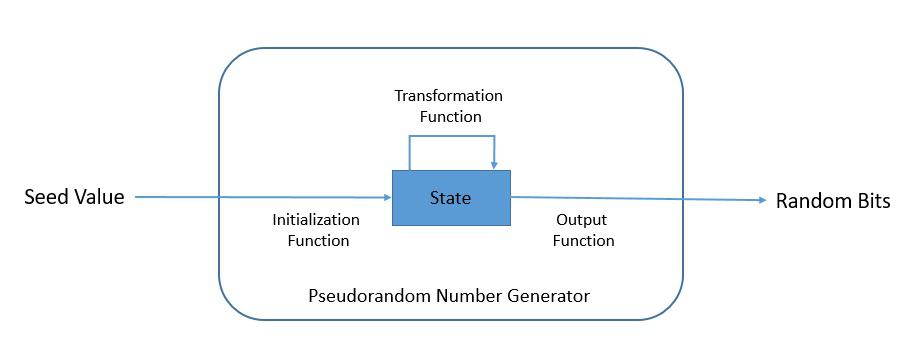
A PRNG typically consists of an initialization function, a state (a sequence of bits of bounded length), a transition function, and an output function. The PRNG-generated sequence should reflect good statistical properties as determined by statistical pattern detection tests.
3. Design Principles of Cryptography
Designing cryptographic algorithms and primitives is a rigorous exercise that needs to pass widespread scrutiny. This is the reason it’s important to have simple design principles. While it’s not in the scope to cover all of them, we’ll discuss the goals for creating a cryptographic system and a few properties for designing a cryptographic algorithm.
3.1. Goals of Cryptography
A cryptographic system helps us to achieve multiple aspects of security in our application. Through the use of one or more cryptographic algorithms, a cryptographic system should be able to fulfill the goals we expect from it. Let’s discuss some of the key goals:
- Confidentiality: The sensitive information should be protected from unauthorized disclosure by concealing the message using an algorithm
- Integrity: It should be possible for the recipient to verify that the message received is the same as the message that was sent
- Non-repudiation: Neither sender nor the recipient of a message should be able to deny later having processed the information
- Authentication: A user or a system should be able to prove their identity to another who does not have personal knowledge of their identity
- Availability: Information should be fully accessible to authorized users and systems at the point in time when it’s needed to make decisions
It’s important to note that not all cryptographic systems achieve all the above goals. More so, some cryptographic systems may have different goals, which may even contradict the above. Nevertheless, it’s important to understand the goals well before designing a cryptographic system.
3.2. Properties of Cryptographic Algorithms
There are some properties that the operations of a secure cipher should exhibit. These are also important in the design of secure hash functions and pseudorandom number generators. Claude Shannon had identified them in his classified report in 1945:
- Confusion: Confusion refers to the property of hiding the relationship between the ciphertext and the key. This makes it difficult to find the key from the ciphertext. It’s possible if every bit of the ciphertext depends on several parts of the key. With this, if a single bit in the key changes, it affects the calculation of most of the bits in the ciphertext.
- Diffusion: Diffusion refers to the property of hiding the statistical relationship between the ciphertext and the plaintext. This helps ensure that any pattern in the plaintext is not apparent in the ciphertext. It’s possible to achieve this if a change in the single bit of plaintext results in a change in about half of the bits in the ciphertext and vice versa.
Basically, these properties help in designing a cryptographic algorithm that can avoid the threat of cryptanalysis. Some ciphers employ just confusion techniques in their constriction, while others use both confusion and diffusion techniques, making them more secure.
3. Categorization of Cryptographic Ciphers
Cryptographic ciphers are often categorized based on their working principles. There are two broad categorizations of modern ciphers. There can be other categorizations based on the internal properties of the algorithm, but we’ll discuss the ones most widely used.
3.1. Categorization Based on Keys
As we’ve seen earlier, a cipher uses a cryptographic key to perform encryption and decryption. The first categorization of ciphers is based on whether it uses the same key for both encryption and decryption or uses different keys for them:
- Symmetric-key Cipher
Symmetric-key cipher is also known as private-key encryption and uses the same cryptographic keys for both the encryption of plaintext and the decryption of ciphertext. The key here represents a shared secret between two or more parties:
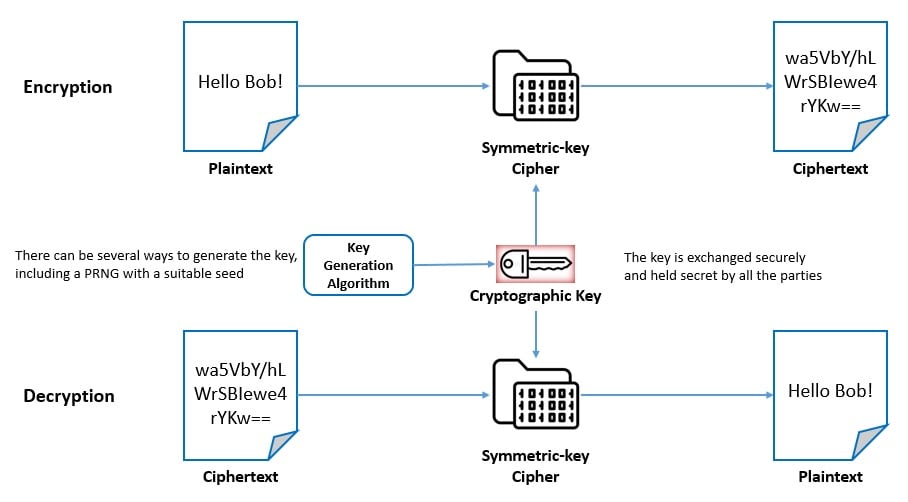
These ciphers have a smaller key size and hence require less storage space and provide faster transmission. But they require all parties to have access to the secret key in advance, which is a major drawback of these algorithms.
- Asymmetric-key Cipher
Asymmetric-key cipher is also known as public-key encryption and uses pairs of related keys for encryption and decryption. Each key pair consists of a public key used for encryption and a private key used for decryption:
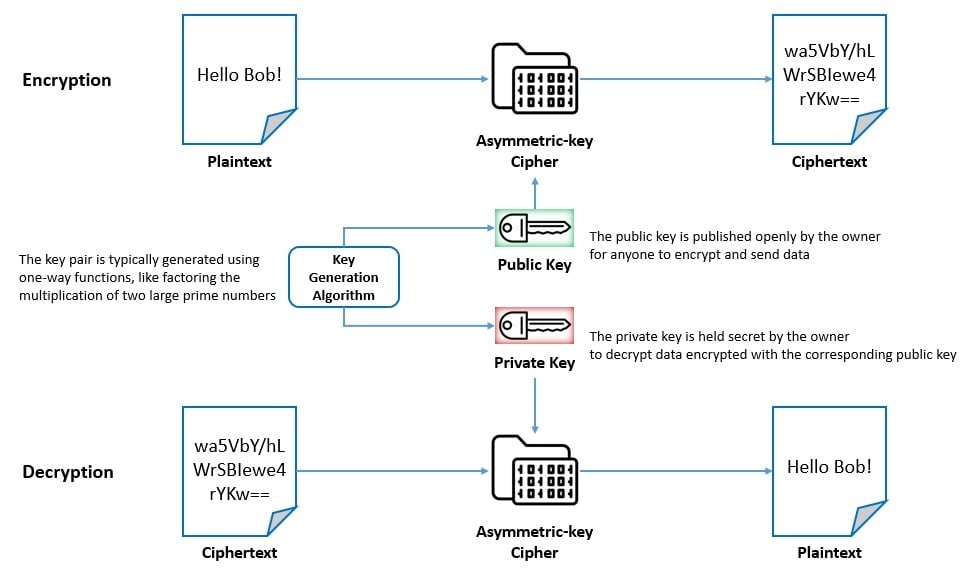
The key pairs are generated with cryptographic algorithms based on one-way functions. Here, the public key is openly distributed but the private key is held secret by the owner of the key pair. However, these algorithms and too slow for many practical purposes like bulk encryption and decryption.
3.2. Categorization Based on Processing
The second way in which we typically categorize ciphers is based on how it works on the plaintext. The board categories are whether they work on streams or blocks of data:
- Stream Cipher
A stream cipher is a symmetric-key cipher that combines the plaintext stream with a pseudorandom cipher digit stream or keystream to generate the ciphertext stream. It encrypts plaintext digits one at a time with the corresponding keystream digit to produce the ciphertext digit:
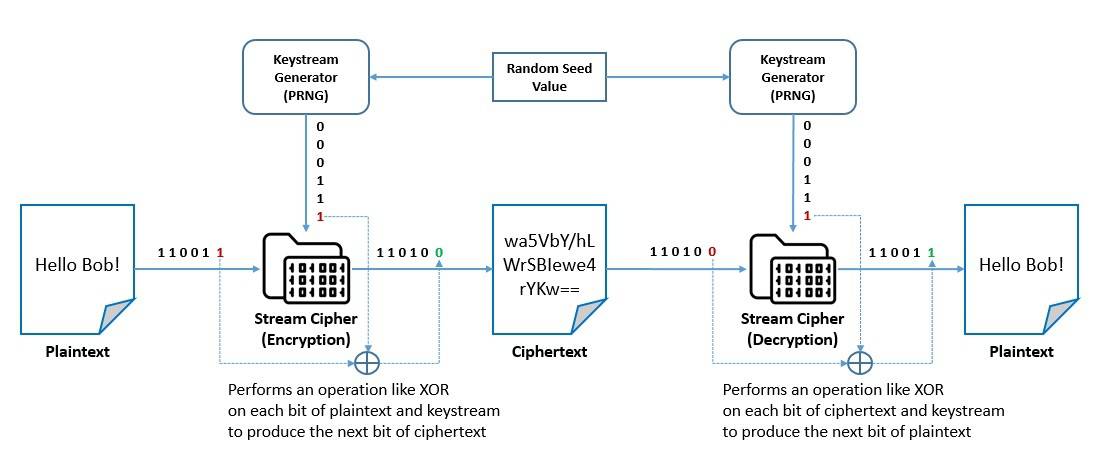
The keystream is typically generated serially from a random seed value using digital shift registers. In a synchronous stream cipher, the key stream is generated independently of the plaintext and ciphertext. In a self-synchronizing stream cipher, the previous ciphertext digits are used to compute the keystream.
Stream ciphers typically execute at higher speeds and have lower hardware complexity. However, through their operations, they only employ confusion. Hence, they are generally susceptible to stream cipher attacks. These threats can be largely mitigated by a better selection of keystreams.
- Block Cipher
A block cipher is a deterministic algorithm that operates on a fixed-length group of bits called blocks. It works with a pair of algorithms, one for encryption and the other for decryption. Both algorithms take an input block of size n-bits and a key of size k-bits to produce an n-bits output block:
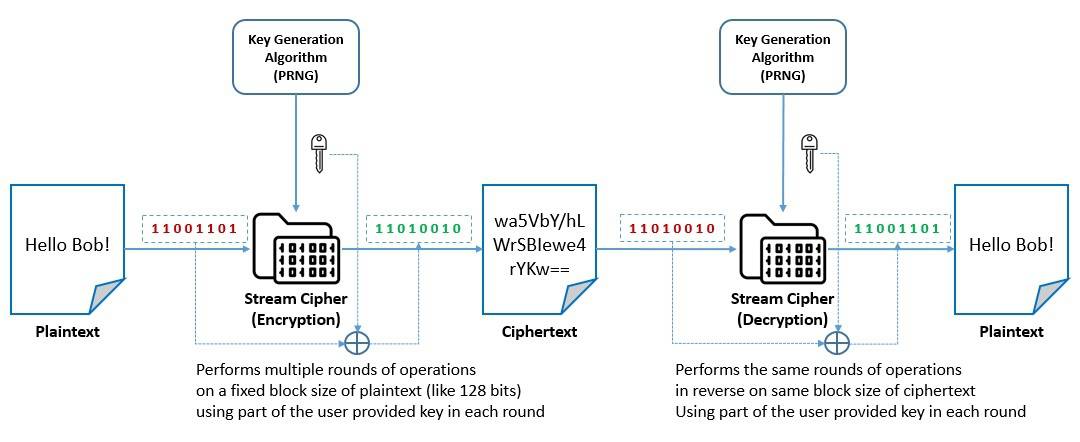
These are basically iterated product ciphers, which carry out encryption in multiple rounds, each of which uses a different subkey derived from the original key. For better security, some of the block ciphers also employ operations like substitutions for confusion and permutations for diffusion.
Block ciphers are only suitable for the secure transformation of data in blocks. For applying block ciphers on variable-length messages, several modes of operation have been developed. These typically provide security like confidentiality, authenticity, or even both in some modes.
4. Beginnings of Cryptography
The earliest known use of cryptography has been traced back to 1900 BCE as carved ciphertext on stone in Egypt. History is scattered with examples of symmetric ciphers like transposition ciphers and substitution ciphers. Substitution ciphers were particularly more popular due to their simplicity.
Many of the earliest substitution ciphers were monoalphabetic. In these ciphers, for a given key, the cipher alphabet for each plain alphabet is fixed. Caesar cipher, also known as the shift cipher, was a popular monoalphabetic substitution cipher credited to the Roman general Julius Caesar:
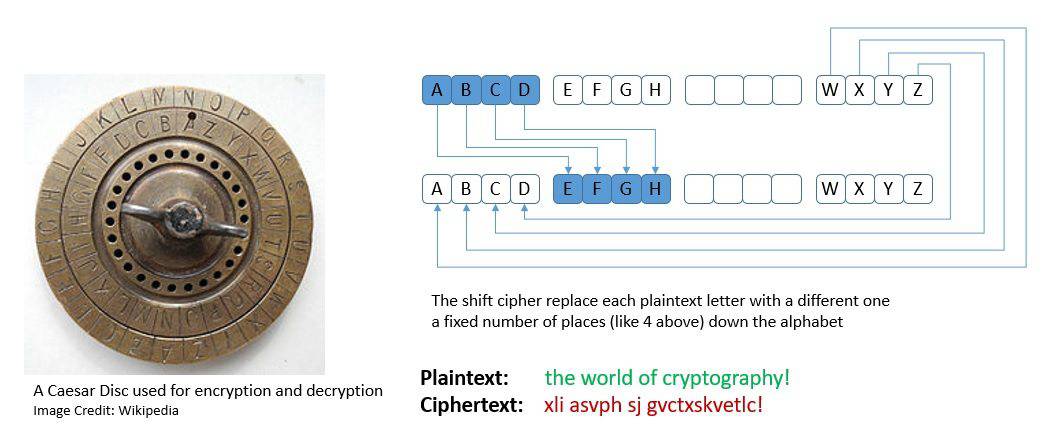
However, monoalphabetic substitution ciphers were quite vulnerable to frequency analysis, a cryptanalysis technique credited to Arab mathematician Al-Kindi. This led to the development of polyalphabetic substitution ciphers that uses multiple alphabets for substitution.
There were also several devices and aids created to assist with ciphers. One of the earliest examples of this is the scytale developed by the Greeks. The era of world wars saw some of the greatest advancements in cryptography.
The Germans developed Enigma, a rotor-based mechanical encryption/decryption device. The machine settings were changed daily based on secret key lists distributed in advance. The usage and the breaking of Enigma mark significant impacts on the course of the war:
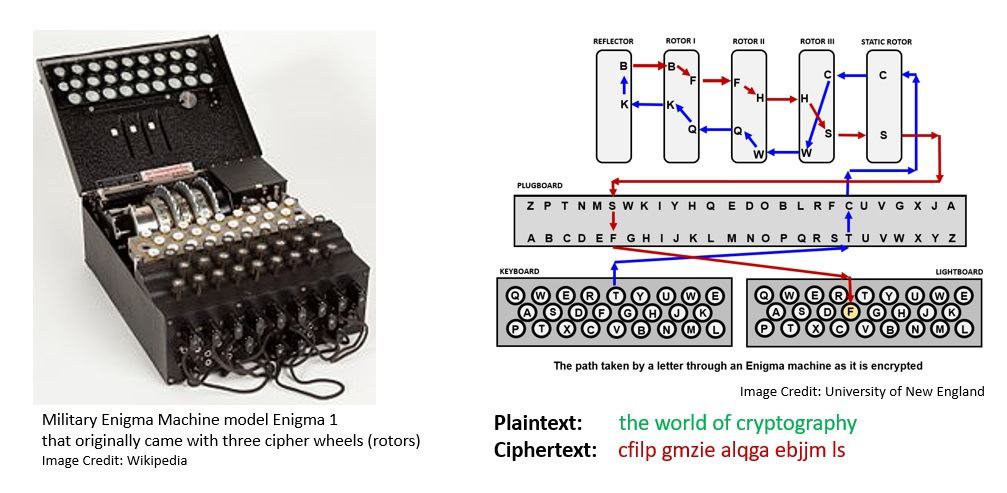
The parallel developments of cryptography and cryptanalysis led to famous principles. Dutch cryptographer Auguste Kerckhoffs stated in the 19th century that “a cryptosystem should be secure, even if everything about the system, except the key, is public knowledge“.
Later American mathematician Claude Shannon rephrased this as the fact that “the enemy knows the system“. Claude Shannon also proved in 1949 that a properly implemented One-time Pad (OTP) system is the only encryption technique that cannot be cracked.
Frank Miller first described OTP in 1882. It’s basically a stream cipher that requires a single-use pre-shared key that is not smaller than the message. Later Gilbert Vernam also co-invented an automated OTP cipher in 1917.
5. Development of Modern Cryptography
Even though it may be impractical to set a timeline, we can refer to the post wars era as the most influential in modern cryptography. This was when it found commercial usage apart from military applications. While stream and block cryptography continued to evolve during this period, it also saw the emergence of asymmetric cryptography.
5.1. Development of Stream Ciphers
Most of the stream ciphers took inspiration from the OTP and tried to approximate it in a more practical setup. They use a much smaller and more convenient key, such as 128 bits. Based on this key, they generate a pseudorandom keystream to combine with the plaintext.
The earliest developments in stream cipher can be attributed to Gilbert Vernam. In fact, a Vernam cipher came to refer to any stream cipher in which the plaintext is combined with a pseudorandom stream of data using the Boolean “exclusive or” function.
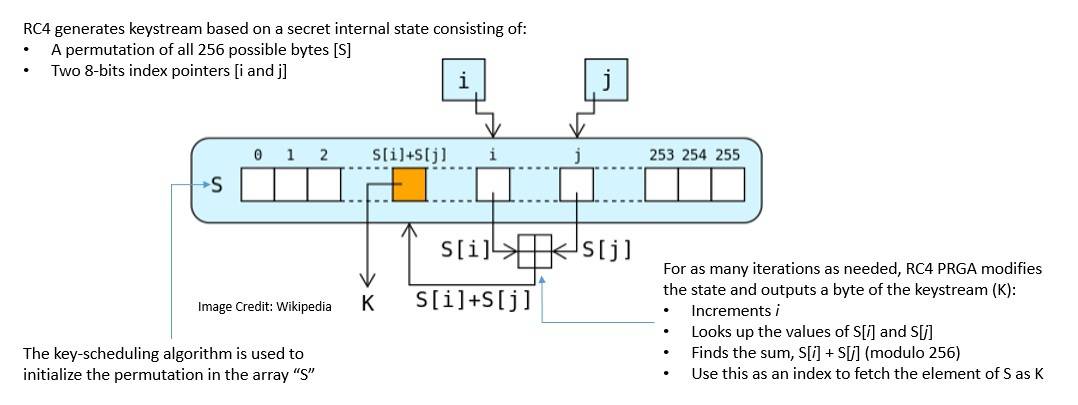
One of the most popular Vernam ciphers is RC4 which was designed by Ron Rivest in 1987. It generates the pseudorandom keystream based on a secret internal state:
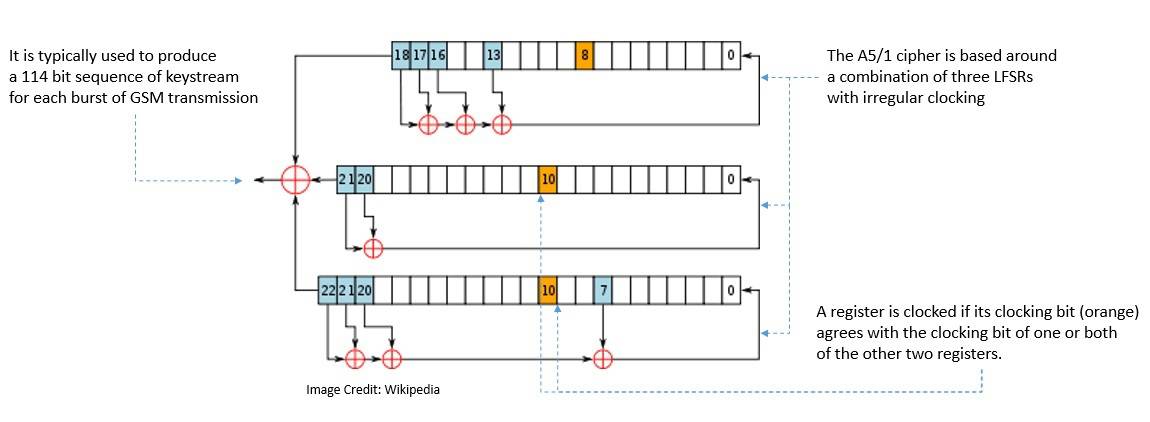
Binary stream ciphers were also constructed using linear-feedback shift registers (LFSRs) as they are easy to implement in the hardware. For instance, the A5/1 cipher was developed in 1987:
However, these historical stream ciphers have been reported with several vulnerabilities. The more modern versions of stream ciphers include the Salsa20 cipher, designed in 2005, and its variant, the ChaCha cipher, published in 2008, both developed by Daniel J. Bernstein.
5.2. Development of Symmetric-key Block Ciphers
One of the earliest ciphers of the modern era was Lucifer, created by Horst Feistel at IBM in 1971. It was accepted in 1976 with some modifications as the Data Encryption Standard (DES) by the National Bureau of Standards (NBS).
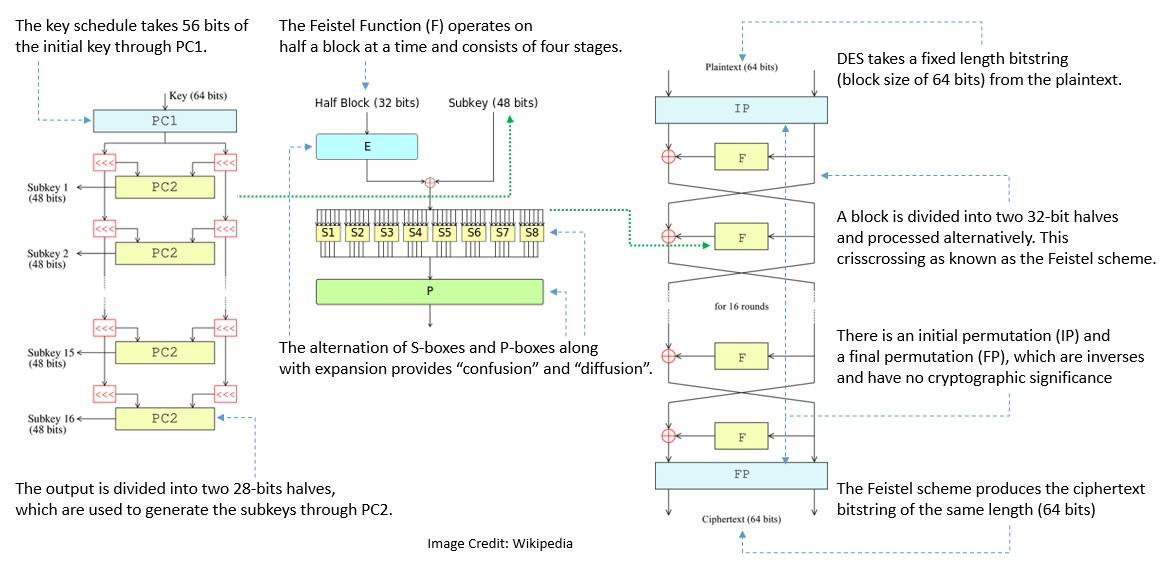
DES is a symmetric-key block cipher based on the balanced Feistel network. Here, both encryption and decryption consist of running 16 identical stages of processing, called rounds:
After publication by NBS, DES was soon internationally accepted and also scrutinized. However, due to its internal weaknesses, DES was mostly broken in the 1990s. It led to variants like Triple DES, but those could not fill the void.
In 1997, the National Institute of Standards and Technology (NIST, a successor to NBS) put out a request for a new cipher. In 2000, it accepted a variation of Rijndael as the Advanced Encryption Standard (AES). Rijndael was developed by Joan Daemen and Vincent Rijmen.
Like DES, AES is also a symmetric-key block cipher. But it’s based on a design principle known as the substitution-permutation network. It consists of 10, 12, or 14 rounds based on key size:
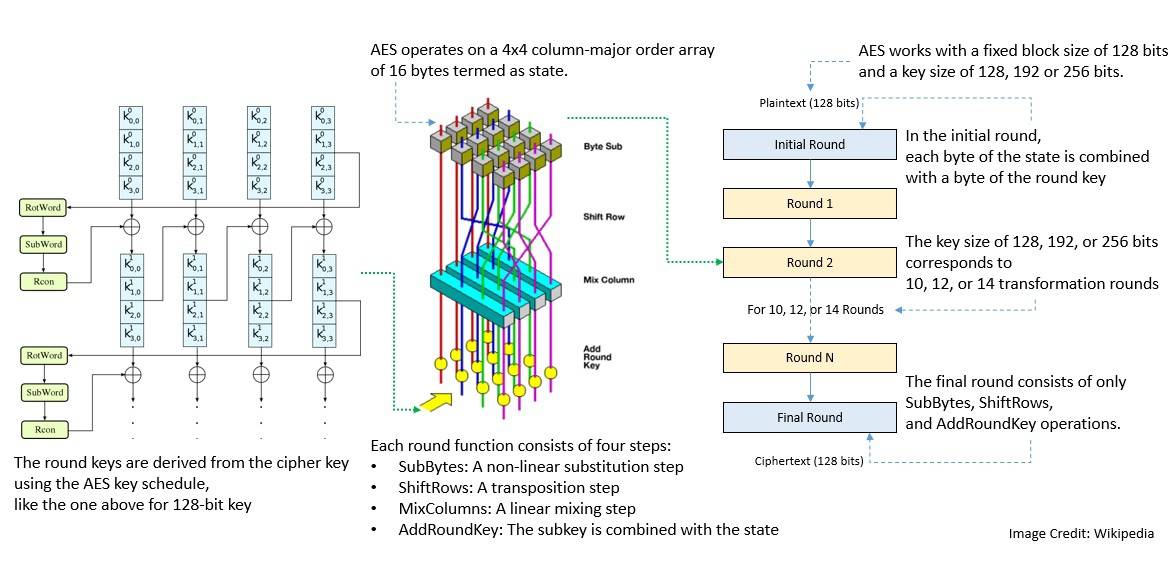
There have been other symmetric ciphers proposed over time. For instance, Bruce Schneier, along with others, came up with the Blowfish cipher in 1993 and the Twofish cipher in 1998. These are based on the Feistel network and feature key-dependent S-boxes and a relatively complex key schedule.
5.3. Development of Asymmetric-key Block Ciphers
As we’ve seen earlier, symmetric-key algorithms like DES and AES have the problem of secure key distribution. To address this challenge Whitfield Diffie and Martin Hellman came up with the idea of asymmetric cryptography in 1976.
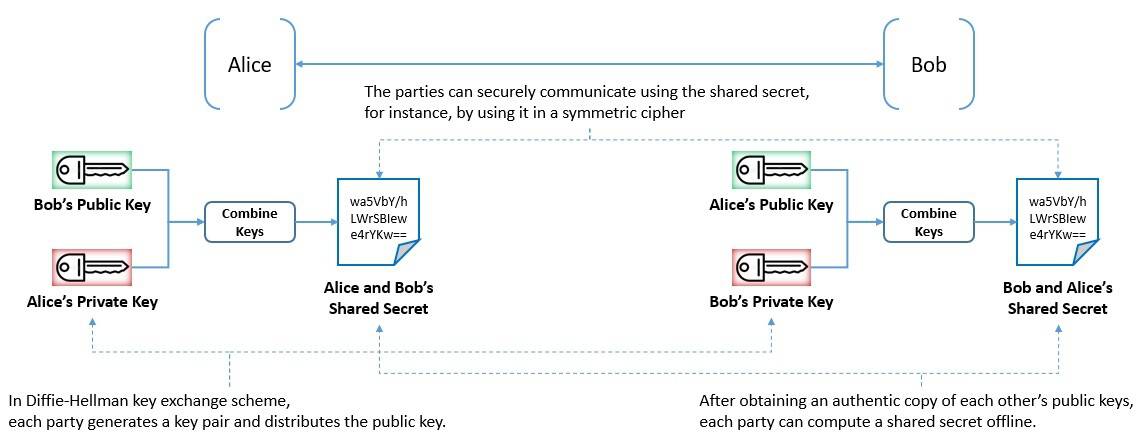
It led to the development of public-key cryptosystems, which were cryptographic systems using pairs of related keys. The earliest such system was the Diffie-Hellman key exchange, conceived by Ralph Merkle:
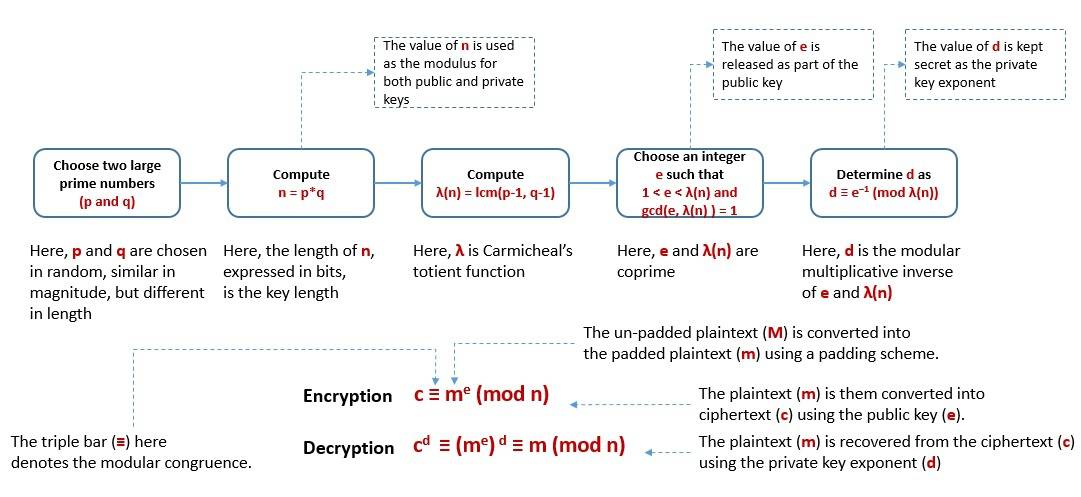
This was soon followed by Rivest-Shamir-Adleman (RSA), developed by Ron Rivest, Adi Shamir, and Leonard Adleman in 1977. RSA relies on the practical difficulty of factoring the product of two large prime numbers:
Another significant public-key cryptosystem is Elliptic Curve Cryptography (ECC), proposed independently by Neal Koblitz and Victor S. Miller in 1985. It’s based on the algebraic structure of elliptic curves over finite fields.
As asymmetric-key algorithms are computationally intensive, they are mostly used to encrypt and exchange keys for symmetric algorithms. They are also widely used to implement digital signatures. A number of internet standards, like Transport Layer Security (TLS), also use them.
5.4. Development of Block Cipher Mode of Operation
As we’ve seen, the practical application of block ciphers requires a mode of operation. Along with the development of block ciphers, their mode of operation also saw significant changes. Most of these developments were coupled with the development of DES and AES standards.
One of the earliest and weakest encryption modes was the Electronic Codebook (ECB) mode. It was the original mode for DES in 1977. Subsequently, other modes were added to DES, like Cipher Block Chaining (CBC) mode, Cipher Feedback (CFB) mode, and Output Feedback (OFB) mode.
Out of these, CBS remains the most commonly used mode of operation. However, it suffers from drawbacks like sequential encryption and the fact that the messages must be padded:
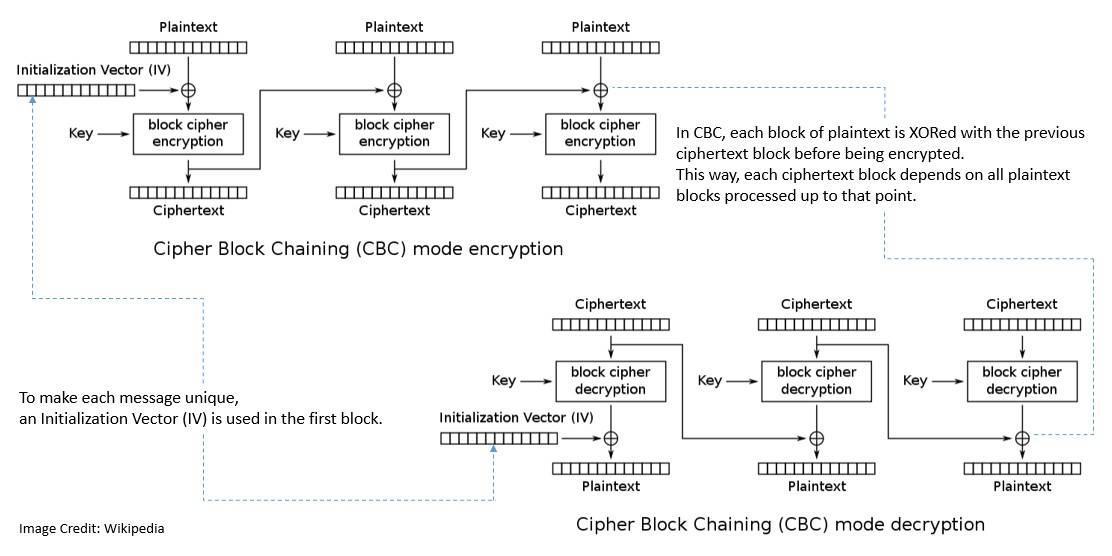
When NIST published AES in 2001, it revised the list of modes, including the Counter (CTR) mode. Later in 2010, Ciphertext Stealing (XTS) mode was also included in the list. However, all these modes of operation only provide confidentiality and do not protect against modification or tampering.
Hence, several encryption modes were developed that combined confidentiality and data integrity. These are known as Authenticated Encryption (AE). Some of the examples are Galois/Counter (GCM), Counter with CBC-MAC (CCM), and AES-GCM with Synthetic Initialization Vector (AES-GCM-SIV).
Many of the modes of operation, including CTR, also use a block of bits called the initialization vector to randomize the encryption. Further, since block cipher works on units of fixed size, some modes like ECB and CBC add padding in the final block for messages coming in varying lengths.
5.5. Development of Hash Function
Besides cryptographic value, hash functions have several non-cryptographic uses, like cyclic redundancy checks and checksums. The first design of cryptographic hash functions dates back to the late 1970s, and more designs kept appearing in the following decades.
One of the most widely used hash functions is Message Digest 5 (MD5), designed by Ronald Rivest in 1991. It succeeded an earlier hash function called MD4. MD5 produces hash values of 128-bits:
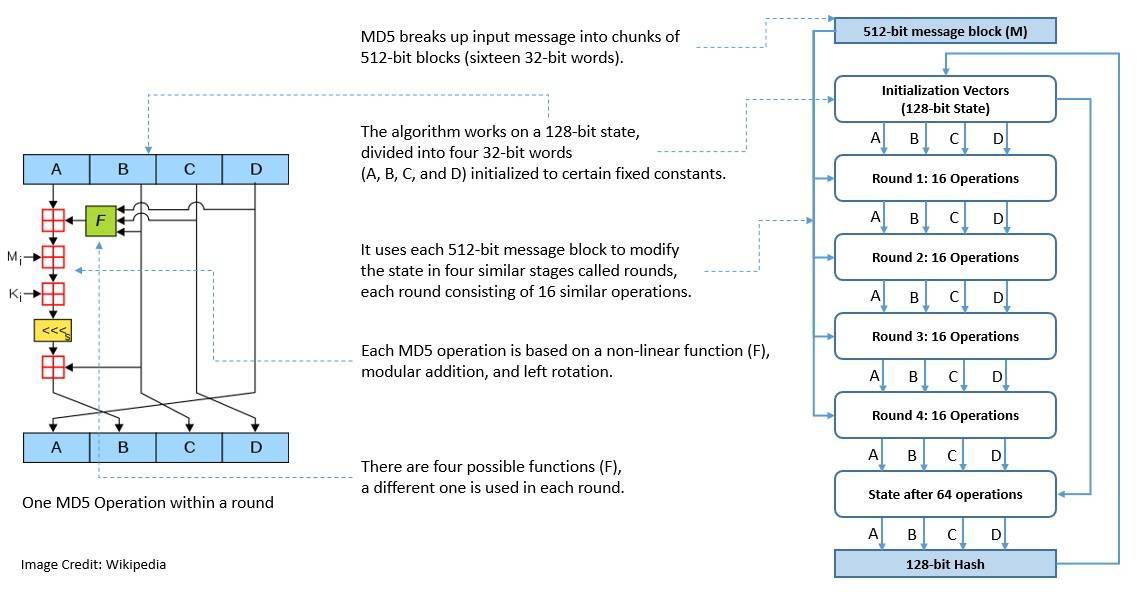
As of 2008, MD5 has been deemed to be cryptographically broken. Although not of cryptographic value, it continues to be widely used as a checksum to verify data integrity.
As part of standardization, NIST has been publishing a family of cryptographic hash functions called the Secure Hash Algorithms (SHA). It began in 1993 with the publication of SHA-0. The latest in this series was chosen in 2012 and is called SHA-3. SHA-3 is a subset of a broader family called Keccak.
5.6. Development of Pseudorandom Number Generator
One of the earliest PRNGs was developed by John von Neumann around 1946. His idea was quite simple but had the problem of short, repeated cycles. Later in 1949, D. H. Lehmer came up with the Linear Congruential Generator (LCG), which addressed this issue to some extent.
For a number of years, several PRNGs continued to be based on the LCG. However, the quality of LCG was known to be inadequate. A major breakthrough in the construction of pseudorandom generators came with the introduction of the linear-feedback shift register (LFSR):
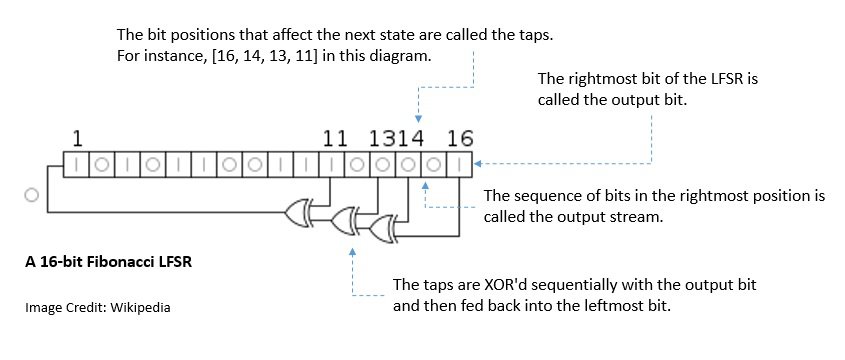
The first such PRNG was the Mersenne Twister, developed by Makoto Matsumoto and Takuji Nishimura in 1997. It chooses its period length to be a Mersenne prime, a prime number that is one than a power of two. It avoided several problems that were there in earlier PRNGs.
Cryptographically Secure PRNGs (CSPRNG) are basically a subset of PRNGs that are suitable for use in cryptography. NIST maintains the list of standard CSPRNGs for use by cryptographic applications. One of the popular names includes Dual_EC_DRBG, which uses methods in elliptic curve cryptography.
6. Applications of Cryptography
Cryptography has been in use for a long time now, and its applications have grown in proportion with the development of computing. Since the early military applications, it has become almost ubiquitous in applications we interact with. It’s almost impossible to cover all the practical uses of cryptography. However, we’ll cover the most popular ones here.
6.1. Digital Signature
A digital signature is a mathematical scheme for verifying the authenticity of digital messages or documents. It employs a hash function and an asymmetric cipher. Further, it consists of a signing algorithm and a signature-verifying algorithm:
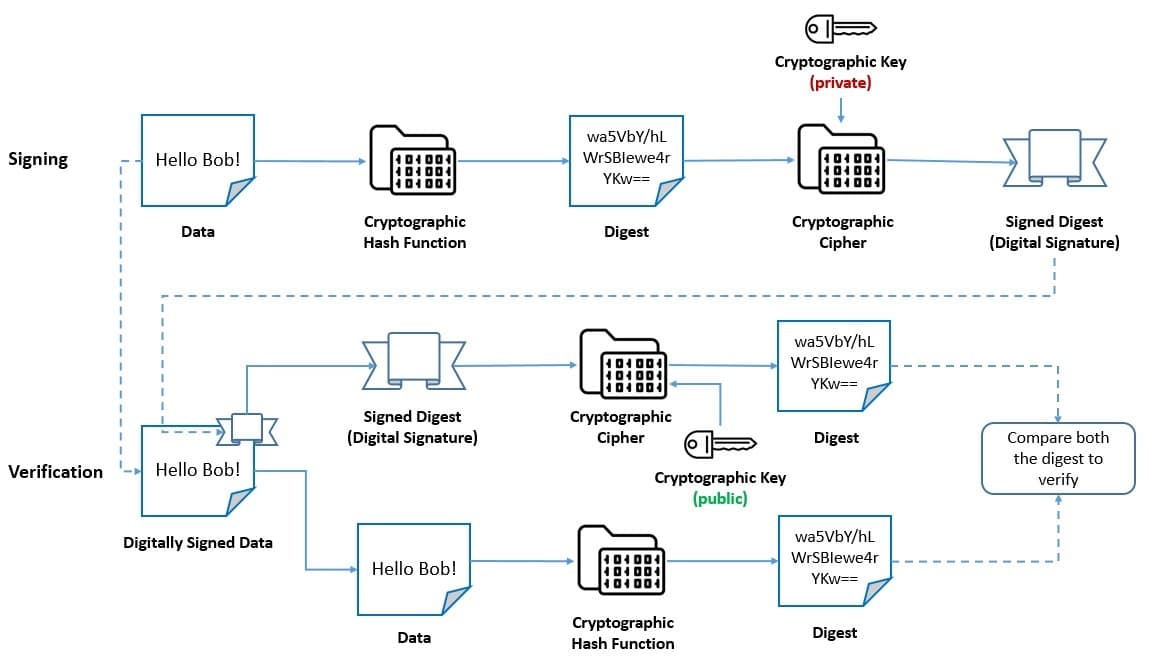
The recipient of a message can verify the authenticity of a signature generated from a fixed message and fixed private key using the corresponding public key. Moreover, it’s computationally infeasible to generate a valid signature for a party without knowing their private key.
Digital Signature Algorithm (DSA) was adopted by the NIST in 1991 as part of their Digital Signature Standard (DSS). DSA is a public-key cryptosystem developed for digital signatures. However, it’s recommended to be superseded by a newer algorithm like Edwards-curve DSA (EdDSA).
6.2. Digital Certificate
A digital certificate is an electronic document used to prove the validity of a public key. Along with other information, a certificate contains the public key, the identity of its owner (subject), and the digital signature of an entity that has verified the certificate’s contents (issuer):
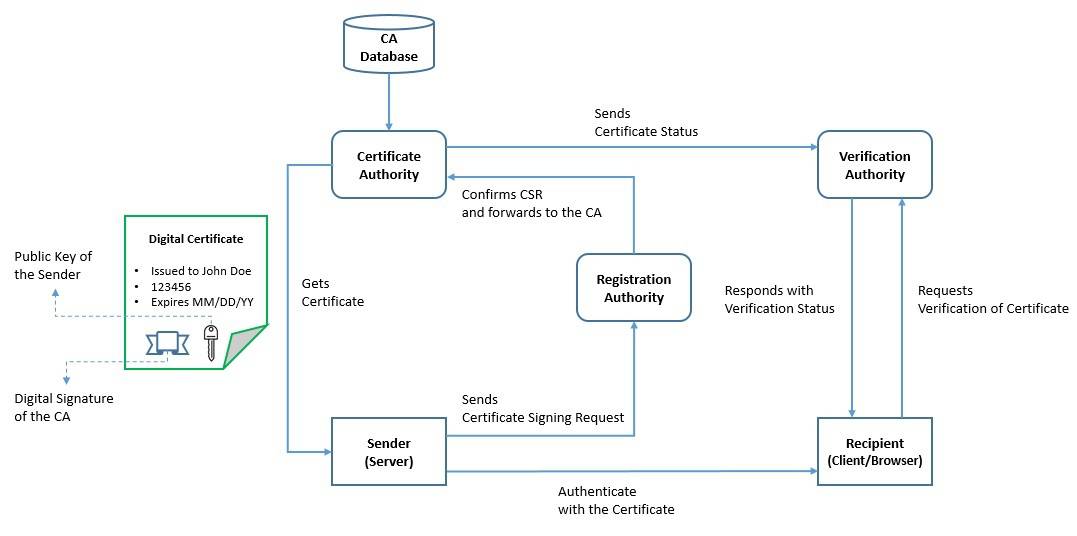
To manage the lifecycle of digital certificates, an elaborate scheme has been created called the Public Key Infrastructure (PKI). It includes roles like Registration Authority (RA) to verify certificate requests, Certificate Authority (CA) to issue certificates, and Verification Authority (VA) to verify certificates.
The most common format for public-key certificates is defined by X.509, a standard defined by International Telecommunication Union (ITU). However, there are more specific formats defined under it, for example, the Public-key Infrastructure (X.509) (PKIX).
6.3. Secure Network Communication
A lot of modern applications require communication over the network, for instance, email and instant messaging. It requires a cryptographic protocol to provide security, confidentiality, integrity, and authenticity. One such protocol is the Transport Layer Security (TLS):
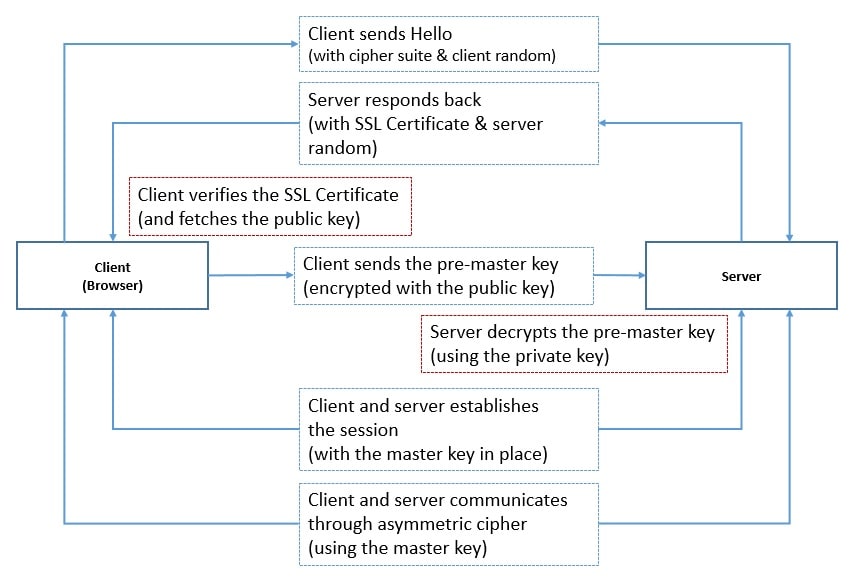
Here, one of the parties negotiates a stateful connection by using the handshaking procedure. TLS handshake uses an asymmetric cipher to agree on various parameters, including a session-specific shared key. This key is used in further communication using a symmetric cipher.
TLS is an Internet Engineering Task Force (IETF) standard, first proposed in 1999. It builds on the earlier protocol called the Secure Sockets Layer (SSL). TLS runs in the application layer of the OSI model and makes use of cryptography primitives like certificates between communicating parties.
7. Conclusion
Cryptography is a vast field of study that has existed for centuries. It has evolved through times of desperation and innovation. While we’ve just scratched the surface of cryptography, much is to be learned. It’s important to note that the security that any cryptographic algorithm provides is only relative and temporal.
Hence, we’ll continue to see innovations in this field in the years to come.