1. Introduction
Graphs are data structures with multiple and flexible uses. In practice, they can define from people’s relationships to road routes, being employable in several scenarios.
Several data structures enable us to create graphs, such as adjacency matrix or edges lists. Also, we can identify different properties defining a graph. Examples of such properties are edge weighing and graph density.
Furthermore, we have some particular classifications and differentiation of graphs according to the connections between nodes. In this case, we take into account how the edges relate with the nodes, forming specific sequences.
Thus, in this tutorial, we’ll in-depth explore the sequences related to the connections between graphs’ nodes. First, we’ll have a brief review of the basic concepts of graphs. So, we’ll study the theory of a path, circuit, and cycle. We’ll also have a concise explanation about walks and trails. Finally, we’ll compile the concepts in a systematic summary.
2. Graph Basics
Graphs are data structures formed by nodes (also called vertices) and edges. Nodes are fundamental elements of a graph. Actually, nodes are abstractions of particular objects in a graph.
In practice, we identify a data structure as a graph if it contains at least one node. However, graphs with no nodes and, by consequence, no vertices are often called null graphs.
Edges, in turn, are the connections between two nodes of a graph. Edges are optional in a graph. It means that we can concretely identify a graph without edges with no problem. In particular, we call graphs with nodes and no edges of trivial graphs.
So, the traditional notation of a graph consists of a two sets: V (vertices) and E (edges). In this way, we can denote a generic graph as G = (V, E), with and
.
The following image depicts a simple and generic graph:
3. Path
In practical terms, a path is a sequence of non-repeated nodes connected through edges present in a graph. We can understand a path as a graph where the first and the last nodes have a degree one, and the other nodes have a degree two.
If the graph contains directed edges, a path is often called dipath. Thus, besides the previously cited properties, a dipath must have all the edges in the same direction.
The following image shows particular examples of paths and dipaths:
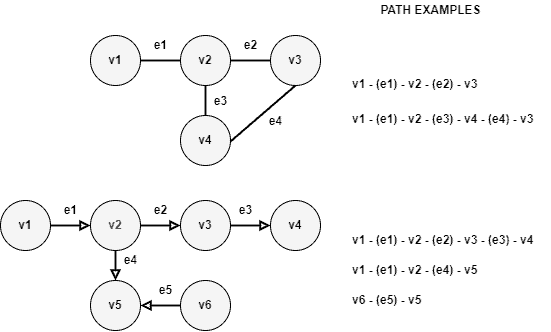
By analyzing the available paths of a graph, we can draw some conclusions:
- A graph is, at least, weakly connected when there is an undirected path (disregarding the directions in a directed graph) between any two nodes
- If a directed graph provides the opposite oriented path for each available path, the graph is strongly connected
- If there are one or more paths between two nodes in a graph, the distance between these nodes is the length of the shortest path (otherwise, the distance is infinity)
4. Circuit
A circuit is a sequence of adjacent nodes starting and ending at the same node. Circuits never repeat edges. However, they allow repetitions of nodes in the sequence.
There are two particular categories of circuits with specific characteristics:
- Eulerian: this circuit consists of a closed path that visits every edge of a graph exactly once
- Hamiltonian: this circuit is a closed path that visits every node of a graph exactly once.
The following image exemplifies eulerian and hamiltonian graphs and circuits:
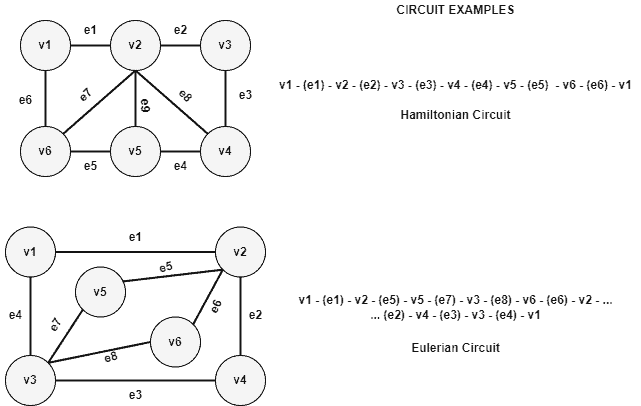
We can note that, in the previously presented image, the first graph (with the hamiltonian circuit) is a hamiltonian and non-eulerian graph. So, there is no way to create an eulerian circuit with it.
Similarly, the second graph (with the eulerian circuit) consists of an eulerian and non-hamiltonian graph. Thus, there is no possible hamiltonian circuit on it.
5. Cycle
A cycle consists of a sequence of adjacent and distinct nodes in a graph. The only exception is that the first and last nodes of the cycle sequence must be the same node.
In this way, we can conclude that every cycle is a circuit, but the contrary is not true. Furthermore, another inferring is that every Hamiltonian circuit is also a cycle.
So, we call a graph with cycles of cyclic graphs. Oppositely, we call a graph without cycles of acyclic graphs. Finally, if a connected graph does not have cycles, we call it a tree.
The image next presents an example of a cyclic graph, acyclic graph, and tree:
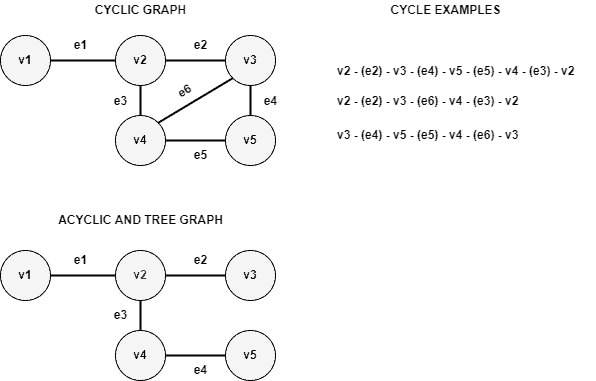
Cycle detection is a particular research field in graph theory. There are algorithms to detect cycles for both undirected and directed graphs. There are scenarios where cycles are especially undesired. An example is the use-wait graphs of concurrent systems. In such a case, cycles mean that exists a deadlock problem.
6. Other Sequences: Walks and Trails
Besides the already seen sequences, exist other two that actually are the simplest ones: walks and trails. Thus, let’s briefly see them in this section.
Walks are any sequence of nodes and edges in a graph. In this case, both nodes and edges can repeat in the sequence.
We can categorize a walk as open or closed. Open walks have different starting and ending nodes. Closed walks, in turn, have the same starting and ending nodes. So, circuits and cycles are closed walks, but not every closed walk is a circuit or cycle.
Trails are open walks with no repeated edges in the sequence. However, we can repeat as many nodes as necessary.
The image below shows some examples of walks and trails:
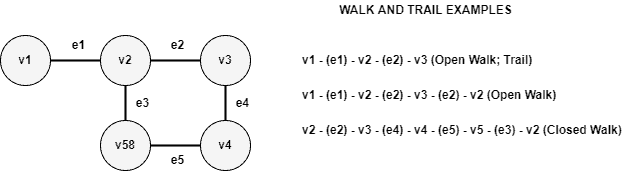
7. Systematic Summary
In the previous sections, we investigated possible nodes and edges sequences formed through the connections in a graph. These sequences are called walks, trails, paths, circuits, and cycles.
The main differences of these sequences regard the possibility of having repeated nodes and edges in them. Furthermore, we define another relevant characteristic on analyzing if a given sequence is open (the first and last nodes are the same) or closed (the first and last nodes are different).
In this way, the following table compares the different sequences of graphs nodes and edges:
It is relevant to highlight that when a sequence can not repeat nodes but is a closed sequence, the only exception is the first and the last node, which must be the same.
8. Conclusion
In this tutorial, we learned about sequences of graphs nodes. First, we briefly reviewed basic concepts about graphs. Thus, we studied the concepts of paths, circuits, and cycles. Next, we investigated walks and trails. Finally, we had a systematic summary approaching all the presented sequences.
We can conclude that analyzing the possible sequences available in a graph enables us to determine several events according to the scenario the graph represents. A usual application of this analysis is searching for deadlocks by detecting cycles in use-wait graphs. Another example consists of finding sequences that indicate better routes to visit particular nodes (the traveling salesman problem).