1. Introduction
In this tutorial, we’ll look at how to create a maze algorithmically.
Since there are many different types of mazes and ways to create them, we’ll only look at perfect mazes in the shape of a square.
2. Types of Mazes
Mazes come in many different types and shapes. The most common ones are rectangular and circle-shaped mazes.
Typically, a maze has a defined start and endpoint with a single way from the start to the end. However, there might be multiple endpoints, multiple starting points, and more than one possible path from the start to the end.
A maze can also have disconnected areas, which means there is no path from the rest of the maze to that area.
A maze where every point is reachable and where there is only one single path from one point in the maze to any other point is called a perfect maze. That’s the type of maze we’ll look at in this article.
3. Maze Generation Based on MST
The classical way to generate a perfect maze is a nice practical application of a Minimum Spanning Tree (MST).
In this article, we won’t discuss MSTs in more detail. The reader who isn’t familiar with MSTs can read more on that topic in our articles on Minimum Spanning Tree Vs Shortest Path Tree and Kruskal’s vs Prim’s Algorithm.
The basis for our maze generation is a graph. The edges of a graph represent a connection between two junctions of a maze.
In the following, we’ll only consider mazes of rectangular shape. However, the underlying graph can be visualized in many different ways.
To generate a maze, we start with a grid (Figure 1). Then we connect every cell with all neighboring cells. Figure 2 shows the resulting connectivity graph in blue:
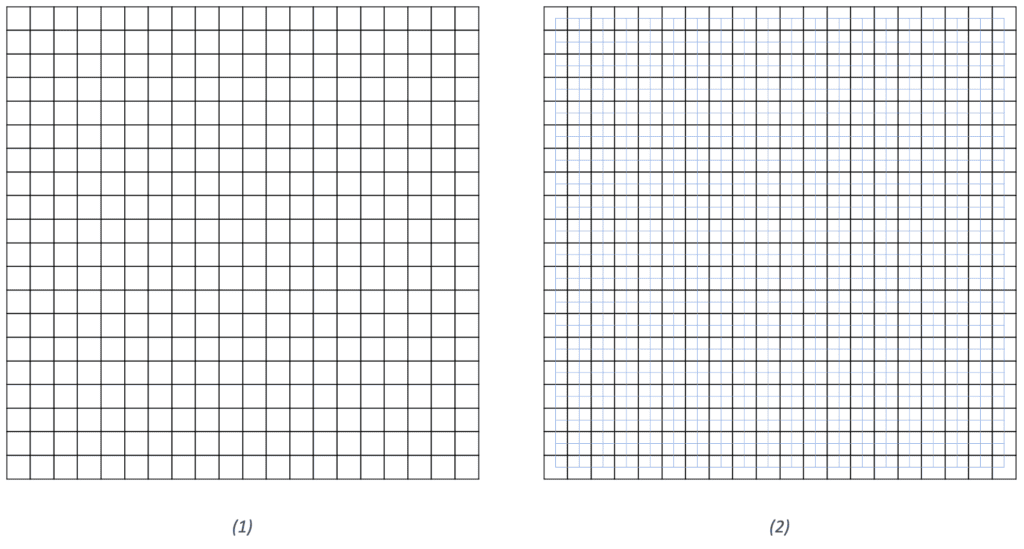
In the next step, we remove the grid and assign random weights to every edge of the graph (Figure 3). Now, we can calculate the MST using an algorithm of our choice. Figure 4 shows an example of an MST based on randomly assigned weights:
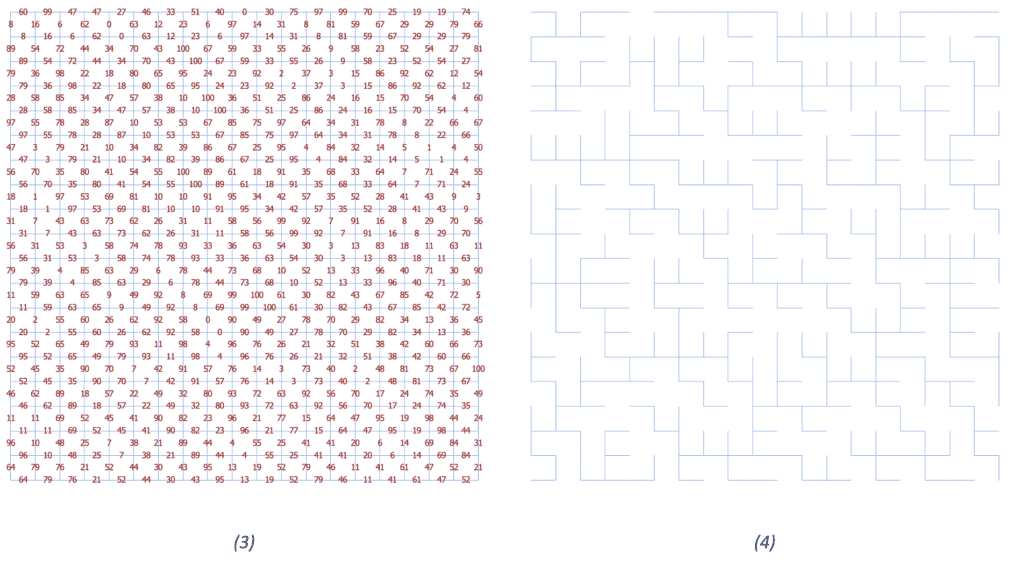
In the last step, we remove all the initial grid walls, which intersect with the MST (Figure 5). The result is a randomized perfect maze (Figure 6):
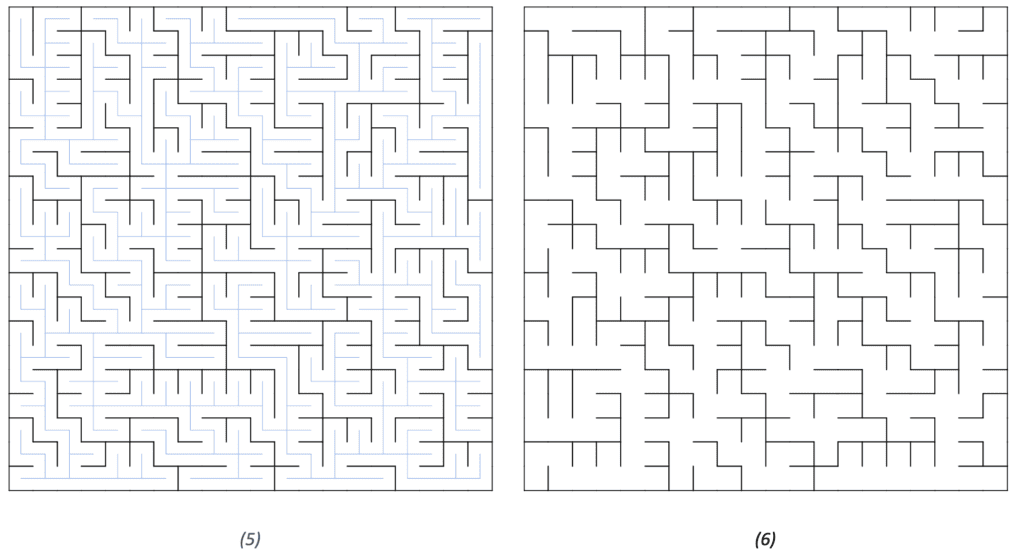
The maze in Figure 6 doesn’t have a single start or end yet. We can choose a random start vertex and a random end vertex, and since an MST has only one path from every cell to any other, the same is also true for our maze.
Furthermore, we can easily calculate the path from a given start vertex to a given end vertex using a shortest-path algorithm like Dijkstra’s Algorithm. Figures 7 and 8 show the path from the bottom left to the top right and top left, respectively:
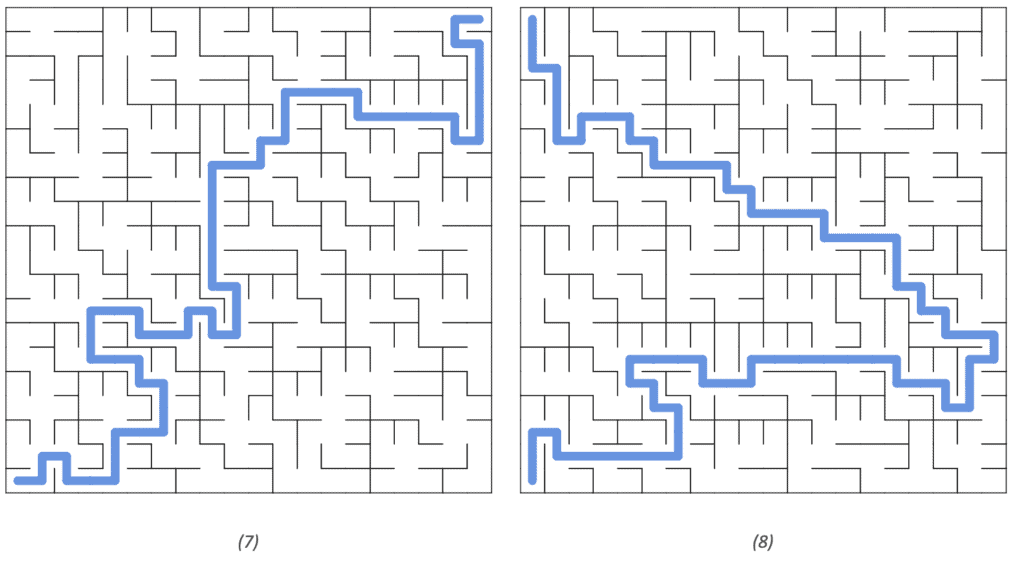
We get an interesting variation if we consider the MST itself as walls as well. Figure 9 shows an example (the vertices of the MST are shown in red). This maze has one single path which forms the entire maze.
That means if we start at any point and follow the maze (there’s no branching), we end up at the same point and have traversed the whole maze:

4. Maze Generation Based on Randomized DFS
4.1. Description
Another way of generating a maze is by applying a randomized Depth First Search (DFS) to the grid.
The algorithm starts at a given cell and marks it as visited. It selects a random neighboring cell that hasn’t been visited yet and makes that one the current cell, marks it as visited, and so on.
If the current cell doesn’t have a neighbor that hasn’t been visited yet, we move back to the last cell with a not-visited neighbor.
The algorithm finished when there is no not-visited cell anymore.
Here is the outline of the algorithm:
The algorithm is recursive and might cause memory issues for big mazes. However, it can easily be implemented as an iterative algorithm similar to the normal DFS.
4.2. Example
The animation shows the current cell in red. Note how the jumps become bigger the more cells are part of the maze:
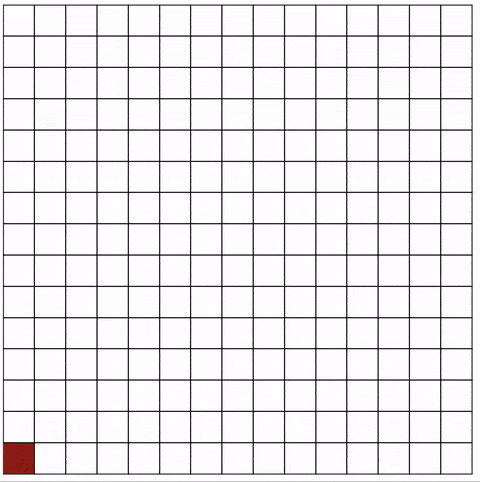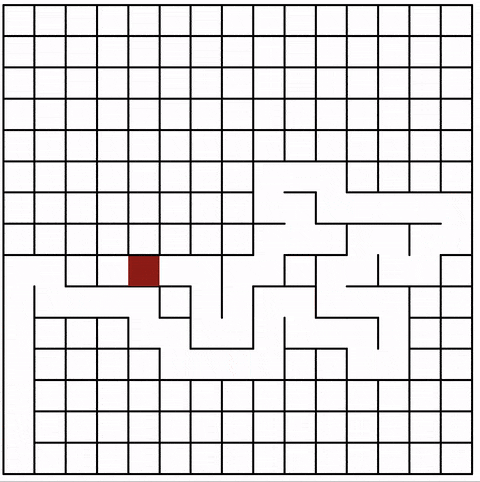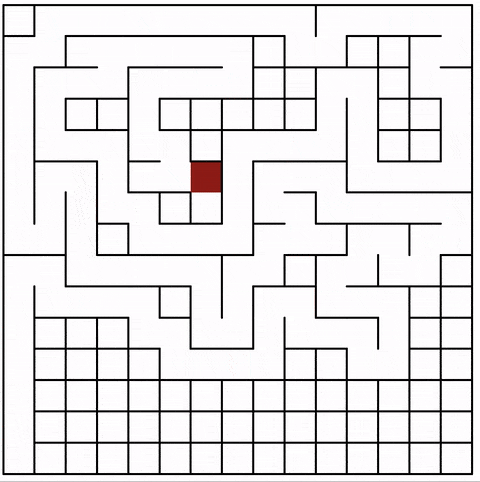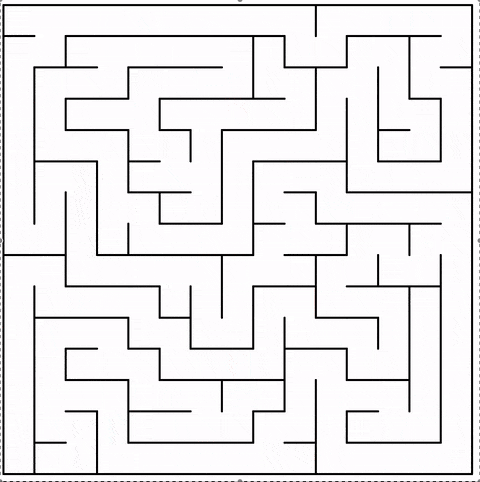
5. Conclusion
We’ve seen two different ways of creating a perfect maze, a randomized MST and a randomized DFS.
There are many ways to visualize a maze. Still, the underlying data structure is always a graph, which means that we can apply graph theory theorems to analyze maze generation and pathfinding in a maze.
Overall, mazes are a fun and practical way to explore graph theory.