Find the Kth Smallest Element in a Binary Search Tree

1. Introduction

In this tutorial, we’ll show how to find the -th smallest element in a binary search tree.

2. The -th Smallest Element

Let’s suppose that a binary search tree has elements: . We want to find the -th smallest. Formally, if is the sorted permutation of , we want to find for the given .

Let’s take this tree as an example:

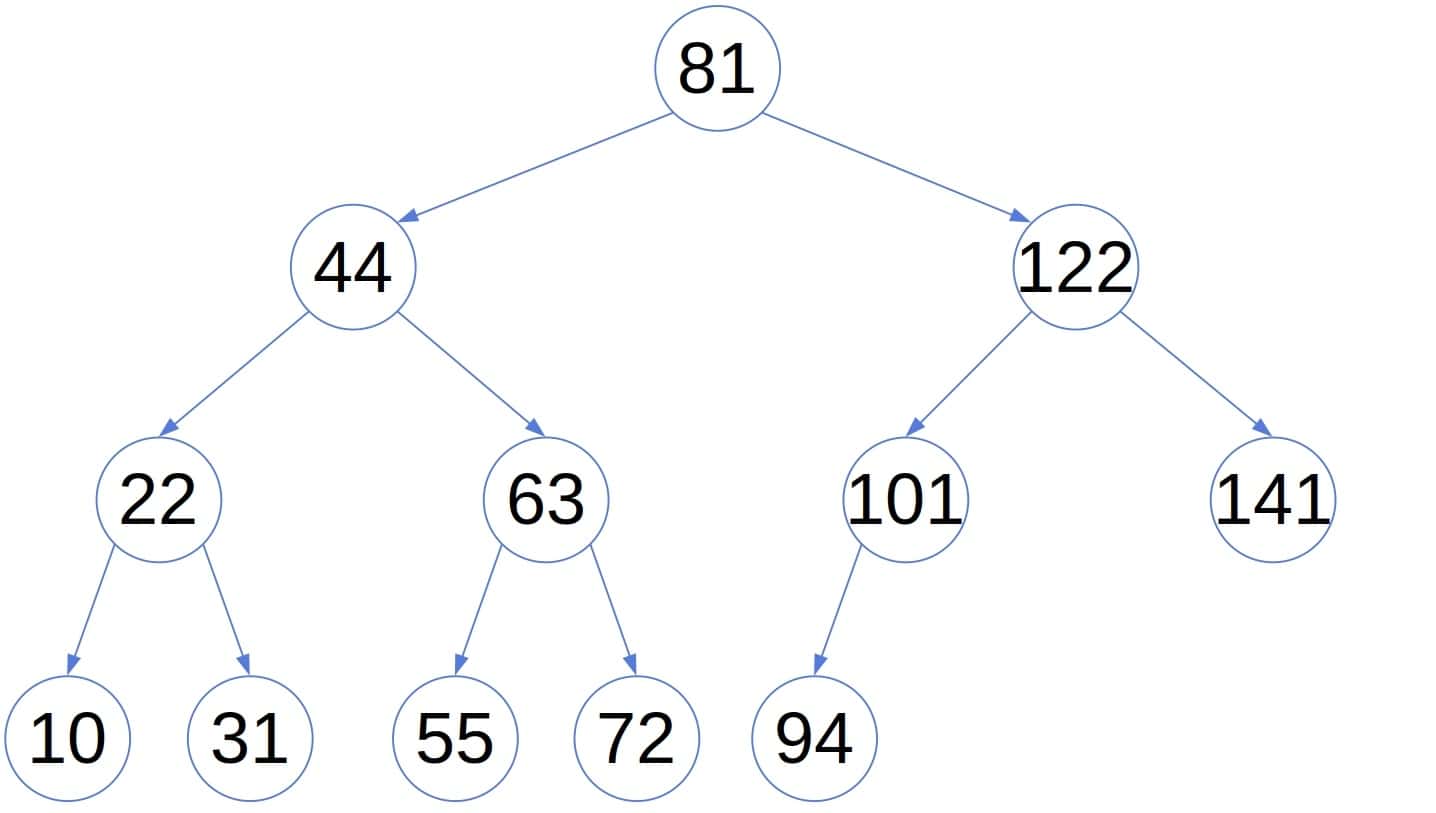
It’s a binary search tree as each node’s value is lower than the values of its right descendants and greater than or equal to those in its left sub-tree. For instance, let . Here’s the fifth smallest number in the tree:

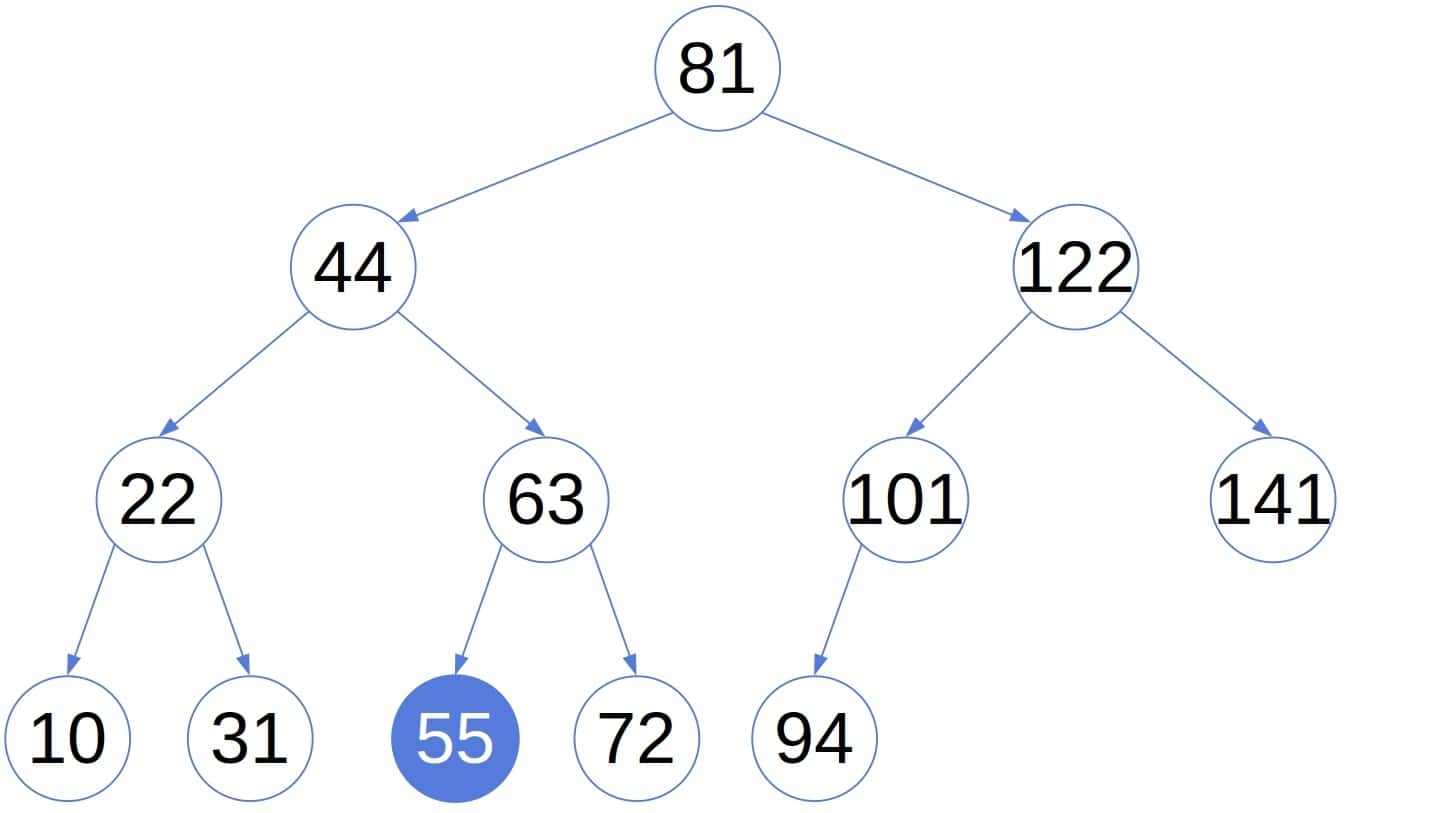
3. Finding the -th Smallest Element With the In-Order Traversal

Since the in-order traversal of a tree outputs its elements in sorted order, we could run the traversal until we get elements. At that point, we can stop because we’ve got the element we wanted:

algorithm findKthSmallestElementInOrder(T, k):
    // INPUT
    //    T = the tree to traverse
    //    k = the rank of the element we want to find
    // OUTPUT
    //    The k-th smallest element in the tree or null if the tree has fewer than k nodes.

    m <- 0
    for x in TRAVERSE-IN-ORDER(T.root):
        m <- m + 1
        if m = k:
            return x
    
    return null

function TRAVERSE-IN-ORDER(x):
    if x.left != null:
        TRAVERSE-IN-ORDER(x.left)
    yield x
    if x.right != null:
        TRAVERSE-IN-ORDER(x.right)

We used the traversal procedure as an iterator, hence the keyword yield. Of course, a fully recursive algorithm would work too.

3.1. Complexity

This approach will work on every binary search tree but is of linear time complexity. For , the algorithm traverses the whole tree to get to the largest element.

4. Finding the -th Smallest Element by Jumping Over Sub-Trees

We can find the -th smallest element more efficiently if we store into each node the number of its descendants. For instance:

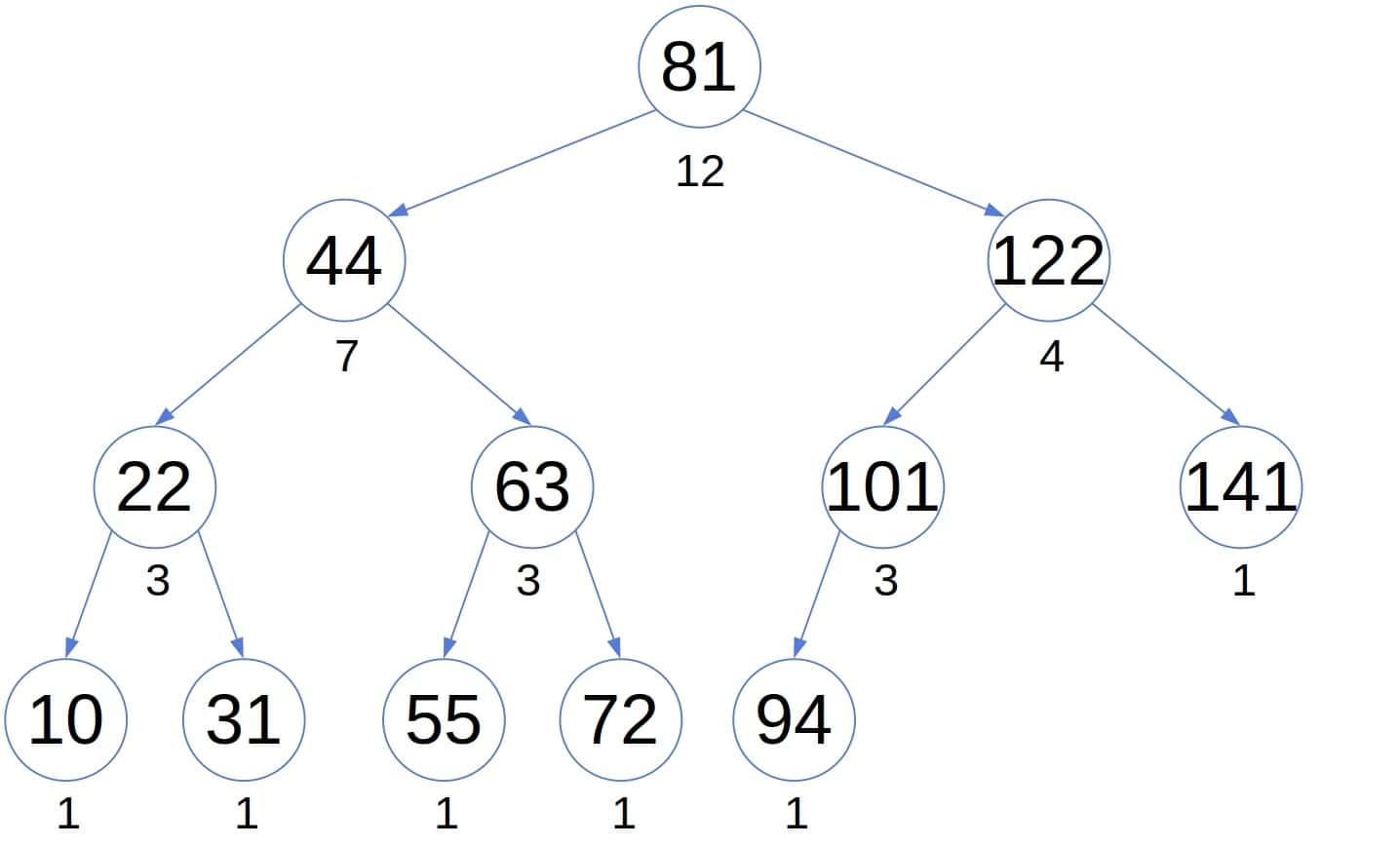
The additional information can speed up the (in-order) traversal. If we visit nodes before , and the ‘s left sub-tree has nodes, then we can skip traversing it if . Why? Because we can be sure that the -th smallest element isn’t in the sub-tree. So, it’s safe to “jump” over it. In doing so, we distinguish two cases. If , then is the -th smallest element in the tree. If , we can skip and go straight to the right sub-tree.

Conversely, if , the -th smallest element is certainly in the left sub-tree.

4.1. Pseudocode

Here’s the pseudocode:

algorithm JUMP-TRAVERSE(x, k, m):
    // INPUT
    //    x = the node we've reached (initially, the tree's root)
    //    m = the number of nodes we visited before calling the function with x as its argument
    //    k = the rank of the element we want to find
    // OUTPUT
    //    the k-th smallest element in the tree
    
    if x.left = null:
        l <- 0
    else:
        l <- x.left.size

    if m + l >= k and x.left != null:
        return JUMP-TRAVERSE(x.left, k, m)
    else if m + l = k - 1:
        return x
    else if m + l < k - 1 and x.right != NULL:
        return JUMP-TRAVERSE(x.right, k, m + l + 1)

At the start, we can test if to check if the element exists.

4.2. Example

To show the efficiency of the modified traversal, let’s check how many nodes it visits in the above tree before finding the fifth smallest element:

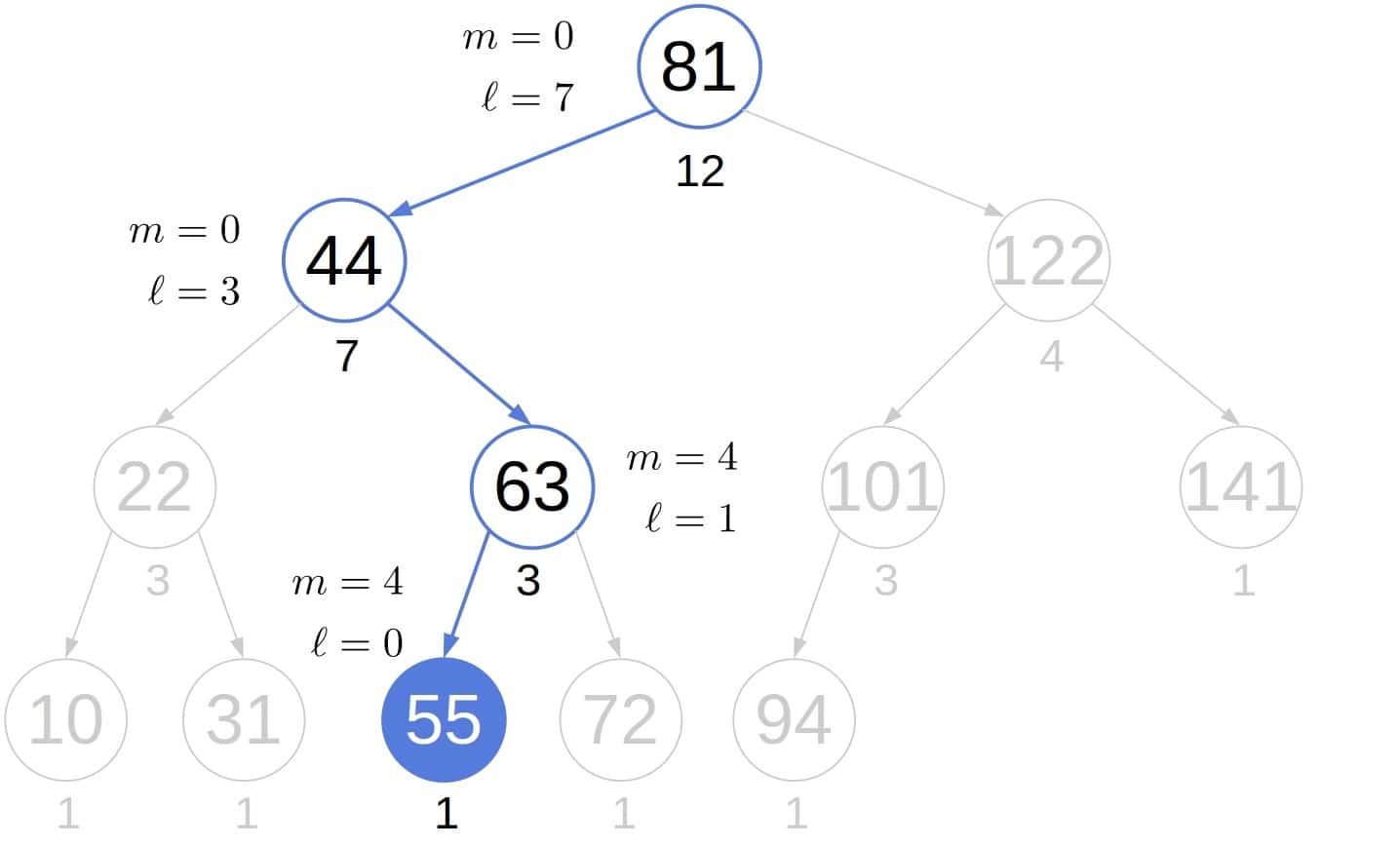
In contrast, the usual in-order search visits all the nodes in the left sub-tree we jumped over:

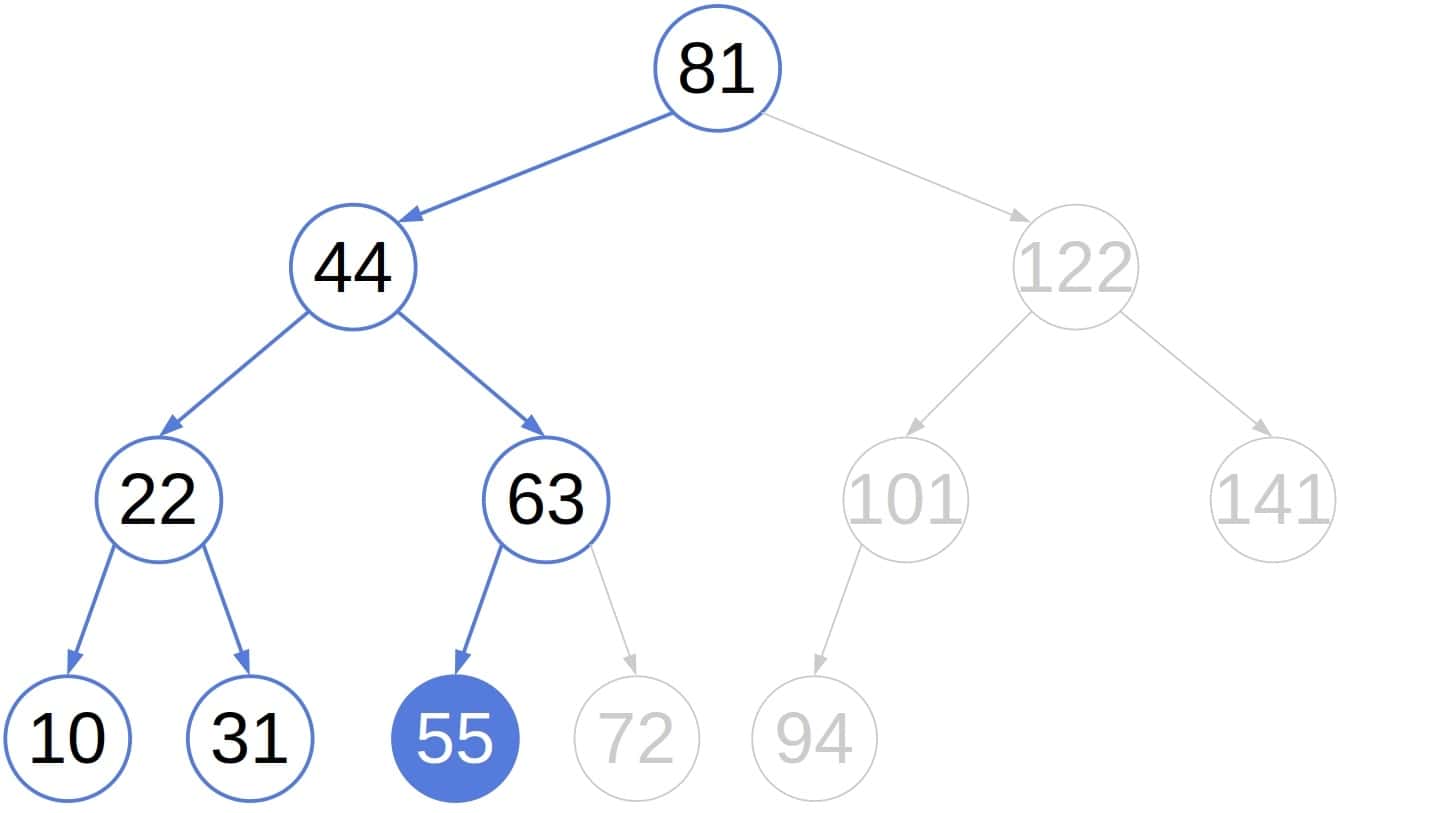
4.3. Complexity

In the worst case, the sub-trees we jump over are the smallest possible. This situation happens if and each node in the tree has only the right child. Such a tree is essentially a linked list. We jump over zero nodes at each step, traversing in total.

In general, each node whose child we jump over is on the path from the root to the node containing the sought value. So, this algorithm’s worst-case time complexity is , where is the tree’s height, i.e., the longest path from the root to a leaf. If the tree is balanced, , so the algorithm has a logarithmic complexity. Without the additional information on the sizes of the sub-trees, the ordinary traversal would have an runtime even if the tree was balanced.

However, since balancing trees adds computational overhead, this approach pays off only if look-ups are more frequent than insertions and deletions. The ideal use-case for this algorithm is the search tree we build once and don’t change afterward.

5. Conclusion

In this article, we showed how to find the -th smallest element in a binary search tree. We can use the usual in-order traversal, but it has an complexity. Keeping the size of each sub-tree in its root allows for a more efficient approach if we use balanced trees.