1. Introduction
In this tutorial, we’ll learn about balanced binary trees.
In particular, we’ll see why such trees come in handy and explore three types of them. We’ll talk about the AVL trees, the red-black trees, and weight-balanced trees. Each type has its definition of balance.
2. Binary and Binary Search Trees
We call a tree binary if each node in it has at most two children. A node’s left child with descendants forms the node’s left sub-tree. The definition of the right sub-tree is similar.
Although suitable for storing hierarchical data, binary trees of this general form don’t guarantee a fast lookup. Let’s take as the example the search for number 9 in the following tree:
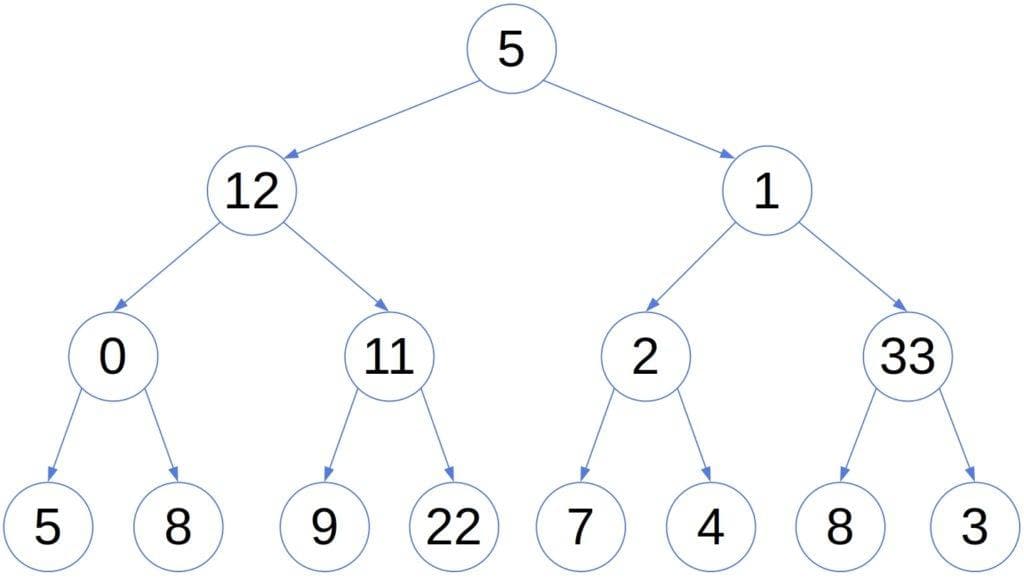
Whichever node we visit, we don’t know if we should traverse the left or the right sub-tree next. That’s because the tree hierarchy doesn’t follow the relation .
So, in the worst case, a search takes time, where
is the number of nodes in the tree.
2.1. Binary Search Tree
We solve this problem by turning to a special type of binary tree called binary search tree (BST). For each node in a BST, all the nodes in the left sub-tree of
contain the values that are strictly lower than
. Further, all the nodes in the
‘s right sub-tree are
. For instance:
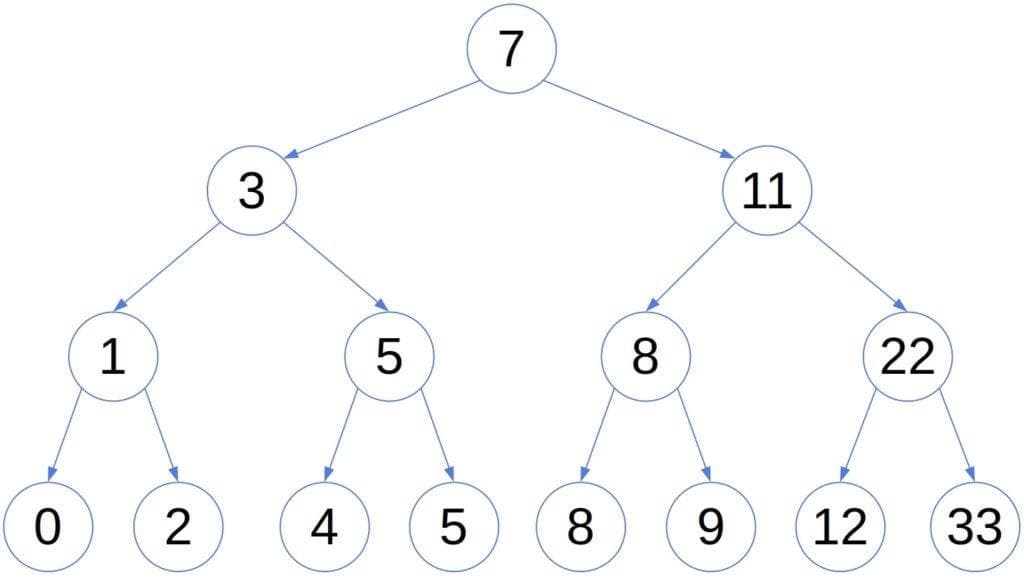
The order the tree maintains allows us to prune it during a lookup. Suppose we visit the node while searching for
. We can disregard the
‘s left sub-tree and focus only on the right, which speeds up the search. This is how we find 9 in the above search tree:
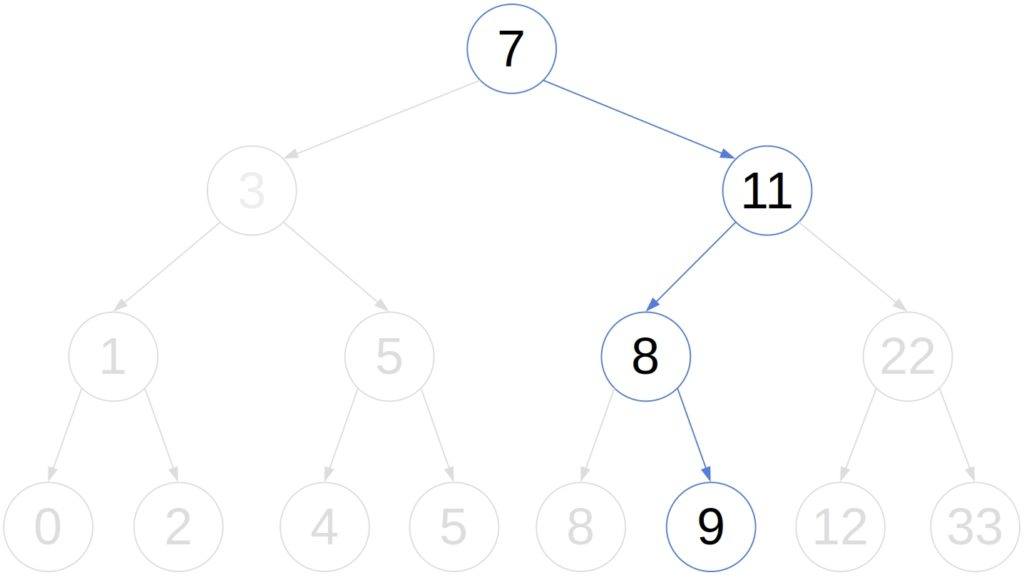
However, the worst-case complexity of the search is still . It occurs if we construct the tree from a sorted array, in which case the tree has height
and degenerates to a linked list. Since insertion and deletion include the search, all operations commonly performed on a BST are
in the worst case. So, it’s the height of the tree that determines the complexity. That’s where balanced trees come in. They’re a special type of binary search tree.
3. Balanced Trees
A balanced tree is a search tree that doesn’t just maintain the order between nodes. It also controls its height, making sure it stays after insertion or deletion.
To do that, a balanced tree must re-balance itself after we add or delete a node. That causes a computational overhead and complicates the algorithms for insertion and deletion. However, that’s the price we’re ready to pay for a logarithmic-height search tree with fast search, insertion, and deletion operations. We won’t cover the re-balancing algorithms in this article.
There are several types of such trees. They require all their nodes to be balanced, but the notion of balance differs from type to type.
4. AVL Trees
In an AVL tree, we call a node balanced if the heights of its left and right sub-trees differ at most by 1. So, a search tree with root is an AVL tree if all its nodes are balanced in the AVL sense (empty search trees, with height 0, are trivially balanced):
(1)
For example:
A consequence of this definition of balance is that an AVL tree’s height is in the worst case.
4.1. Proof That Height Is Logarithmic
An AVL tree is balanced the least if the heights of all the sibling sub-trees differ by one. For instance:
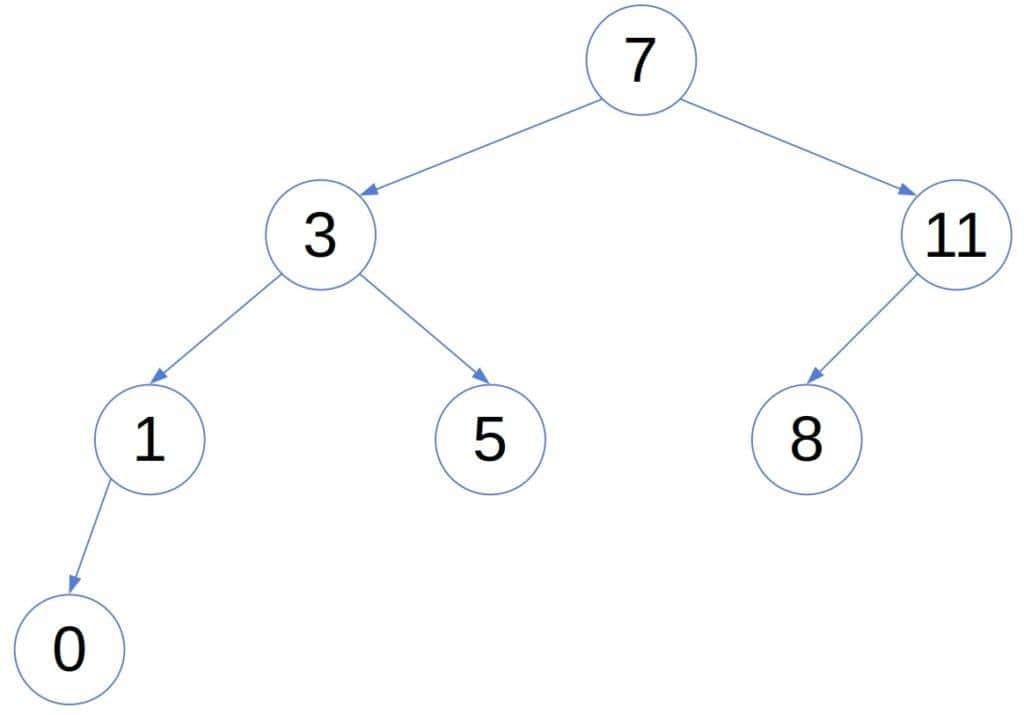
That’s the worst-case structure of an AVL tree. Adding a node to a least-balanced AVL tree, we either get a non-AVL tree or balance one of its nodes. The same goes for deleting a node. So, such AVL trees are minimal: no AVL tree of the same height has fewer nodes.
Even if we switch the node’s left and right sub-trees, the tree will remain balanced. So, we’ll assume that the left sub-trees have more nodes. Then, if is the number of nodes of a minimal AVL tree with height
, we have:
From our assumption, we have that , so:
An AVL structure with height has only one node, so
, and:
Therefore, in the worst-balanced case, an AVL tree’s height is . Hence, the operations such as search, insertion, and deletion have logarithmic time complexity.
5. Red-Black Trees
The Red-Black Trees (RBTs) also balance the sibling subtrees’ heights. But, an RBT differentiates between two types of nodes: the red ones and the black ones. An RBT ensures that all the paths from a node to its descendant leaves to pass through the same number of black nodes. Also, the number of black nodes from a node to its leaves, excluding the node, is called the node’s black height. The black height of the whole RBT is the black height of its root. For example (with NULL leaves coalesced into a single node to save space):
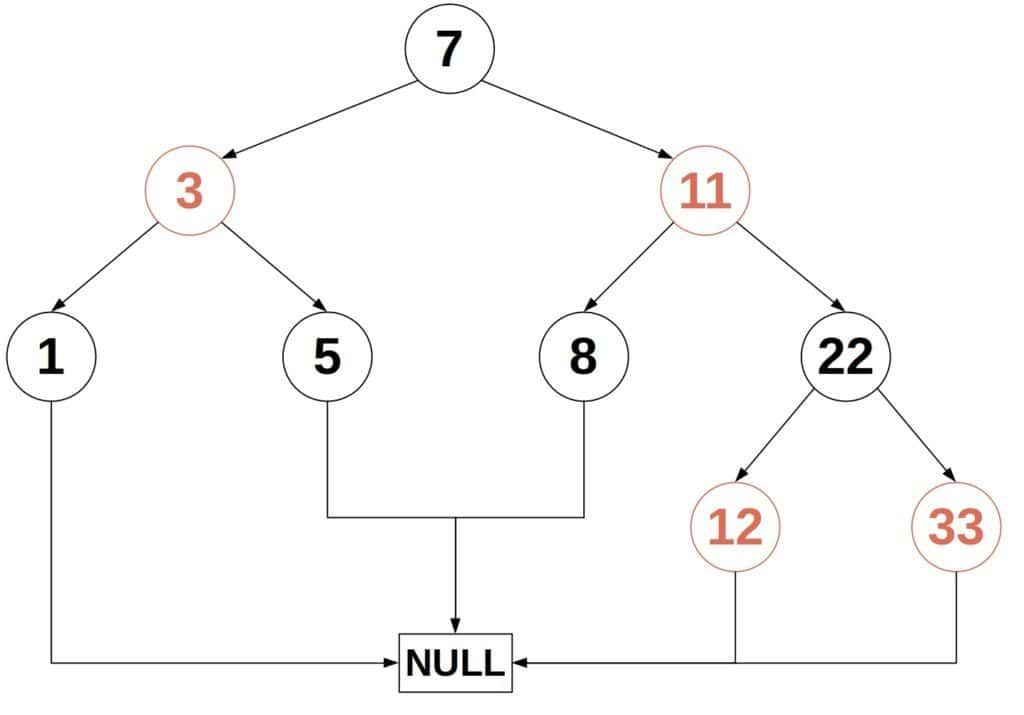
By definition, an RBT fulfills these conditions:
- Every node is either black or red.
- The root is black.
- Every empty node (NULL or NIL) is black.
- If a node is red, then both its children are black.
- For every node
, the paths from
, not including it, to its descendant leaves contain the same number of black nodes.
Some authors don’t require the root to be black because we can repaint a tree in any case.
The properties of an RBT ensure:
- that no path from the root to a leaf is more than twice as long as a path to another leaf,
- and that the tree’s height is
.
5.1. Proof That the Height of an Rbt Is 
Let be the black height of
. We’ll first prove, by induction, that a sub-tree rooted at
has at least
internal nodes.
The base case is , which means that
is an empty node, that is, a leaf:
So, we’ve covered the base case. In the inductive step, we focus on and its children. Their black heights are equal to
or
, depending on their colors. By the hypothesis, they contain at least
nodes each. So, the whole tree rooted at
contains this many nodes at a minimum:
Now, let be the height of the root node
. Since red nodes can have only black children, at least half of the nodes from the root to any leaf must be black. Therefore, the root’s black height is
.
Using the result about the internal nodes, we get:
Again, we get that the height grows as the logarithm of the number of nodes.
6. Weight-Balanced Trees
The weight-balanced trees (WBTs) don’t balance the heights of the sibling sub-trees, but the numbers of leaves in them. So, let and
be the sub-trees of
and let
. We say that
is balanced if:
We also require all the descendants of to fulfill the same condition. This is equivalent to stating that there exists an
such that the following holds for every node
in the tree:
To see why, let’s remember that and follow the derivation:
So, this is the recursive definition of a WBT :
(2)
Here’s an example of a WBT with (the number of leaves is written inside each node):
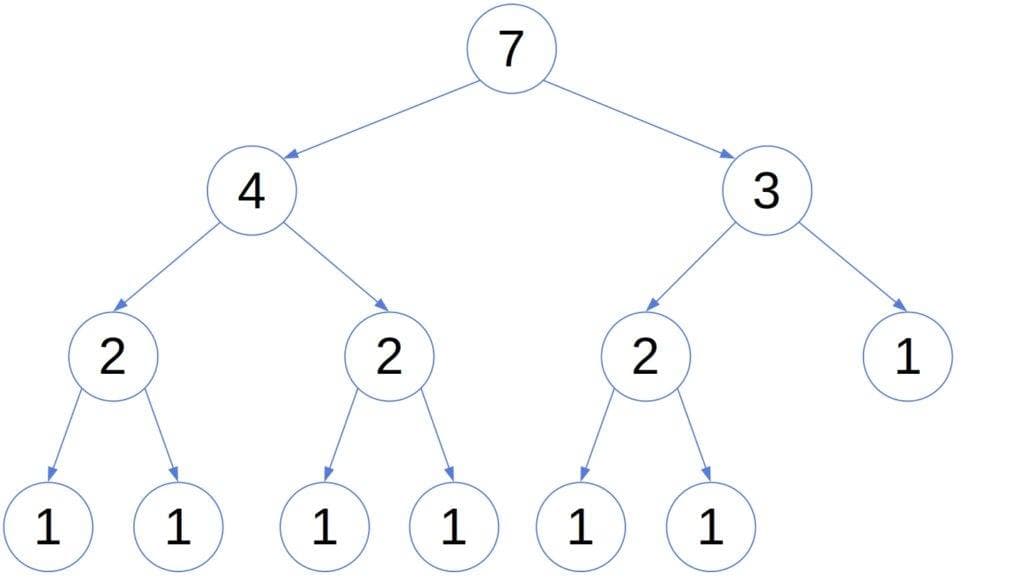
The number of leaves in the tree is its weight, hence the name. We’ll prove that the height of a WBT is also bounded by .
6.1. Proof That the Height of a Weight-Balanced Tree Is 
Let’s suppose that is a minimal WBT whose height is
, and let
denote the number of leaves in it. From the definition of a WBT, we see that a sub-tree of
contains at most
of the node’s leaves. Also, a subtree’s height is at most
. So, we have:
Since , where
is the number of nodes in the tree, we have:
So, the height of a WBT is also logarithmic in the number of nodes.
6.2. The Value Of 
If we use a too large , re-balancing may become impossible. Its value should be
.
If we’re ready to use a complicated custom re-balancing algorithm, we can use an arbitrarily small . However, the recommendation is to use
.
7. Conclusion
In this article, we presented three types of balanced trees. Those were: the AVL trees, red-black trees, and weight-balanced trees. Using different notions of balance, they all guarantee the time complexity of search, insertion, and deletion.
However, the trees have to re-balance themselves upon change so that their height stays logarithmic in the number of nodes. The additional work complicates and slows down the algorithms for insertion and deletion. But, the overhead pays off because the complexity of the operations remains .