1. Introduction
In this tutorial, we’ll explain what an induced subgraph is. We’ll also show how to construct it, how to check if a (sub)graph is induced, and how to find the induced graph isomorphism.
2. Subgraphs
Let’s say we have a graph , where
is the set of nodes, and
denotes the edges between them. A subgraph of
is any graph
such that
and
. In other words, each node in a subgraph is also a node in the supergraph. Further, every edge in the subgraph is an edge in the supergraph.
For example, all these graphs:
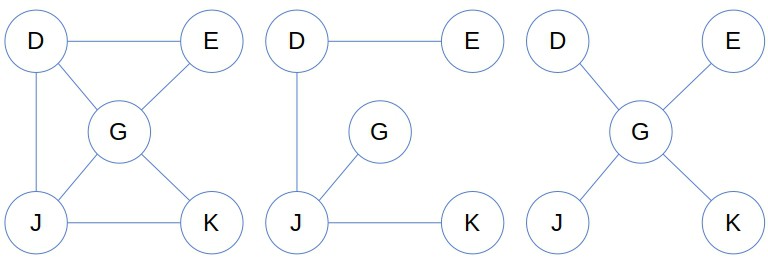
Can be listed as subgraphs of:
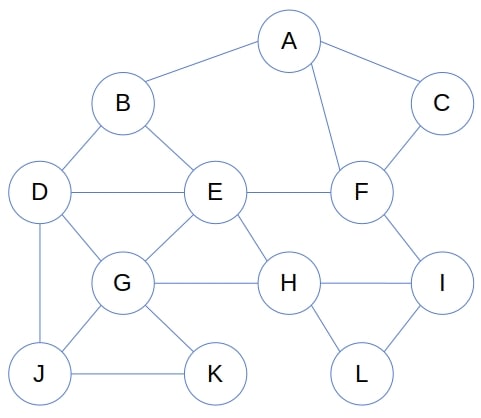
3. Induced Subgraphs
An induced subgraph is a special case of a subgraph. If is a subset of
‘s nodes, then the subgraph of
induced by
is the graph that has
as its set of vertices and contains all the edges of
that have both endpoints in
. This definition covers both directed and undirected graphs. Also, it covers the weighted just as the unweighted ones.
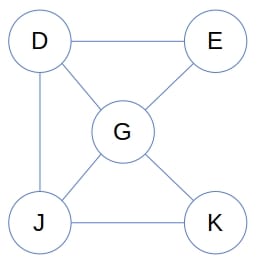
Given and
, the induced subgraph is unique. There’s only one subgraph induced by
in the above graph:
3.1. What’s the Difference?
The concepts of an induced subgraph and an ordinary subgraph are very similar. The difference is that an induced subgraph includes all the edges that have both endpoints in the inducing set , whereas an ordinary subgraph may miss some.
So, an induced subgraph keeps both adjacency and non-adjacency of the inducing vertices, in contrast to an ordinary subgraph that preserves only non-adjacency.
4. Induced Subgraph Problems and Algorithms
Let’s introduce a few problems related to induced subgraphs.
4.1. Induced Subgraph Construction
Here, the input consists of the graph and the inducing set
. Our goal is to construct the induced subgraph
. We’ll do so by iterating over the edges in
and keeping only those whose both endpoints are in
:
The time complexity depends on how we represent the graphs. Using linked lists, we traverse each edge incident to a node in twice, so the time complexity is
. On the other hand, if we use matrices, we traverse the whole row of
entries for each of the
inducing nodes. Therefore, the complexity will be
.
4.2. How to Check if a Subgraph Is Induced
In this problem, we have a graph and its subgraph
(so
and
). Our goal is to check if
is an induced subgraph of
. To do so, we iterate over the edges incident to
in
. If we find an edge that isn’t in
, we can conclude that
isn’t an induced subgraph because it doesn’t preserve adjacency. Otherwise, we conclude that
is induced:
As before, the complexity depends on the way we represent the graphs.
We don’t need to check if contains an edge not in
. That’s because of the way we defined the input. Since we know that
is a subgraph of
,
can’t contain an edge that’s not in
.
4.3. How to Check if a Graph Is an Induced Subgraph
However, if we get as a graph of some nodes in
, we’ll have to check both that
is a subgraph and that it is induced.
4.4. Induced Subgraph Isomorphism
The Induced Subgraph Isomorphism (ISI) is an injective mapping from one graph to an induced subgraph of another,
. So, we get
and
at the input and find an ISI mapping from the former to the latter.
Unlike in the previous two problems, and
don’t use the same labels for their nodes. So, we have to find a mapping that translates
to an induced subgraph of
:
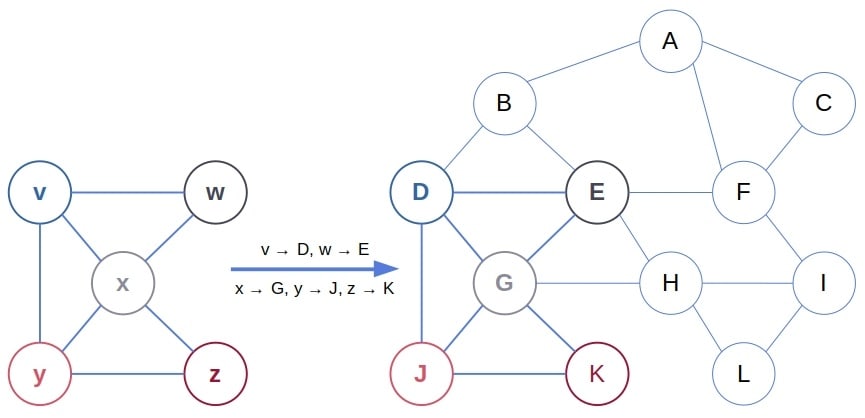
Formally, we say that is an ISI if and only if it satisfies:
(1)
The first condition states that is an injective function. The second is that an ISI preserves adjacency, and the third is that it also keeps non-adjacency.
This problem is NP-hard, which means that no polynomial-time algorithm for solving it is known to date. We can treat it as a constraint-satisfaction problem (CSP) and solve it like we solve other CSPs. The Equation (1) lists all the constraints we need to define the CSP and feed it to the universal solver. Each for
will correspond to a CSP variable, and each variable will have the whole set
as its domain.
5. Conclusion
In this article, we talked about induced and ordinary subgraphs. We also presented a few common problems related to the former subgraphs. Those are the induced subgraph construction, verification, and isomorphism.