Roulette Selection in Genetic Algorithms

1. Overview

In this tutorial, we’ll study the roulette wheel selection method for genetic algorithms.

2. Genetic Algorithms

The selection of chromosomes for recombination is a mandatory step in a genetic algorithm. The latter is, in turn, an algorithm that’s inspired though not reducible to the evolutionary process of biological species.

Genetic algorithms find important applications in machine learning. For example, we use them in the selection of policies in reinforcement learning. But also, in the optimization of parameters for deep learning, in the subset sum problem, in pathfinding, or, in general, in the solution to many search problems in reasoning and learning.

The real-world problems that they help solve span from the discovery of new materials to the identification of biomarkers in computational biology. But also, the disease screening and drug discovery in medicine. Therefore, they’re important tools in the toolbox of any data scientist.

For genetic algorithms to work as intended, it’s necessary however to solve the related problem of recombination between chromosomes first.

3. Recombination

A typical definition of a chromosome considers it as a fixed-length array that contains a binary variable:

Each bit of the variable then maps to a parameter or characteristic of some type. In this manner, we can describe an individual possessing a finite set of binary characteristics exclusively in terms of a chromosome. The chromosome, then, allows the representation of a population that contains as many as different types of individuals.

This lets us represent complex agents composed of multiple subsystems. In the case of policies for reinforcement learning, for example, the chromosome normally corresponds to either the agent’s perceptual system, or its movement controller, or both.

All individuals, each with their own chromosome, start to operate in the environment. As they do, each receives a measure of fitness , according to its performances. Then, after we compute the fitness for all individuals in a population, we proceed with the recombination phase.

During this phase, we select some individuals to act as parents. These parents, in turn, mix their chromosomes according to a procedure called crossover or recombination.

4. Selecting by Fitness

We thus need a method for identifying the parents whose chromosome we subject to recombination:

This method needs to use the fitness of individuals in the population. Or otherwise, there’s no learning between one generation and the next.

There are two main categories of methods for using fitness in order to support selection:

• deterministic methods
• stochastic methods

Deterministic methods involve, for example, the selection of the -most fit individuals in a population for recombination. They’re generally discredited because they tend to develop a population that reaches a local maximum and then stops evolving.

Alternatively, we can also use stochastic methods for selecting parents. The most extreme of these methods select individuals randomly with uniform probability, and thus completely disregards their individual fitness.

A good middle way, instead, is the roulette wheel selection, which creates a discrete probability distribution from which we identify the chromosomes for crossover.

5. Principles of Roulette Selection

Roulette selection is a stochastic selection method, where the probability for selection of an individual is proportional to its fitness. The method is inspired by real-world roulettes but possesses important distinctions from them. As we know from the movies on casinos and gamblings, roulettes always have slots with the same size:

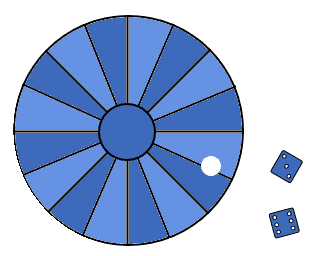
That means, however, that all slots have the same probability of being selected. Instead, we can implement a weighted version of the roulette. With it, the larger the fitness of an individual is, the more likely is its selection:

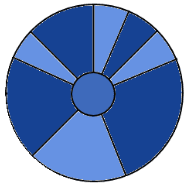
The first component of the roulette selection method is, therefore, that individual fitness is proportional to its likelihood of selection.

This isn’t sufficient though. This is because, if the population has individuals, then the summation of probabilities of their selections equals one. As a consequence, we have to also normalize all values for the individual probabilities to the interval .

6. Roulette Wheel Selection

Finally, we can sum up the considerations made above and develop a method that satisfies the requirements we set.

In a population with individuals, for each chromosome with a corresponding fitness value , we compute the corresponding probability of selection as:

We can then simply treat the probability distribution as the one from which we sample the parents we choose for recombination.

7. Conclusion

In this article, we studied how to perform roulette selection for genetic algorithms.