Genetic Algorithms: Order One Crossover

1. Overview

In this tutorial, we’ll discuss a crossover operator used in genetic algorithms: order one crossover. We’ll present the process of applying this operator with examples.

Finally, we’ll highlight the advantages and disadvantages of this operator.

2. Introduction

Genetic algorithms (GAs) are optimization algorithms based on the principles of natural selection and genetics. Additionally, we utilize them to solve complex optimization problems.

Among all the operations, a crossover is a crucial step in genetic algorithms. Once we select the parents, the GA performs a crossover operation that combines the genetic material of two parent chromosomes to create two new offspring. Additionally, there’re various crossover operators, such as order one crossover, uniform crossover, and two-point crossover.

We use the order one crossover (OX1) in genetic algorithms to generate new candidate solutions from parents’ solutions. Specifically, it’s a useful operator for problems that have a permutation representation.

In OX1, we randomly select a crossover point along with the chromosomes of two parents. Furthermore, we copy the elements between the two points in the first parent to the offspring, preserving their relative order. Additionally, the remaining elements in the offspring are then filled in by the second parent in the order that they appear in the second parent, without repeating any elements already included in the offspring. Similarly, we generate the second offspring using the same process, following a different order of coping the chromosomes from the parents to the offspring.

We mainly use the order one crossover operator in evolutionary algorithms for combining two parent individuals to generate two offspring. Another common application of order one crossover is in solving optimization problems where the goal is to find the values of a set of parameters that optimize some objective function.

3. Working Process

Now, let’s discuss how the order one crossover operator works. It has three major steps:

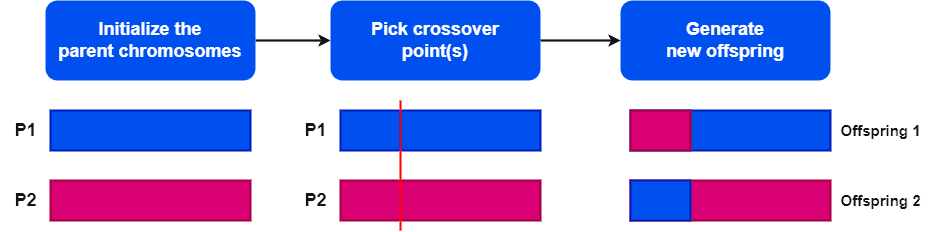
The first step is to select two parent chromosomes from the current population. As soon as we initialize the parent chromosomes, we need to choose a crossover point. Furthermore, we generally pick a random crossover point for simplicity.

The crossover point divides the parent chromosomes into two parts. Now, it’s time to generate the two new offspring. The length of the two new offspring chromosomes is the same as that of the two parent chromosomes. Additionally, the new offspring chromosomes contain two parts in the same way we divide the parent chromosomes.

For the first offspring, we copy the elements of the second parent up to the crossover point index and add them to the corresponding section of the offspring chromosome. Additionally, if there are any remaining positions in the offspring, we need to fill them, as the length of the offspring should be the same as the parent chromosomes.

Hence, we fill in the remaining positions in the offspring with the elements from the first parent chromosome, starting from the crossover point until the end of the sequence. Furthermore, we fill the offspring without duplicating any elements already included in the offspring chromosome. However, if the parent chromosomes contain identical elements, the offspring chromosome will have duplicate elements.

Finally, we add the two new resulting offspring to the next-generation population. By using OX1, the offspring chromosome contains genetic material from both parent chromosomes, allowing for the creation of new candidate solutions that may not have been present in the initial population.

4. Example

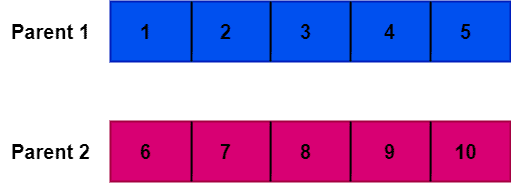
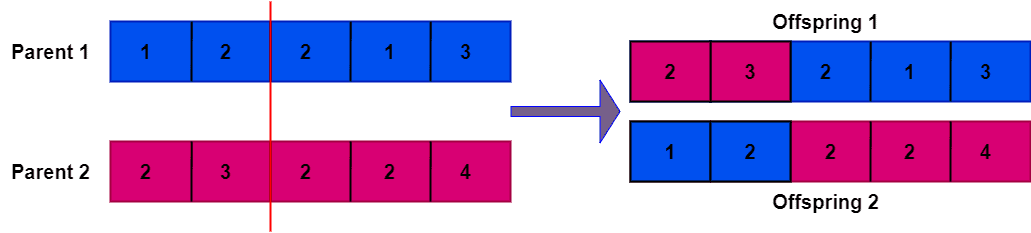
Now, let’s take an example to illustrate how OX1 works. First, we’re taking two parent chromosomes to apply the order one crossover operator to them:

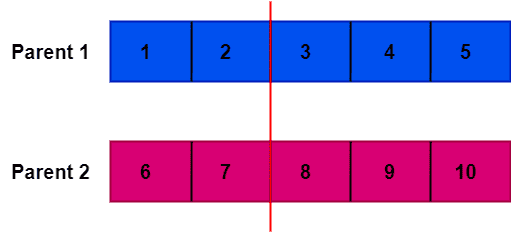
Now, we need to choose a random crossover point. In our example, we pick index 2 as a crossover point. The crossover point divides the parent chromosomes into two sections:

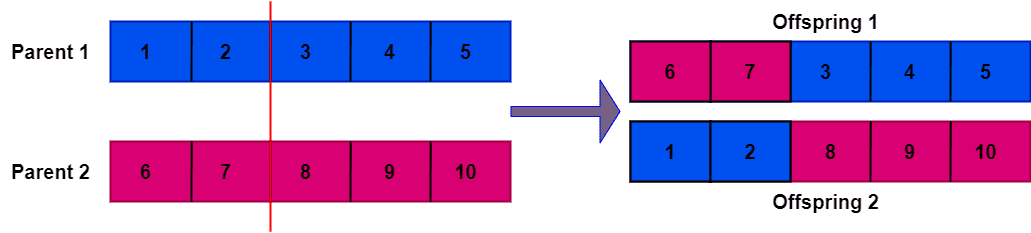
Moving forward, we copy the elements up to the crossover point of Parent 2 into the first offspring. Similarly, we fill the second part of the offspring with the elements, starting from the crossover point until the end of Parent 1. We follow the same approach for the second offspring. However, in this case, we start coping from Parent 1, followed by Parent 2.

While filling in the remaining elements in the offspring, it’s important to remember that no duplicate element is allowed if each parent contains unique elements. Let’s take a look at the two new offspring generated from the parent chromosomes:

However, if the parent chromosomes contain identical elements, the offspring will have duplicate elements. Let’s take a look at an example where parent chromosomes contain identical repetitive elements:

Additionally, the newly generated population isn’t unique. Based on the crossover point and the elements that need to be preserved, we can generate multiple new populations from parent chromosomes.

5. Implementation in Python

Let’s discuss the implementation details of the order one crossover operation in genetic algorithms using Python.

5.1. Importing Libraries

Before we start implementation, the first step is to import the required libraries:

import random

The random library in Python is used for various tasks, such as random number generation and random selection of elements. Furthermore, we use the random library to introduce randomness in our programs.

5.2. Defining the Main Function

Furthermore, we define a function for the implementation of the order one crossover operation:

def order1_crossover(p1, p2, cross_point):
    return newp1, newp2

Here, we provide two parent chromosomes and as input. Furthermore, the function performs some calculations and returns the two new offspring chromosomes: , .

5.3. Statements Within the Main Function

Given and , first, let’s determine the length of the parent chromosomes:

length1 = len(p1)
length2 = len(p2)

As we mentioned before, the length of the parent chromosomes must be the same to apply the order one crossover operation. Hence, we compare the length of the parent chromosomes before moving forward with the implementation:

if length1  != length2:
    raise ValueError("The size of the parent chromosomes are different")

The size of the two new offspring chromosomes would be the same as the parent chromosomes. Hence, let’s create and initialize the offspring chromosomes:

newp1 = [0] * length1
newp2 = [0] * length2

The next step is to pick a crossover point. Thus, we’re going to choose the crossover point randomly. Random selection ensures that the crossover point is neither at the beginning nor the ending of the parents. Therefore, we generate offspring that are different from the parent chromosomes:

cross_point = random.randint(0, length1 - 2)

Now, we’re ready to start the order one crossover operation. First, we start coping elements from the parent chromosomes to the offspring from the crossover point until the end of the sequence:

for i in range(cross_point, length1):
    newp1[i] = p1[i]
    newp2[i] = p2[i]

Furthermore, let’s fill the remaining positions:

for i in range(cross_point):
    if p1[i] not in newp1:
        newp1[i] = p2[i]
    if p2[i] not in newp2:
        newp2[i] = p1[i]

When filling is done, we return the two new offspring chromosomes.

5.4. The Complete Code

Let’s take a look at the complete code:

import random
def order1_crossover(p1, p2, cross_point):
    length1 = len(p1)
    length2 = len(p2)
    if length1 != length2:
        raise ValueError("The size of the parent chromosomes are different")
    newp1 = [0]*length1
    newp2 = [0]*length2
    for i in range(cross_point, length1):
        newp1[i] = p1[i]
        newp2[i] = p2[i]
    for i in range(cross_point):
        if p1[i] not in newp1:
            newp1[i] = p2[i]
        if p2[i] not in newp2:
            newp2[i] = p1[i]
    print("Offspring 1:", newp1)
    print("Offspring 2:", newp2)    
    return newp1, newp2

Now, we provide the parent chromosomes and the crossover point as input. Finally, we call the main function:

p1 = [1, 2, 3, 4, 5]
p2 = [6, 7, 8, 9, 10]
cross_point = random.randint(1, len(p1) - 2)
try:
    newp1, newp2 = order1_crossover(p1, p2, cross_point)
except ValueError as e:
    print(e)

In this case, we pick index 2 as a crossover point. After running the code, we get two offspring as output:

Offspring 1: [6, 7, 3, 4, 5]
Offspring 2: [1, 2, 8, 9, 10]

6. Advantages

There are several advantages of using order one crossover (OX1) in genetic algorithms (GAs). In particular, some of the vital benefits are the maintenance of the diversity of chromosomes, simplicity, and preservation of important elements in chromosomes.

OX1 allows the creation of offspring chromosomes containing genetic material from both parent chromosomes. Hence, it helps to maintain diversity in the population and prevents the GA from getting stuck in local optima.

Additionally, OX1 is a simple and easy-to-implement crossover operator. Thus, it only requires the selection of a single crossover point and doesn’t require complex calculations or operations.

Finally, it ensures that important elements in the parent chromosomes are preserved in the offspring chromosomes. This is because the first section of one parent chromosome is always copied into the offspring chromosome, ensuring that at least some of the genetic material from that parent is preserved.

Overall, OX1 is a simple and effective crossover operator that can help maintain diversity in the population and produce high-quality candidate solutions.

7. Disadvantages

OX1 is a popular and effective crossover operator in genetic algorithms (GAs). However, there’re also some disadvantages and limitations associated with its use. Some of the drawbacks of the OX1 operator are limited exploration, premature convergence, and ineffectiveness for non-permutation problems.

OX1 can be limited in its ability to explore the search space. This is because it only creates offspring chromosomes by exchanging genetic material between two parent chromosomes. Furthermore, it doesn’t introduce new genetic material from outside the current population, which could be useful in exploring new regions of the search space.

Additionally, it can sometimes lead to premature convergence, where the GA converges to a suboptimal solution too quickly. However, this can happen when the initial population contains a large number of similar or identical chromosomes. In such cases, OX1 may simply recombine genetic material between similar chromosomes, leading to a lack of diversity in the population.

Finally, OX1 is designed specifically for problems that have a permutation representation. It may not be suitable for problems that have a different representation, such as real-valued or binary-coded variables.

8. Conclusion

In this tutorial, we discussed a crossover operator in genetic algorithms: order one crossover. We explored how to apply this operator in order to generate new offspring chromosomes with an example. Furthermore, we also presented the implementation details of the order one crossover operation in Python.

Finally, we highlighted the advantages and disadvantages of this operator.