Learn through the super-clean Baeldung Pro experience:
>> Membership and Baeldung Pro.
No ads, dark-mode and 6 months free of IntelliJ Idea Ultimate to start with.
Last updated: March 18, 2024
In this article, we’ll explain what the term “depth” refers to when it comes to convolutional neural networks. Also, we’ll explain the difference between the depth of the whole neural network and the depth of the convolutional layer.
Neural networks are algorithms explicitly created as an inspiration for biological neural networks. The basis of neural networks are neurons that interconnect according to the type of network. Initially, the idea was to create an artificial system that would function just like the human brain.
There are many types of neural networks, but they roughly fall into three main classes:
For the most part, the difference between them is the type of neurons that form them and how the information flows through the network. In this article, we’ll briefly explain only convolutional neural networks.
Convolutional neural networks (CNN) are a type of artificial neural network, a machine learning technique. They’ve been around for a while but have recently gained more exposure because of their success in image recognition. A convolutional neural network is a powerful tool that we can use to process any data to apply the convolution operation.
The success of CNN is because they can process large amounts of data such as images, videos, and text. Primarily, we can use them to classify images, localize objects, and extract features from the image, such as edges or corners. They’re typically composed of one or more hidden layers, each of which contains a set of learnable filters called neurons.
When it comes to CNN, the term “depth” can be found in the literature in two contexts:
Below, we’ll explain both of the concepts.
Neural Networks consist of layers where each layer has multiple neurons. The number of layers in a neural network defines its depth. Also, a neural network must have at least two layers:
In addition, all layers different from the input and output layers are hidden layers. It’s common that CNN has around five to ten layers, but some modern architectures have up to one hundred layers.
A convolutional layer is a layer where we apply filters to the input images or tensors. We can visualize this process more intuitively by looking at the following figure:
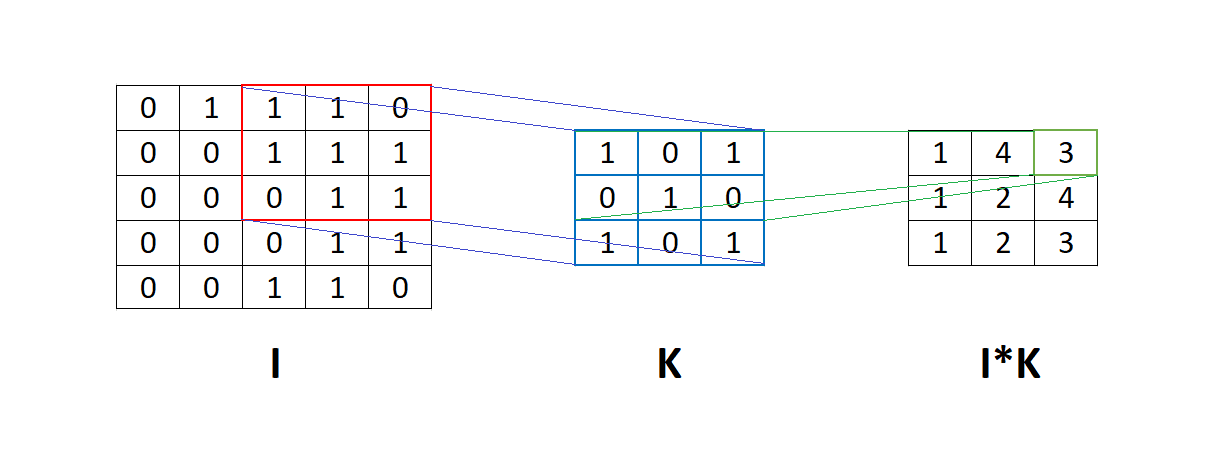
The figure above shows the matrix to apply the convolution using filter
. This means that filter
passes through matrix
, and an element-by-element multiplication is applied between the corresponding element of the matrix
and filter
. Then we sum the results of this multiplication into a number.
Usually, the inputs to the CNN are color images. They consist of the three channels that represent the intensity of red, green, and blue colors. Every pixel in the image combines these three colors, where the intensity of the color is described with an integer number from 0 to 255.
Hence, input images have their width, height, and depth. The depth of the input images defines the depth of the input layer. Consequently, the depth of the second layer depends on the number of kernels we used in the input layer.
For instance, let input image has dimension
and filter or kernel
has dimension
. Notice that the kernel depth must be the same as the depth of the input image. Let the convolution between
and
be matrix
. With a kernel step of one, the matrix
has a dimension
.
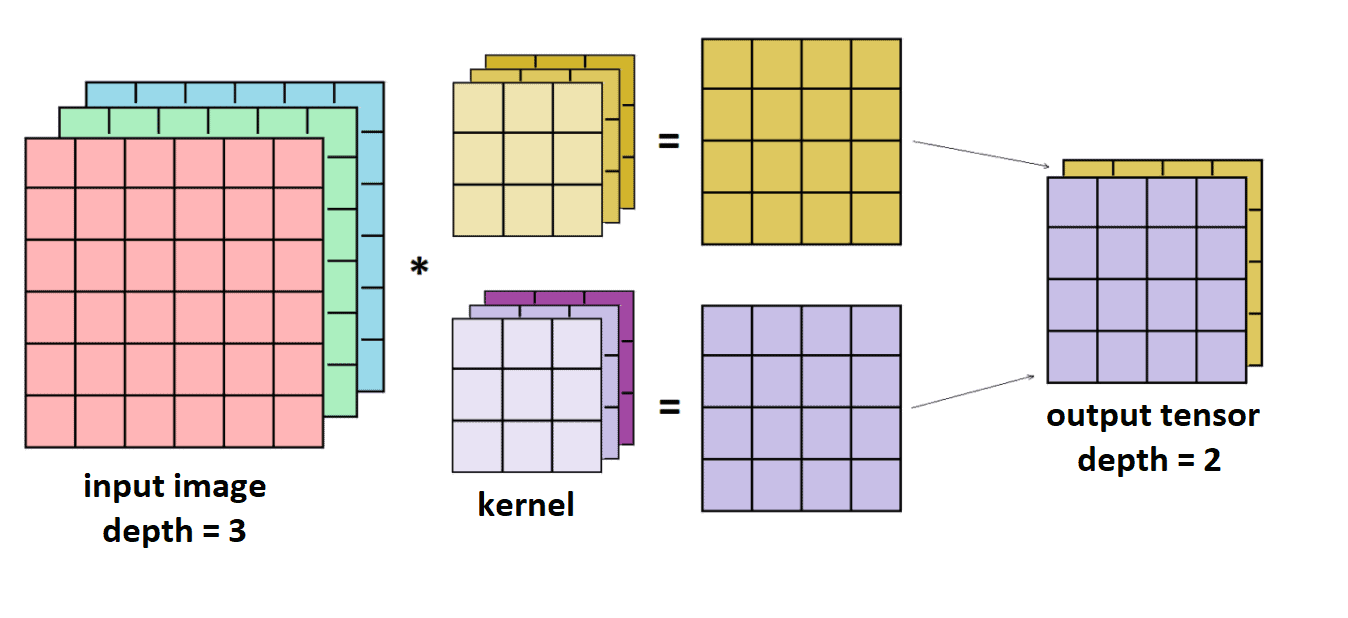
Similarly, if we apply two filters and
, we’ll get two result matrices
and
. After that, we stack together
and
into one tensor
with the dimension
. Analogous to that, if we apply
filters, the output tensor will have dimension
, where
defines depth:
In this short article, we presented the relationship between the term “depth” and CNN’s. Dimensions such as width, height, and depth often sound confusing for beginners, and because of that, we provided a simple example with illustrations.