What Does mdev Mean in ping Statistics?

1. Overview

The ping command is one of the most frequently used commands for testing and troubleshooting network connectivity. Besides giving information about the reachability of a target computer, it also displays several statistics. One of them is mdev, whose meaning isn’t very intuitive.

In this tutorial, we’ll discuss what mdev is and the mathematics behind it. We’ll learn about the effects and reasons of having a high mdev. Finally, we’ll calculate our own mdev using the round-trip times in ping statistics and compare it with the mdev calculated by ping.

2. Meaning of mdev

We’ll briefly discuss the mathematical meaning of mdev in this section.

2.1. ping Statistics

First, let’s inspect the output of ping:

$ ping -c 1 172.66.40.248
PING 172.66.40.248 (172.66.40.248) 56(84) bytes of data.
64 bytes from 172.66.40.248: icmp_seq=1 ttl=128 time=6.08 ms

--- 172.66.40.248 ping statistics ---
1 packets transmitted, 1 received, 0% packet loss, time 0ms
rtt min/avg/max/mdev = 6.082/6.082/6.082/0.000 ms

We sent one ICMP Echo Request message to the host with IP address 172.66.40.248. Consequently, we received the ICMP Echo Reply message successfully.

ping statistics are displayed in the last two lines of the output. The first line shows the number of sent and received messages, packet loss in percent, and the total time.

The last line displays the minimum, average, and maximum of the round-trip times. In addition, it also displays mdev.

What is this mdev? It’s the standard deviation. It measures the dispersion of a data set around the mean of the data set. The data set consists of round-trip times in our case.

There are two definitions of standard deviation.

2.2. Population Standard Deviation

Population standard deviation is one of the two definitions:

According to the definition, the population standard deviation is the square root of the average of the squared deviations from the mean. Here, µ is the mean of the data set, x_i is the value of each data point in the data set, and N is the number of data points in the data set. σ is the population standard deviation.

The higher it is, the more variable are the data points, meaning the data points are spread out over a wider range around the mean.

2.3. Sample Standard Deviation

Sample standard deviation is the other definition:

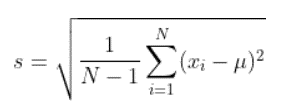
We divide the sum of the squared deviations with N – 1 instead of N.

If the number of data points, N, isn’t large enough, then using the sample standard deviation instead of the population standard deviation gives a more accurate calculation of the spread around the mean. Because of this reason, sample standard deviation is sometimes called the corrected sample standard deviation while population standard deviation is called the uncorrected standard deviation.

It’s clear that as the number of data points becomes larger, the difference between the two standard deviations diminishes.

The Linux operating system uses the population standard deviation for calculating ping statistics. However, there are Unix-based operating systems, like Solaris, that use the sample standard deviation.

2.4. Effect of High Standard Deviation

Having a high standard deviation of round-trip times isn’t desirable. The variation is also known as jitter. High jitter may lead to poor user experience, especially in real-time applications such as streaming audio and video.

There may be many reasons for high jitter. Congestion in a network, malfunctioning hardware, and changes in network routes are some of the reasons.

3. Calculation of mdev

In this section, we’ll calculate the standard deviation of round-trip times using the round-trip times in ping output.

We’ll use two scripts, a Python script and a Bash script, for calculations.

3.1. Python Script

We’ll use the following Python script, calculate_mdev.py, for calculating standard deviation:

#!/usr/bin/python3

import sys
import numpy as np

rtt_list = list(map(float, sys.argv[1:]))

print("\nstandard deviation calculated by NumPy: %.3f ms" % np.std(rtt_list))

This script calculates standard deviation using the NumPy package. It’s a fundamental package for scientific calculation with Python. We import it using import numpy as np.

The script expects the round-trip times as parameters. We get the round-trip times passed to the Python script from the command line using sys.argv[1:]. That’s why we import the sys module using import sys. The first argument, sys.argv[0], is the name of the script. Therefore, we exclude it and get all the other arguments.

Since the arguments read by the script are of type string, we convert the arguments to a list of float values using list(map(float, sys.argv[1:])). We name the list as rtt_list.

Finally, we calculate the standard deviation of the round-trip times by passing rtt_list to the std() function of the NumPy package. We print the output of np.std(rtt_list) using print().

The std() function of the NumPy package uses the population standard deviation.

This script will be called from the Bash script discussed in the next section.

3.2. Bash Script

Here’s the content of the Bash script, mdev.sh:

#!/bin/bash

host=$1
count=$2

ping -c $count $host 2>&1 | tee ./out.ping

./calculate_mdev.py `grep icmp_seq out.ping | awk '{print $7}' | awk -F= awk '{print $7}'`

The script expects two parameters. The first one is the name or IP address of the host we’ll ping. We assign it to the host variable. The second parameter is the number of packets we’ll send to the host. We assign it to the count variable.

Then, we ping $host $count times using the ping -c $count $host 2>&1 | tee ./out.ping command. We direct the output of ping to the file out.ping. We also follow the output of ping in the terminal thanks to the tee command.

Finally, we filter the content of out.ping using grep icmp_seq out.ping | awk ‘{print $7}’ | awk -F= awk ‘{print $7}’. This pipeline just prints the round-trip times, and passes these values to the Python script, calculate_mdev.py, using command substitution.

3.3. Comparison of the Measured and Calculated Values

Let’s run the script for just one ping:

$ ./mdev.sh 172.66.40.248 1
PING 172.66.40.248 (172.66.40.248) 56(84) bytes of data.
64 bytes from 172.66.40.248: icmp_seq=1 ttl=128 time=6.53 ms

--- 172.66.40.248 ping statistics ---
1 packets transmitted, 1 received, 0% packet loss, time 0ms
rtt min/avg/max/mdev = 6.534/6.534/6.534/0.000 ms

standard deviation calculated by NumPy: 0.000 ms

The standard deviation is 0 as expected since there is only one round-trip time.

Now, let’s ping five times:

$ ./mdev.sh 172.66.40.248 5
PING 172.66.40.248 (172.66.40.248) 56(84) bytes of data.
64 bytes from 172.66.40.248: icmp_seq=1 ttl=128 time=5.46 ms
64 bytes from 172.66.40.248: icmp_seq=2 ttl=128 time=5.91 ms
64 bytes from 172.66.40.248: icmp_seq=3 ttl=128 time=5.82 ms
64 bytes from 172.66.40.248: icmp_seq=4 ttl=128 time=6.01 ms
64 bytes from 172.66.40.248: icmp_seq=5 ttl=128 time=5.80 ms

--- 172.66.40.248 ping statistics ---
5 packets transmitted, 5 received, 0% packet loss, time 4007ms
rtt min/avg/max/mdev = 5.469/5.805/6.019/0.190 ms

standard deviation calculated by NumPy: 0.186 ms

The standard deviation in the ping statistics is 0.190 ms. However, the standard deviation calculated by our script is 0.186 ms. ping measures the times in microseconds, but prints the results rounded in milliseconds. We use the rounded round-trip times. That’s the reason for the difference between them.

4. Conclusion

In this article, we discussed the meaning of mdev in the ping statistics. We saw that it’s the standard deviation of round-trip times.

Firstly, we learned what standard deviation is. We saw that it’s the amount of dispersion of data points around the mean. There are two definitions of standard deviation. One of them is the population or uncorrected standard deviation. The other one is the sample or corrected standard deviation. We learned that the implementation of ping in Linux uses the first definition.

Later, we briefly discussed the effects of a high standard deviation of round-trip times, known as jitter.

Finally, we calculated the standard deviation of measured round-trip times using the std() function of Python’s NumPy package. Because of the rounded round-trip times we used, there was a slight difference between the standard deviation we calculated and the one in ping statistics.