1. Introduction
In this tutorial, we’re going to take a look at Prim’s algorithm. We’ll see what it is and how to implement it in Kotlin.
2. What Is Prim’s Algorithm?
Prim’s Algorithm is a greedy algorithm that finds a minimum spanning tree for a weighted undirected graph. But what does that mean?
An undirected graph is one where the edges have no direction. That is, we can traverse any edge in either direction. Being weighted then means that every edge has a cost, or weight, associated with it:
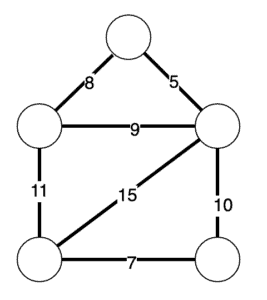
A spanning tree is then a subset of edges within our graph so that all of our nodes are connected. If we have a weighted graph, our spanning tree has a weight equivalent to the sum of all the used edges. Given that, a minimum spanning tree is simply the spanning tree with the lowest possible weight:
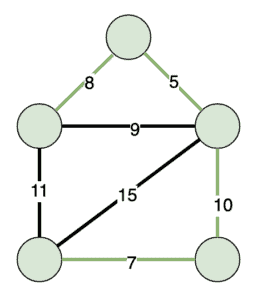
Prim’s Algorithm allows us to find such a minimum spanning tree within our graph.
To achieve this, we start by marking any one node in our graph as visited and leaving all of the others as unvisited:
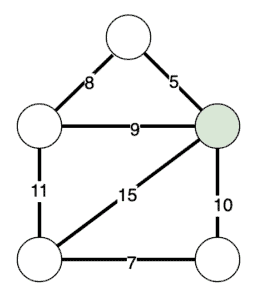
The algorithm is then:
- Find the edge between a visited and unvisited node with the lowest weight.
- Add this edge to our spanning tree.
- Mark the new node as visited.
- Suppose there are any nodes that we haven’t visited, then repeat. Once we’ve seen every node, then we’re finished.
This will then iteratively find our minimum spanning tree:
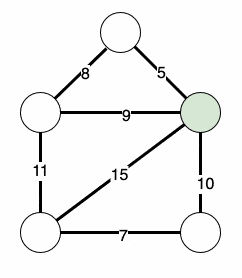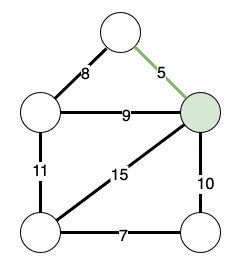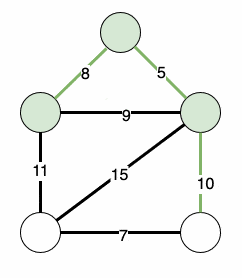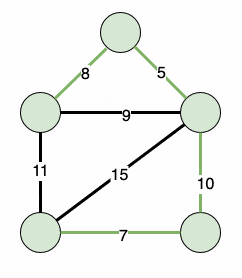
3. Implementing Prim’s Algorithm
Now that we’ve seen Prim’s algorithm, let’s look at how to implement it in Kotlin.
3.1. Representing the Graph
The first thing we need to be able to do is represent our graph. This means some collection of edges, where each edge consists of the two nodes it connects and the weight of that edge.
For this article’s sake, we’ll represent our nodes as strings. These can be considered just the ID of the node. In reality, we might want to use a richer type instead. The only important thing is identifying that two nodes are identical.
Our Edge can then be a data class with these two strings and a value for the weight:
data class Edge(
val first: String,
val second: String,
val weight: Int
)
Now, we need the Graph itself. This is just a collection of edges since the edges can then give us our nodes:
data class Graph(val edges: Collection<Edge>)
This does mean that we can’t represent any disconnected nodes – that is, nodes for which there are zero edges – but they can’t be part of a spanning tree anyway.
We’ll also add a couple of helper methods to the Graph class. The first is one to give us a collection of all the nodes in the graph:
fun getNodes() : Collection<String> {
return edges.flatMap { setOf(it.first, it.second) }.distinct()
}
The second will provide us with all of the edges that are attached to a given node:
fun getEdgesForNode(node: String) : Collection<Edge> {
return edges.filter { it.first == node || it.second == node }
}
3.2. Preparing the Algorithm
Now that we have a graph representation, we can implement our algorithm. We’ll do this as a free function that takes, as input, a graph and returns another graph with only the edges from our minimum spanning tree:
fun prims(graph: Graph) : Graph {
// Algorithm goes here.
}
The first thing that we need is a couple of collections – one for the collection of nodes that we’ve already visited and one for the collection of edges that we’re going to include in our result:
val visitedNodes = mutableSetOf<String>()
val edges = mutableSetOf<Edge>()
We also need to pick a starting node. This can be any node in the graph, so we’ll grab a random one and add it to our set of visited nodes:
visitedNodes.add(graph.getNodes().random())
We could have equally well used the first one returned, the one with the most edges, or any other method we wished.
3.3. Selecting the Edges
Now that we’ve got our starting conditions, we’re ready to select the edges. This is the actual core of the algorithm.
At each iteration, we need to select the edge that goes from a visited node to an unvisited node and has the minimum weight. Let’s break that down a bit.
The first thing we need is all the edges that come from a visited node. We can do this by mapping our collection of visited nodes to the edges for that node, using the helper function that we wrote earlier:
val allEdges = visitedNodes.flatMap { graph.getEdgesForNode(it) }
Next, we need to filter these to include only the ones that go to an unvisited node. Note that we don’t know which of the two nodes for this edge is which, but we also don’t need to care. It’s a guarantee that at least one of them is a visited node – or else we wouldn’t be looking at it – so we need to see if one of them is an unvisited node:
val unvisitedEdges = allEdges.filter { !visitedNodes.contains(it.first) || !visitedNodes.contains(it.second) }
Now that we have this collection of edges, we need to find the one with the lowest weight. This is simply sorting the collection by weight and taking the first in the list. However, Kotlin gives us the minBy function that will do this for us as a single step:
val nextEdge = unvisitedEdges.minBy { it.weight }
At this point, we can mark the nodes as visited and add this edge to our results. Again, we don’t know whether the first or second node for the edge is our unvisited one, but that doesn’t matter. Because we’re storing our visited nodes in a Set, we can just add both of them and trust the Set to do the right thing:
visitedNodes.addAll(setOf(nextEdge.first, nextEdge.second))
edges.add(nextEdge)
Now, all we need to do is repeat this until we’ve visited every node:
while (!visitedNodes.containsAll(graph.getNodes())) {
val nextEdge = visitedNodes.flatMap { graph.getEdgesForNode(it) }
.filter { !visitedNodes.contains(it.first) || !visitedNodes.contains(it.second) }
.minBy { it.weight }
visitedNodes.addAll(setOf(nextEdge.first, nextEdge.second))
edges.add(nextEdge)
}
4. Testing the Algorithm
Now that we’ve got our algorithm, let’s ensure it works. We’ll start with our example graph from earlier, only we’ve now labeled the nodes:
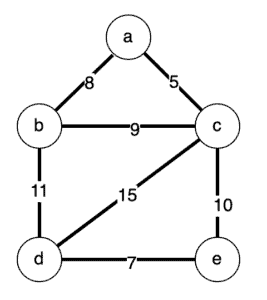
We can represent this with our Graph class as:
val graph = Graph(setOf(
Edge(first = "a", second = "b", weight = 8),
Edge(first = "a", second = "c", weight = 5),
Edge(first = "b", second = "c", weight = 9),
Edge(first = "b", second = "d", weight = 11),
Edge(first = "c", second = "d", weight = 15),
Edge(first = "c", second = "e", weight = 10),
Edge(first = "d", second = "e", weight = 7)
))
If we then call our function on this and output the results, we’ll see:
Graph(edges=[
Edge(first=a, second=c, weight=5),
Edge(first=a, second=b, weight=8),
Edge(first=c, second=e, weight=10),
Edge(first=d, second=e, weight=7)
])
So, our algorithm has picked the same four edges we saw earlier.
5. Disjoint Graphs
What happens if we try to use this on a disjoint graph? That is, a graph where there are nodes that aren’t all connected:
Let’s try it out:
val graph = Graph(setOf(
Edge(first = "a", second = "b", weight = 2),
Edge(first = "c", second = "d", weight = 3),
))
prims(graph)
When we run this, rather than getting a new Graph returned with our minimum spanning tree, we instead get a NoSuchElementException thrown. This occurs because the algorithm reaches a point where there are unvisited nodes, but no edges connect from a visited node to an unvisited one. As such, finding a spanning tree for this graph is impossible.
6. Summary
In this article, we’ve looked at Prim’s algorithm, both in terms of what it is and how we can break it down and implement it in Kotlin. Why not try it out for yourself next time you need to work with spanning trees?
As always, all of the code for this article is available over on GitHub.
