Let's get started with a Microservice Architecture with Spring Cloud:
Check if Two Strings Are Rotations of Each Other
Last updated: March 26, 2025
1. Overview
In this tutorial, we’ll learn how to check if a string is a rotation of another string.
We’ll briefly discuss what string rotation is. Then, we’ll look at some algorithms to solve the problem with code insight and complexity analysis.
2. Introduction to String Rotation
Before digging into some solutions, let’s discuss string rotation and what we should test for the algorithm.
2.1. String and String Rotation
A string is a sequence of primitive characters, and in Java, it’s wrapped in a String class. Although two strings might be different objects, we can compare their internal characters and check, for example, whether they’re equal or contain common patterns.
A rotation of a string is a string that contains the same characters but in a different order. Specifically, one or more characters are shifted from the original position. For example, the string “cdab” is a rotation of “abcd”. This can be seen in two steps:
- abcd -> dabc shifts the last d to the first position
- dabc -> cdab shifts the last c to the first position
This is done by shifting from the right, but it could be done also from the left.
Notably, we can say that if two strings aren’t the same length, they can’t be one rotation of the other.
2.2. Variable Names
To demonstrate, we’ll always refer to the rotation as the potential string candidate to check whether it’s an actual rotation of an origin.
2.3. Unit Testing
We have only two cases to test whether a string is a rotation. Notably, a string is a rotation of itself. Therefore, we might also want to test that corner case.
3. Rotation Contained in Doubled String
We can naively think that if we double our origin string, at some point, it will contain a rotation. We can picture this intuitively:
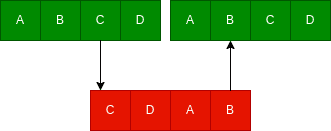
3.1. Algorithm
The algorithm is straightforward:
boolean doubledOriginContainsRotation(String origin, String rotation) {
if (origin.length() == rotation.length()) {
return origin.concat(origin)
.contains(rotation);
}
return false;
}3.2. Code Insight
We concatenate the origin with itself, and we check if it contains the potential rotation:
return origin.concat(origin).contains(rotation);Let’s look at the algorithm complexity:
- Time Complexity: O(n*m) where n is the length of the concatenation and m is the length of the rotation
- Space Complexity: O(n) proportional to the length of the strings
3.3. Unit Tests
Let’s test the rotation contained in the doubled origin string when the rotation is ok. We’ll also test when the origin is the exact string as the rotation:
@Test
void givenDoubledOrigin_whenCheckIfOriginContainsRotation_thenIsRotation() {
assertTrue(doubledOriginContainsRotation("abcd", "cdab"));
assertTrue(doubledOriginContainsRotation("abcd", "abcd"));
}Let’s test when the rotation isn’t contained. We’ll also test when the rotation is a longer string than the origin:
@Test
void givenDoubledOrigin_whenCheckIfOriginContainsRotation_thenNoRotation() {
assertFalse(doubledOriginContainsRotation("abcd", "bbbb"));
assertFalse(doubledOriginContainsRotation("abcd", "abcde"));
}4. Rotation From Common Start With Origin
We can use the previous approach and build a more detailed algorithm.
First, let’s collect all the indexes in the rotation of the starting character of the origin. Finally, we loop over the origin and compare the strings at shifted positions. Let’s picture these steps in more detail:
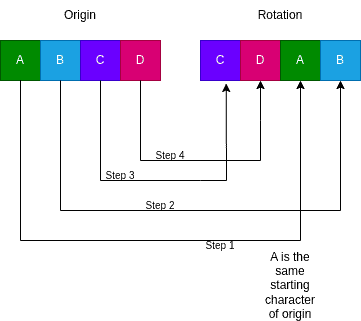
4.1. Algorithm
Once we know the common characters, we can check whether the strings continue to be equal:
boolean isRotationUsingCommonStartWithOrigin(String origin, String rotation) {
if (origin.length() == rotation.length()) {
List<Integer> indexes = IntStream.range(0, origin.length())
.filter(i -> rotation.charAt(i) == origin.charAt(0))
.boxed()
.collect(Collectors.toList());
for (int startingAt : indexes) {
if (isRotation(startingAt, rotation, origin)) {
return true;
}
}
}
return false;
}
boolean isRotation(int startingAt, String rotation, String origin) {
for (int i = 0; i < origin.length(); i++) {
if (rotation.charAt((startingAt + i) % origin.length()) != origin.charAt(i)) {
return false;
}
}
return true;
}4.2. Code Insight
There are two main points to focus on. The first is where we collect the indexes:
List<Integer> indexes = IntStream.range(0, origin.length())
.filter(i -> rotation.charAt(i) == origin.charAt(0))
.boxed()
.collect(Collectors.toList());These are the positions in the rotation where we can find the starting character of the origin.
Then, we loop over the strings and check at shifted positions:
for (int i = 0; i < origin.length(); i++) {
if (rotation.charAt((startingAt + i) % origin.length()) != origin.charAt(i)) {
return false;
}
}Notably, we use the modulo (%) to return from the first index when we exceed the rotation length.
Let’s look at the algorithm complexity:
- Time Complexity: O(n*m) where n is the length of the origin and m is the number of indexes found
- Space Complexity: O(n)
4.3. Unit Tests
Let’s test when the rotation has common starting characters with the origin and the remaining part of the strings are equal:
@Test
void givenOriginAndRotationInput_whenCheckingCommonStartWithOrigin_thenIsRotation() {
assertTrue(isRotationUsingCommonStartWithOrigin("abcd", "cdab"));
assertTrue(isRotationUsingCommonStartWithOrigin("abcd", "abcd"));
}Let’s test when the rotation has common starting characters, but it’s either too long, or the remaining part doesn’t match:
@Test
void givenOriginAndRotationInput_whenCheckingCommonStartWithOrigin_thenNoRotation() {
assertFalse(isRotationUsingCommonStartWithOrigin("abcd", "bbbb"));
assertFalse(isRotationUsingCommonStartWithOrigin("abcd", "abcde"));
}5. Rotation Comparing Prefix and Suffix
If we find a common starting character of origin and rotation, we can also say that our strings will be equal before and after that matching point. For example, our origin string “abcd” has the common c at position 2 with “cdab”. However, prefixes and suffixes will need to be equal accordingly for the remaining portion of the strings:
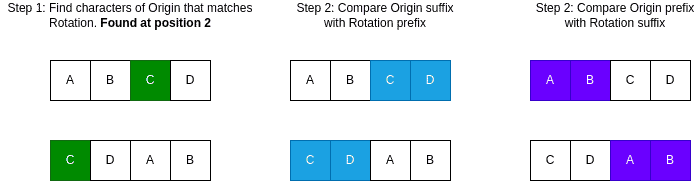
5.1. Algorithm
Whenever we find a common character, we can then compare the prefix and suffix for those segments of characters remaining, inverting the origin and the rotation:
boolean isRotationUsingSuffixAndPrefix(String origin, String rotation) {
if (origin.length() == rotation.length()) {
return checkPrefixAndSuffix(origin, rotation);
}
return false;
}
boolean checkPrefixAndSuffix(String origin, String rotation) {
if (origin.length() == rotation.length()) {
for (int i = 0; i < origin.length(); i++) {
if (origin.charAt(i) == rotation.charAt(0)) {
if (checkRotationPrefixWithOriginSuffix(origin, rotation, i)) {
if (checkOriginPrefixWithRotationSuffix(origin, rotation, i)) {
return true;
}
}
}
}
}
return false;
}
boolean checkRotationPrefixWithOriginSuffix(String origin, String rotation, int i) {
return origin.substring(i)
.equals(rotation.substring(0, origin.length() - i));
}
boolean checkOriginPrefixWithRotationSuffix(String origin, String rotation, int i) {
return origin.substring(0, i)
.equals(rotation.substring(origin.length() - i));
}
5.2. Code Insight
We have two checks to make. First, we compare the rotation prefix with the origin suffix:
return origin.substring(i)
.equals(rotation.substring(0, origin.length() - i));Then, we compare the rotation suffix with the origin prefix:
return origin.substring(0, i)
.equals(rotation.substring(origin.length() - i));Notably, these checks can be done in any order.
Let’s look at the algorithm complexity:
- Time Complexity: O(n*n) comparing two strings of length n
- Space Complexity: O(n)
5.3. Unit Tests
Let’s test when the rotation has equal suffix and prefix with the origin given a common character:
@Test
void givenOriginAndRotationInput_whenCheckingUsingSuffixAndPrefix_thenIsRotation() {
assertTrue(isRotationUsingSuffixAndPrefix("abcd", "cdab"));
assertTrue(isRotationUsingSuffixAndPrefix("abcd", "abcd"));
}Let’s test when the rotation doesn’t have an equal suffix and prefix with the origin:
@Test
void givenOriginAndRotationInput_whenCheckingUsingSuffixAndPrefix_thenNoRotation() {
assertFalse(isRotationUsingSuffixAndPrefix("abcd", "bbbb"));
assertFalse(isRotationUsingSuffixAndPrefix("abcd", "abcde"));
}6. Rotation Comparing Queue of Characters
Another view of the problem is imagining the two strings as queues. Then, we shift the top character of the rotation into the tail and compare the new queue with the origin. Let’s see a simple picture of the queues:
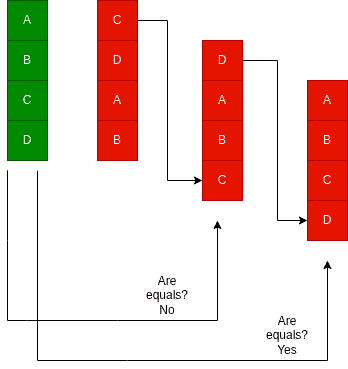
6.1. Algorithm
We create the two queues. Then, we shift from the top character to the bottom of the rotation while checking if it’s equal to the origin at every step.
boolean isRotationUsingQueue(String origin, String rotation) {
if (origin.length() == rotation.length()) {
return checkWithQueue(origin, rotation);
}
return false;
}
boolean checkWithQueue(String origin, String rotation) {
if (origin.length() == rotation.length()) {
Queue<Character> originQueue = getCharactersQueue(origin);
Queue<Character> rotationQueue = getCharactersQueue(rotation);
int k = rotation.length();
while (k > 0 && null != rotationQueue.peek()) {
k--;
char ch = rotationQueue.peek();
rotationQueue.remove();
rotationQueue.add(ch);
if (rotationQueue.equals(originQueue)) {
return true;
}
}
}
return false;
}
Queue<Character> getCharactersQueue(String origin) {
return origin.chars()
.mapToObj(c -> (char) c)
.collect(Collectors.toCollection(LinkedList::new));
}6.2. Code Insight
After creating the queue, what is relevant is how we can assert that our strings are equal:
int k = rotation.length();
while (k > 0 && null != rotationQueue.peek()) {
k--;
char ch = rotationQueue.peek();
rotationQueue.remove();
rotationQueue.add(ch);
if (rotationQueue.equals(originQueue)) {
return true;
}
}Moving the top element of the queue to the bottom in constant time gives us a new shifted object to compare with the origin.
Let’s look at the algorithm complexity:
- Time Complexity: O(n*n) worst-case where we loop over the whole queue while comparing with the origin
- Space Complexity: O(n)
6.3. Unit Tests
Let’s test that using queues when shifting the rotation from the top to the tail will match the origin:
@Test
void givenOriginAndRotationInput_whenCheckingUsingQueues_thenIsRotation() {
assertTrue(isRotationUsingQueue("abcd", "cdab"));
assertTrue(isRotationUsingQueue("abcd", "abcd"));
}Let’s test using queues when they won’t be equal:
@Test
void givenOriginAndRotationInput_whenCheckingUsingQueues_thenNoRotation() {
assertFalse(isRotationUsingQueue("abcd", "bbbb"));
assertFalse(isRotationUsingQueue("abcd", "abcde"));
}7. Conclusion
In this article, we saw some algorithms to check whether a string is a rotation of another string. We saw how to search for common characters and assert equality using a doubled-origin string and the contains() string method. Similarly, we can use algorithms to check whether the remaining parts of the string match at shifted positions or using suffixes and prefixes. Finally, we also saw an example using queues and moving the peek to the tail of the rotation until it’s equal to the origin.
The code backing this article is available on GitHub. Once you're logged in as a Baeldung Pro Member, start learning and coding on the project.

















