Median of Stream of Integers using Heap in Java

1. Overview

In this tutorial, we’ll learn how to compute the median of a stream of integers.

We’ll proceed by stating the problem with examples, then analyze the problem, and finally implement several solutions in Java.

2. Problem Statement

Median is the middle value of an ordered data set. For a set of integers, there are just as many elements less than the median as greater.

In an ordered set of:

• odd number of integers, the middle element is the median – in the ordered set { 5, 7, 10 }, the median is 7
• even number of integers, there’s no middle element; the median is computed as the average of the two middle elements – in the ordered set {5, 7, 8, 10}, the median is (7 + 8) / 2 = 7.5

Now, let’s assume that instead of a finite set, we’re reading integers off a data stream. We can define the median of a stream of integers as the median of the set of integers read so far.

Let’s formalize the problem statement. Given an input of a stream of integers, we must design a class that performs the following two tasks for each integer that we read:

1. Add the integer to the set of integers
2. Find the median of the integers read so far

For example:

add 5         // sorted-set = { 5 }, size = 1
get median -> 5

add 7         // sorted-set = { 5, 7 }, size = 2 
get median -> (5 + 7) / 2 = 6

add 10        // sorted-set = { 5, 7, 10 }, size = 3 
get median -> 7

add 8         // sorted-set = { 5, 7, 8, 10 }, size = 4 
get median -> (7 + 8) / 2 = 7.5
..

Although the stream is non-finite, we can assume that we can hold all the elements of the stream in memory at once.

We can represent our tasks as the following operations in code:

void add(int num);

double getMedian();

3. Naive Approach

3.1. Sorted List

Let’s begin with a simple idea – we can compute the median of a sorted list of integers by accessing the middle element or the middle two elements of the list, by index. The time complexity of the getMedian operation is O(1).

While adding a new integer, we must determine its correct position in the list such that the list remains sorted. This operation can be performed in O(n) time, where n is the size of the list. So, the overall cost of adding a new element to the list and computing the new median is O(n).

3.2. Improving on the Naive Approach

The add operation runs in linear time, which isn’t optimal. Let’s try to address that in this section.

We can split the list into two sorted lists – the smaller half of the integers sorted in decreasing order, and the larger half of the integers in increasing order. We can add a new integer into the appropriate half such that the size of the lists differs by 1, at most:

if element is smaller than min. element of larger half:
    insert into smaller half at appropriate index
    if smaller half is much bigger than larger half:
        remove max. element of smaller half and insert at the beginning of larger half (rebalance)
else
    insert into larger half at appropriate index:
    if larger half is much bigger than smaller half:
        remove min. element of larger half and insert at the beginning of smaller half (rebalance)

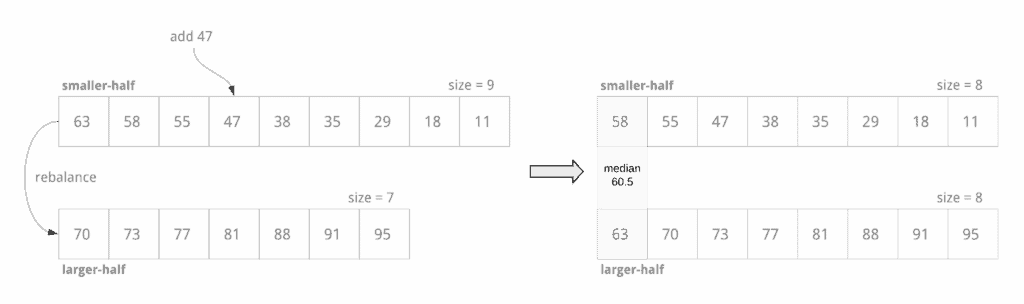
Now, we can compute the median:

if lists contain equal number of elements:
    median = (max. element of smaller half + min. element of larger half) / 2
else if smaller half contains more elements:
    median = max. element of smaller half
else if larger half contains more elements:
    median = min. element of larger half

Though we have only improved the time complexity of the add operation by some constant factor, we have made progress.

Let’s analyze the elements we access in the two sorted lists. We potentially access each element as we shift them during the (sorted) add operation. More importantly, we access the minimum and maximum (extremums) of the larger and smaller halves respectively, during the add operation for rebalancing and during the getMedian operation.

We can see that extremums are the first elements of their respective lists. So, we must optimize for accessing the element at index 0 for each half to improve the overall running time of the add operation.

4. Heap-based Approach

Let’s refine our understanding of the problem, by applying what we’ve learned from our naive approach:

1. We must get the minimum/maximum element of a dataset in O(1) time
2. The elements don’t have to be kept in a sorted order as long as we can get the minimum/maximum element efficiently
3. We need to find an approach for adding an element to our dataset that costs less than O(n) time

Next, we’ll look at the Heap data structure that helps us achieve our goals efficiently.

4.1. Heap Data Structure

Heap is a data structure that is usually implemented with an array but can be thought of as a binary tree.

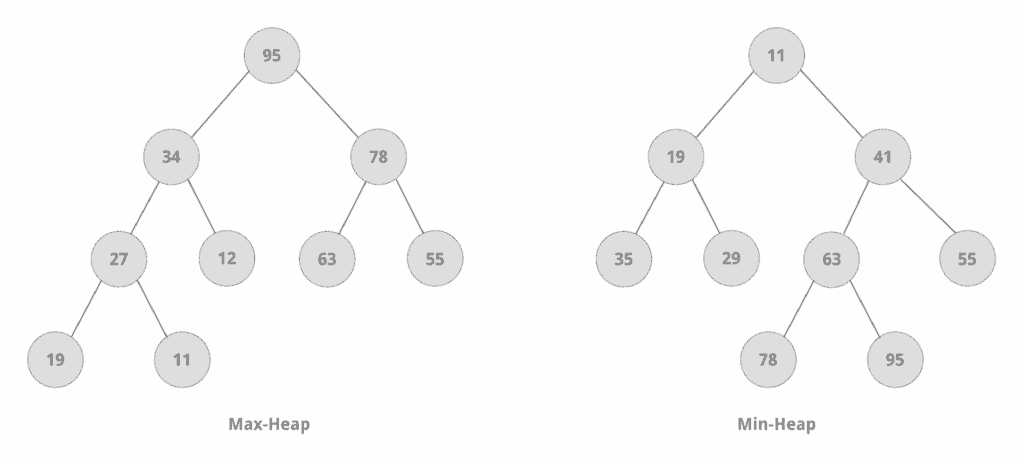
Heaps are constrained by the heap property:

4.1.1. Max–heap Property

A (child) node can’t have a value greater than that of its parent. Hence, in a max-heap, the root node always has the largest value.

4.1.2. Min–heap Property

A (parent) node can’t have a value greater than that of its children. Thus, in a min-heap, the root node always has the smallest value.

In Java, the PriorityQueue class represents a heap. Let’s move ahead to our first solution using heaps.

4.2. First Solution

Let’s replace the lists in our naive approach with two heaps:

• A min-heap that contains the larger half of the elements, with the minimum element at the root
• A max-heap that contains the smaller half of the elements, with the maximum element at the root

Now, we can add the incoming integer to the relevant half by comparing it with the root of the min-heap. Next, if after insertion, the size of one heap differs from that of the other heap by more than 1, we can rebalance the heaps, thus maintaining a size difference of at most 1:

if size(minHeap) > size(maxHeap) + 1:
    remove root element of minHeap, insert into maxHeap
if size(maxHeap) > size(minHeap) + 1:
    remove root element of maxHeap, insert into minHeap

With this approach, we can compute the median as the average of the root elements of both the heaps, if the size of the two heaps is equal. Otherwise, the root element of the heap with more elements is the median.

We’ll use the PriorityQueue class to represent the heaps. The default heap property of a PriorityQueue is min-heap. We can create a max-heap by using a Comparator.reverserOrder that uses the reverse of the natural order:

class MedianOfIntegerStream {

    private Queue<Integer> minHeap, maxHeap;

    MedianOfIntegerStream() {
        minHeap = new PriorityQueue<>();
        maxHeap = new PriorityQueue<>(Comparator.reverseOrder());
    }

    void add(int num) {
        if (!minHeap.isEmpty() && num < minHeap.peek()) {
            maxHeap.offer(num);
            if (maxHeap.size() > minHeap.size() + 1) {
                minHeap.offer(maxHeap.poll());
            }
        } else {
            minHeap.offer(num);
            if (minHeap.size() > maxHeap.size() + 1) {
                maxHeap.offer(minHeap.poll());
            }
        }
    }

    double getMedian() {
        double median;
        if (minHeap.size() < maxHeap.size()) {
            median = maxHeap.peek();
        } else if (minHeap.size() > maxHeap.size()) {
            median = minHeap.peek();
        } else {
            median = (minHeap.peek() + maxHeap.peek()) / 2.0; 
        }
        return median;
    }
}

Before we analyze the running time of our code, let’s look at the time complexity of the heap operations we have used:

find-min/find-max        O(1)    

delete-min/delete-max    O(log n)

insert                   O(log n)

So, the getMedian operation can be performed in O(1) time as it requires the find-min and find-max functions only. The time complexity of the add operation is O(log n) – three insert/delete calls each requiring O(log n) time.

4.3. Heap Size Invariant Solution

In our previous approach, we compared each new element with the root elements of the heaps. Let’s explore another approach using heap in which we can leverage the heap property to add a new element in the appropriate half.

As we have done for our previous solution, we begin with two heaps – a min-heap and a max-heap. Next, let’s introduce a condition: the size of the max-heap must be (n / 2) at all times, while the size of the min-heap can be either (n / 2) or (n / 2) + 1, depending on the total number of elements in the two heaps. In other words, we can allow only the min-heap to have an extra element, when the total number of elements is odd.

With our heap size invariant, we can compute the median as the average of the root elements of both heaps, if the sizes of both heaps are (n / 2). Otherwise, the root element of the min-heap is the median.

When we add a new integer, we have two scenarios:

1. Total no. of existing elements is even
   size(min-heap) == size(max-heap) == (n / 2)

2. Total no. of existing elements is odd
   size(max-heap) == (n / 2)
   size(min-heap) == (n / 2) + 1

We can maintain the invariant by adding the new element to one of the heaps and rebalancing every time:

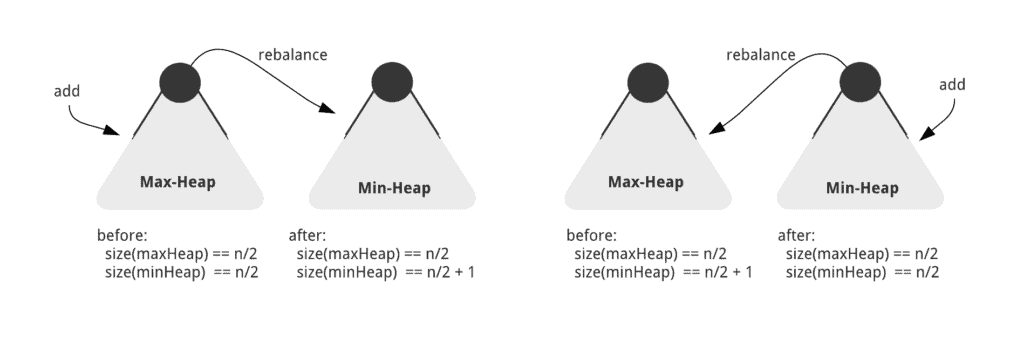
The rebalancing works by moving the largest element from the max-heap to the min-heap, or by moving the smallest element from the min-heap to the max-heap. This way, though we’re not comparing the new integer before adding it to a heap, the subsequent rebalancing ensures that we honor the underlying invariant of smaller and larger halves.

Let’s implement our solution in Java using PriorityQueues:

class MedianOfIntegerStream {

    private Queue<Integer> minHeap, maxHeap;

    MedianOfIntegerStream() {
        minHeap = new PriorityQueue<>();
        maxHeap = new PriorityQueue<>(Comparator.reverseOrder());
    }

    void add(int num) {
        if (minHeap.size() == maxHeap.size()) {
            maxHeap.offer(num);
            minHeap.offer(maxHeap.poll());
        } else {
            minHeap.offer(num);
            maxHeap.offer(minHeap.poll());
        }
    }

    double getMedian() {
        double median;
        if (minHeap.size() > maxHeap.size()) {
            median = minHeap.peek();
        } else {
            median = (minHeap.peek() + maxHeap.peek()) / 2.0;
        }
        return median;
    }
}

The time complexities of our operations remain unchanged: getMedian costs O(1) time, while add runs in time O(log n) with exactly the same number of operations.

Both the heap-based solutions offer similar space and time complexities. While the second solution is clever and has a cleaner implementation, the approach isn’t intuitive. On the other hand, the first solution follows our intuition naturally, and it’s easier to reason about the correctness of its add operation.

5. Conclusion

In this tutorial, we learned how to compute the median of a stream of integers. We evaluated a few approaches and implemented a couple of different solutions in Java using PriorityQueue.