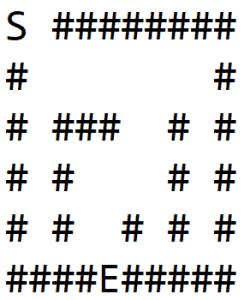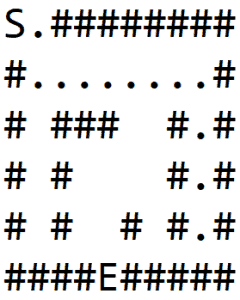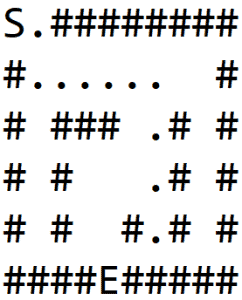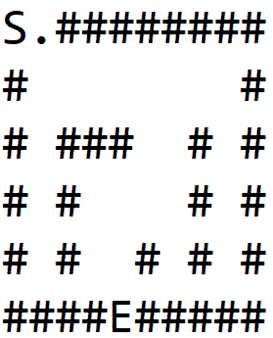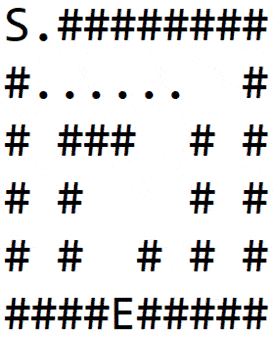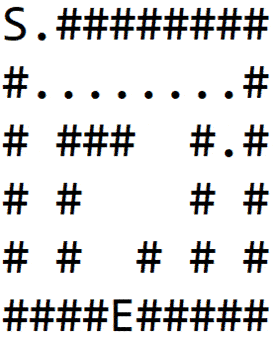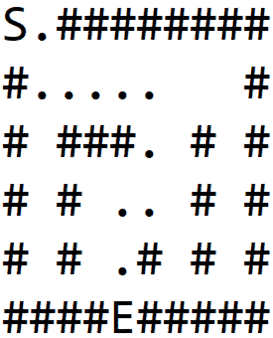A Maze Solver in Java

1. Introduction

In this article, we’ll explore possible ways to navigate a maze, using Java.

Consider the maze to be a black and white image, with black pixels representing walls, and white pixels representing a path. Two white pixels are special, one being the entry to the maze and another exit.

Given such a maze, we want to find a path from entry to the exit.

2. Modelling the Maze

We’ll consider the maze to be a 2D integer array. Meaning of numerical values in the array will be as per the following convention:

• 0 -> Road
• 1 -> Wall
• 2 -> Maze entry
• 3 -> Maze exit
• 4 -> Cell part of the path from entry to exit

We’ll model the maze as a graph. Entry and exit are the two special nodes, between which path is to be determined.

A typical graph has two properties, nodes, and edges. An edge determines the connectivity of graph and links one node to another.

Hence we’ll assume four implicit edges from each node, linking the given node to its left, right, top and bottom node.

Let’s define the method signature:

public List<Coordinate> solve(Maze maze) {
}

The input to the method is a maze, which contains the 2D array, with naming convention defined above.

The response of the method is a list of nodes, which forms a path from the entry node to the exit node.

3. Recursive Backtracker (DFS)

3.1. Algorithm

One fairly obvious approach is to explore all possible paths, which will ultimately find a path if it exists. But such an approach will have exponential complexity and will not scale well.

However, it’s possible to customize the brute force solution mentioned above, by backtracking and marking visited nodes, to obtain a path in a reasonable time. This algorithm is also known as Depth-first search.

This algorithm can be outlined as:

1. If we’re at the wall or an already visited node, return failure
2. Else if we’re the exit node, then return success
3. Else, add the node in path list and recursively travel in all four directions. If failure is returned, remove the node from the path and return failure. Path list will contain a unique path when exit is found

Let’s apply this algorithm to the maze shown in Figure-1(a), where S is the starting point, and E is the exit.

For each node, we traverse each direction in order: right, bottom, left, top.

In 1(b), we explore a path and hit the wall. Then we backtrack till a node is found which has non-wall neighbors, and explore another path as shown in 1(c).

We again hit the wall and repeat the process to finally find the exit, as shown in 1(d):

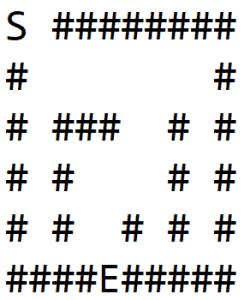
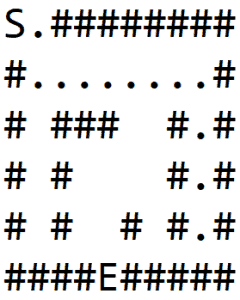
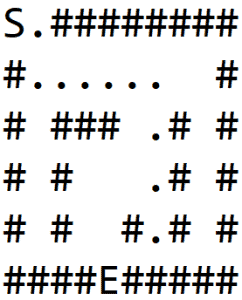
3.2. Implementation

Let’s now see the Java implementation:

First, we need to define the four directions. We can define this in terms of coordinates. These coordinates, when added to any given coordinate, will return one of the neighboring coordinates:

private static int[][] DIRECTIONS 
  = { { 0, 1 }, { 1, 0 }, { 0, -1 }, { -1, 0 } };

We also need a utility method which will add two coordinates:

private Coordinate getNextCoordinate(
  int row, int col, int i, int j) {
    return new Coordinate(row + i, col + j);
}

We can now define the method signature solve. The logic here is simple – if there is a path from entry to exit, then return the path, else, return an empty list:

public List<Coordinate> solve(Maze maze) {
    List<Coordinate> path = new ArrayList<>();
    if (
      explore(
        maze, 
        maze.getEntry().getX(),
        maze.getEntry().getY(),
        path
      )
      ) {
        return path;
    }
    return Collections.emptyList();
}

Let’s define the explore method referenced above. If there’s a path then return true, with the list of coordinates in the argument path. This method has three main blocks.

First, we discard invalid nodes i.e. the nodes which are outside the maze or are part of the wall. After that, we mark the current node as visited so that we don’t visit the same node again and again.

Finally, we recursively move in all directions if the exit is not found:

private boolean explore(
  Maze maze, int row, int col, List<Coordinate> path) {
    if (
      !maze.isValidLocation(row, col) 
      || maze.isWall(row, col) 
      || maze.isExplored(row, col)
    ) {
        return false;
    }

    path.add(new Coordinate(row, col));
    maze.setVisited(row, col, true);

    if (maze.isExit(row, col)) {
        return true;
    }

    for (int[] direction : DIRECTIONS) {
        Coordinate coordinate = getNextCoordinate(
          row, col, direction[0], direction[1]);
        if (
          explore(
            maze, 
            coordinate.getX(), 
            coordinate.getY(), 
            path
          )
        ) {
            return true;
        }
    }

    path.remove(path.size() - 1);
    return false;
}

This solution uses stack size up to the size of the maze.

4. Variant – Shortest Path (BFS)

4.1. Algorithm

The recursive algorithm described above finds the path, but it isn’t necessarily the shortest path. To find the shortest path, we can use another graph traversal approach known as Breadth-first search.

In DFS, one child and all its grandchildren were explored first, before moving on to another child. Whereas in BFS, we’ll explore all the immediate children before moving on to the grandchildren. This will ensure that all nodes at a particular distance from the parent node, are explored at the same time.

The algorithm can be outlined as follows:

1. Add the starting node in queue
2. While the queue is not empty, pop a node, do following:
   1. If we reach the wall or the node is already visited, skip to next iteration
   2. If exit node is reached, backtrack from current node till start node to find the shortest path
   3. Else, add all immediate neighbors in the four directions in queue

One important thing here is that the nodes must keep track of their parent, i.e. from where they were added to the queue. This is important to find the path once exit node is encountered.

Following animation shows all the steps when exploring a maze using this algorithm. We can observe that all the nodes at same distance are explored first before moving onto the next level:

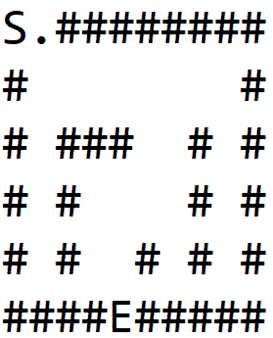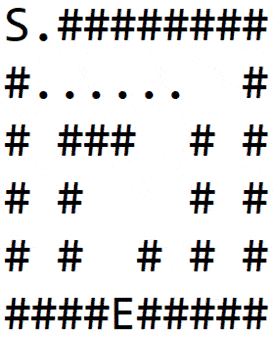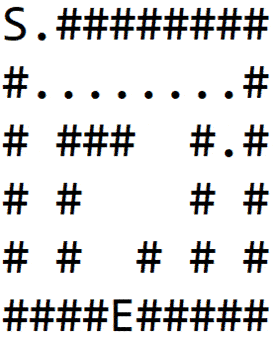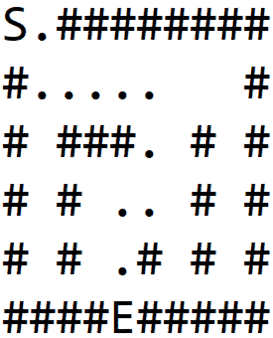
4.2. Implementation

Lets now implement this algorithm in Java. We will reuse the DIRECTIONS variable defined in previous section.

Lets first define a utility method to backtrack from a given node to its root. This will be used to trace the path once exit is found:

private List<Coordinate> backtrackPath(
  Coordinate cur) {
    List<Coordinate> path = new ArrayList<>();
    Coordinate iter = cur;

    while (iter != null) {
        path.add(iter);
        iter = iter.parent;
    }

    return path;
}

Let’s now define the core method solve. We’ll reuse the three blocks used in DFS implementation i.e. validate node, mark visited node and traverse neighboring nodes.

We’ll just make one slight modification. Instead of recursive traversal, we’ll use a FIFO data structure to track neighbors and iterate over them:

public List<Coordinate> solve(Maze maze) {
    LinkedList<Coordinate> nextToVisit 
      = new LinkedList<>();
    Coordinate start = maze.getEntry();
    nextToVisit.add(start);

    while (!nextToVisit.isEmpty()) {
        Coordinate cur = nextToVisit.remove();

        if (!maze.isValidLocation(cur.getX(), cur.getY()) 
          || maze.isExplored(cur.getX(), cur.getY())
        ) {
            continue;
        }

        if (maze.isWall(cur.getX(), cur.getY())) {
            maze.setVisited(cur.getX(), cur.getY(), true);
            continue;
        }

        if (maze.isExit(cur.getX(), cur.getY())) {
            return backtrackPath(cur);
        }

        for (int[] direction : DIRECTIONS) {
            Coordinate coordinate 
              = new Coordinate(
                cur.getX() + direction[0], 
                cur.getY() + direction[1], 
                cur
              );
            nextToVisit.add(coordinate);
            maze.setVisited(cur.getX(), cur.getY(), true);
        }
    }
    return Collections.emptyList();
}

5. Conclusion

In this tutorial, we described two major graph algorithms Depth-first search and Breadth-first search to solve a maze. We also touched upon how BFS gives the shortest path from the entry to the exit.

For further reading, look up other methods to solve a maze, like A* and Dijkstra algorithm.