1. Introduction
A set is a handy way to represent a unique collection of items.
In this tutorial, we’ll learn more about what that means and how we can use one in Java.
2. A Bit of Set Theory
2.1. What Is a Set?
A set is simply a group of unique things. So, a significant characteristic of any set is that it does not contain duplicates.
We can put anything we like into a set. However, we typically use sets to group together things which have a common trait. For example, we could have a set of vehicles or a set of animals.
Let’s use two sets of integers as a simple example:
setA : {1, 2, 3, 4}
setB : {2, 4, 6, 8}
We can show sets as a diagram by simply putting the values into circles:
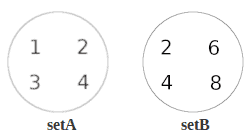
Diagrams like these are known as Venn diagrams and give us a useful way to show interactions between sets as we’ll see later.
2.2. The Intersection of Sets
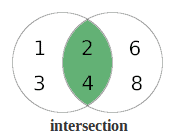
The term intersection means the common values of different sets.
We can see that the integers 2 and 4 exist in both sets. So the intersection of setA and setB is 2 and 4 because these are the values which are common to both of our sets.
setA intersection setB = {2, 4}
In order to show the intersection in a diagram, we merge our two sets and highlight the area that is common to both of our sets:
2.3. The Union of Sets
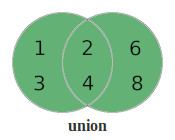
The term union means combining the values of different sets.
So let’s create a new set which is the union of our example sets. We already know that we can’t have duplicate values in a set. However, our sets have some duplicate values (2 and 4). So when we combine the contents of both sets, we need to ensure we remove duplicates. So we end up with 1, 2, 3, 4, 6 and 8.
setA union setB = {1, 2, 3, 4, 6, 8}
Again we can show the union in a diagram. So let’s merge our two sets and highlight the area that represents the union:
2.4. The Relative Complement of Sets
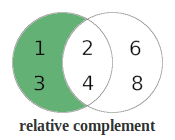
The term relative complement means the values from one set that are not in another. It is also referred to as the set difference.
Now let’s create new sets which are the relative complements of setA and setB.
relative complement of setA in setB = {6, 8}
relative complement of setB in setA = {1, 3}
And now, let’s highlight the area in setA that is not part of setB. This gives us the relative complement of setB in setA:
2.5. The Subset and Superset
A subset is simply part of a larger set, and the larger set is called a superset. When we have a subset and superset, the union of the two is equal to the superset, and the intersection is equal to the subset.
3. Implementing Set Operations With java.util.Set
In order to see how we perform set operations in Java, we’ll take the example sets and implement the intersection, union and relative complement. So let’s start by creating our sample sets of integers:
private Set<Integer> setA = setOf(1,2,3,4);
private Set<Integer> setB = setOf(2,4,6,8);
private static Set<Integer> setOf(Integer... values) {
return new HashSet<Integer>(Arrays.asList(values));
}
3.1. Intersection
First, we’re going to use the retainAll method to create the intersection of our sample sets. Because retainAll modifies the set directly, we’ll make a copy of setA called intersectSet. Then we’ll use the retainAll method to keep the values that are also in setB:
Set<Integer> intersectSet = new HashSet<>(setA);
intersectSet.retainAll(setB);
assertEquals(setOf(2,4), intersectSet);
3.2. Union
Now let’s use the addAll method to create the union of our sample sets. The addAll method adds all the members of the supplied set to the other. Again as addAll updates the set directly, we’ll make a copy of setA called unionSet, and then add setB to it:
Set<Integer> unionSet = new HashSet<>(setA);
unionSet.addAll(setB);
assertEquals(setOf(1,2,3,4,6,8), unionSet);
3.3. Relative Complement
Finally, we’ll use the removeAll method to create the relative complement of setB in setA. We know that we want the values that are in setA that don’t exist in setB. So we just need to removeAll elements from setA that are also in setB:
Set<Integer> differenceSet = new HashSet<>(setA);
differenceSet.removeAll(setB);
assertEquals(setOf(1,3), differenceSet);
4. Implementing Set Operations with Streams
4.1. Intersection
Let’s create the intersection of our sets using Streams.
First, we’ll get the values from setA into a stream. Then we’ll filter the stream to keep all values that are also in setB. And lastly, we’ll collect the results into a new Set:
Set<Integer> intersectSet = setA.stream()
.filter(setB::contains)
.collect(Collectors.toSet());
assertEquals(setOf(2,4), intersectSet);
4.2. Union
Now let’s use the static method Streams.concat to add the values of our sets into a single stream.
In order to get the union from the concatenation of our sets, we need to remove any duplicates. We’ll do this by simply collecting the results into a Set:
Set<Integer> unionSet = Stream.concat(setA.stream(), setB.stream())
.collect(Collectors.toSet());
assertEquals(setOf(1,2,3,4,6,8), unionSet);
4.3. Relative Complement
Finally, we’ll create the relative complement of setB in setA.
As we did with the intersection example we’ll first get the values from setA into a stream. This time we’ll filter the stream to remove any values that are also in setB. Then, we’ll collect the results into a new Set:
Set<Integer> differenceSet = setA.stream()
.filter(val -> !setB.contains(val))
.collect(Collectors.toSet());
assertEquals(setOf(1,3), differenceSet);
5. Utility Libraries for Set Operations
Now that we’ve seen how to perform basic set operations with pure Java, let’s use a couple of utility libraries to perform the same operations. One nice thing about using these libraries is that the method names clearly tell us what operation is being performed.
5.1. Dependencies
In order to use the Guava Sets and Apache Commons Collections SetUtils we need to add their dependencies:
<dependency>
<groupId>com.google.guava</groupId>
<artifactId>guava</artifactId>
<version>31.0.1-jre</version>
</dependency>
<dependency>
<groupId>org.apache.commons</groupId>
<artifactId>commons-collections4</artifactId>
<version>4.3</version>
</dependency>
5.2. Guava Sets
Let’s use the Guava Sets class to perform intersection and union on our example sets. In order to do this we can simply use the static methods union and intersection of the Sets class:
Set<Integer> intersectSet = Sets.intersection(setA, setB);
assertEquals(setOf(2,4), intersectSet);
Set<Integer> unionSet = Sets.union(setA, setB);
assertEquals(setOf(1,2,3,4,6,8), unionSet);
Take a look at our Guava Sets article to find out more.
5.3. Apache Commons Collections
Now let’s use the intersection and union static methods of the SetUtils class from the Apache Commons Collections:
Set<Integer> intersectSet = SetUtils.intersection(setA, setB);
assertEquals(setOf(2,4), intersectSet);
Set<Integer> unionSet = SetUtils.union(setA, setB);
assertEquals(setOf(1,2,3,4,6,8), unionSet);
Take a look at our Apache Commons Collections SetUtils tutorial to find out more.
6. Conclusion
We’ve seen an overview of how to perform some basic operations on sets, as well as details of how to implement these operations in a number of different ways.
All of the code examples can be found over on GitHub.









