Rotate Arrays in Java

1. Overview

In this tutorial, we’ll learn some algorithms for array rotation in Java.

We’ll see how to rotate the array elements k times to the right. We’ll also understand how to modify the array in place, although we might use extra space to compute the rotation.

2. Introduction to Array Rotation

Before digging into some solutions, let’s discuss how to start thinking about the algorithm.

We’ll alias the rotation number with the letter k.

2.1. Find the Smallest Rotation

We’ll transform k to the remainder of k divided by the array length, or k modulo (%) of the array length. This allows us to translate a large rotation number to a relatively small one.

2.2. Unit Testing

We might want to test k less than, equal to, and greater than the array length. For example, if we rotate 8 times an array of 6 elements, we’ll need only a 2-cycle rotation.

Similarly, we shouldn’t modify the array if k is equal to the array length. Thus, this is something we need to consider as an edge case.

Finally, we should also check whether the input array isn’t null or k is greater than zero.

2.3. Array and Rotation Testing Variables

We’ll set the following variables:

• arr as the array to test length 6
• rotationLtArrayLength = 1 as a rotation less than the array length
• rotationGtArrayLength = 8 as a rotation greater than the array length
• ltArrayLengthRotation as the solution for rotationLtArrayLength
• gtArrayLengthRotation as the solution for rotationGtArrayLength

Let’s look at their initial values:

int[] arr = { 1, 2, 3, 4, 5, 6 };
int rotationLtArrayLength = 1;
int rotationGtArrayLength = arr.length + 2;
int[] ltArrayLengthRotation = { 6, 1, 2, 3, 4, 5 };
int[] gtArrayLengthRotation = { 5, 6, 1, 2, 3, 4 };

2.4. Space and Time Complexity

Nonetheless, we must be confident with time and space complexity concepts to understand the algorithm solution.

3. Brute Force

It’s a common approach to try solving a problem with brute force. This might not be an efficient solution. However, it helps to understand the problem space.

3.1. Algorithm

We solve by rotating in k steps while shifting the elements by one unit in each step.

Let’s have a look at the method:

void bruteForce(int[] arr, int k) {
    // check invalid input
    k %= arr.length;
    int temp;
    int previous;
    for (int i = 0; i < k; i++) {
        previous = arr[arr.length - 1];
        for (int j = 0; j < arr.length; j++) {
            temp = arr[j];
            arr[j] = previous;
            previous = temp;
        }
    }
}

3.2. Code Insight

We iterate over the array length twice with a nested loop. At first, we get a value we want to rotate at index i:

for (int i = 0; i < k; i++) {
    previous = arr[arr.length - 1];
    // nested loop
}

Then, we shift all the elements in the nested for loop by one using a temporary variable.

for (int j = 0; j < arr.length; j++) {
    temp = arr[j];
    arr[j] = previous;
    previous = temp;
}

3.3. Complexity Analysis

• Time complexity: O(n×k). All the numbers are shifted by one step O(n) for k times.
• Space complexity: O(1). Constant extra space is used.

3.4. Unit Test

Let’s write a test for the brute force algorithm when k is less than the array length:

@Test
void givenInputArray_whenUseBruteForceRotationLtArrayLength_thenRotateArrayOk() {
    bruteForce(arr, rotationLtArrayLength);
    assertArrayEquals(ltArrayLengthRotation, arr);
}

Likewise, we test k greater than the array length:

@Test
void givenInputArray_whenUseBruteForceRotationGtArrayLength_thenRotateArrayOk() {
    bruteForce(arr, rotationGtArrayLength);
    assertArrayEquals(gtArrayLengthRotation, arr);
}

Finally, let’s test k equal to the array length:

@Test
void givenInputArray_whenUseBruteForceRotationEqArrayLength_thenDoNothing() {
    int[] expected = arr.clone();
    bruteForce(arr, arr.length);
    assertArrayEquals(expected, arr);
}

4. Rotation With Extra Array

We use an extra array to place every element at its correct position. Then, we copy back to the original one.

4.1. Algorithm

To get the rotated position, we’ll find the (i +k ) position module (%) of the array length:

void withExtraArray(int[] arr, int k) {
    // check invalid input

    int[] extraArray = new int[arr.length];
    for (int i = 0; i < arr.length; i++) {
        extraArray[(i + k) % arr.length] = arr[i];
    }
    System.arraycopy(extraArray, 0, arr, 0, arr.length);
}

Notably, although not required, we could return the extra array.

4.2. Code Insight

We move every element from i to the (i + k) % arr.length position in an extra space array.

Finally, we copy it to the original one using System.arraycopy().

4.3. Complexity Analysis

• Time complexity: O$(n)$. We have one pass to apply rotation in the new array from which we copy, in another step, over to the original one.
• Space complexity: O(n). We use another array of the same size to store the rotation.

4.4. Unit Test

Let’s test the rotation with this extra array algorithm when k is less than the array length:

@Test
void givenInputArray_whenUseExtraArrayRotationLtArrayLength_thenRotateArrayOk() {
    withExtraArray(arr, rotationLtArrayLength);
    assertArrayEquals(ltArrayLengthRotation, arr);
}

Likewise, we test k greater than the array length:

@Test
void givenInputArray_whenUseExtraArrayRotationGtArrayLength_thenRotateArrayOk() {
    withExtraArray(arr, rotationGtArrayLength);
    assertArrayEquals(gtArrayLengthRotation, arr);
}

Finally, let’s test k equal to the array length:

@Test
void givenInputArray_whenUseExtraArrayWithRotationEqArrayLength_thenDoNothing() {
    int[] expected = arr.clone();
    withExtraArray(arr, arr.length);
    assertArrayEquals(expected, arr);
}

5. Cyclic Replacements

We could replace an element at its required position every time. However, we’d lose the original value. Therefore, we’ll store it in a temporary variable. Then, we can place the rotated element for n times, where n is the array length.

5.1. Algorithm

We can see the logic of the cyclic replacement in the diagram for k = 2:

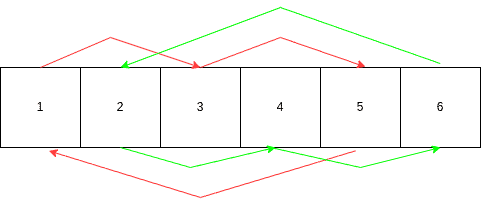
So, we start from the index 0 and do 2-step cycles.

However, there is an issue with this approach. As we might notice, we can return to the initial array position. In that case, we’ll start again as a regular for-loop cycle.

Finally, we’ll keep track of the elements we replaced using a count variable. Our cycle will complete when the count is equal to the array length.

Let’s look at the code:

void cyclicReplacement(int[] arr, int k) {
    // check invalid input

    k = k % arr.length;
    int count = 0;
    for (int start = 0; count < arr.length; start++) {
        int current = start;
        int prev = arr[start];
        do {
            int next = (current + k) % arr.length;
            int temp = arr[next];
            arr[next] = prev;
            prev = temp;
            current = next;
            count++;
        } while (start != current);
    }
}

5.2. Code Insight

There are two parts we need to focus on for this algorithm.

The first one is the outer loop. We iterate for every n/k fraction of elements we replace in a k-step cycle:

for (int start = 0; count < arr.length; start++) {
    int current = start;
    int prev = arr[start];
    do {
        // do loop
    } while (start != current);
}

Therefore, we use a do-while-loop to shift a value by k steps (while saving the replaced value) until we reach the number from which we originally started and go back to the outer loop:

int next = (current + k) % arr.length;
int temp = arr[next];
arr[next] = prev;
prev = temp;
current = next;
count++;

5.3. Complexity Analysis

• Time complexity: O(n)
• Space complexity: O(1). Constant extra space is used.

5.4. Unit Test

Let’s test the cyclic replacement array algorithm when k is less than the array length:

@Test
void givenInputArray_whenUseCyclicReplacementRotationLtArrayLength_thenRotateArrayOk() {
    cyclicReplacement(arr, rotationLtArrayLength);
    assertArrayEquals(ltArrayLengthRotation, arr);
}

Likewise, we test k greater than the array length:

@Test
void givenInputArray_whenUseCyclicReplacementRotationGtArrayLength_thenRotateArrayOk() {
    cyclicReplacement(arr, rotationGtArrayLength);
    assertArrayEquals(gtArrayLengthRotation, arr);
}

Finally, let’s test k equal to the array length:

@Test
void givenInputArray_whenUseCyclicReplacementRotationEqArrayLength_thenDoNothing() {
    int[] expected = arr.clone();
    cyclicReplacement(arr, arr.length);
    assertArrayEquals(expected, arr);
}

6. Reverse

This is a simple yet non-trivial algorithm. When we rotate, we might notice that k elements from the back end of the array come to the front, and the rest of the elements from the front shift backward.

6.1. Algorithm

We solve with three steps in which we reverse:

• All the elements of the array
• The first k elements
• The remaining (n-k) elements

Let’s have a look at the code:

void reverse(int[] arr, int k) {
    // check invalid input

    k %= arr.length;
    reverse(arr, 0, arr.length - 1);
    reverse(arr, 0, k - 1);
    reverse(arr, k, arr.length - 1);
}

void reverse(int[] nums, int start, int end) {
    while (start < end) {
        int temp = nums[start];
        nums[start] = nums[end];
        nums[end] = temp;
        start++;
        end--;
    }
}

6.2. Code Insight

We use a helper method similar to brute force’s nested loop. However, we do it in three different steps this time:

We reverse the whole array:

reverse(arr, 0, arr.length - 1);

Then, we reverse the first k elements.

reverse(arr, 0, k - 1);

Finally, we reverse the remaining elements:

reverse(arr, k, arr.length - 1);

Although this seems to introduce redundancy, it’ll allow us to complete the task in linear time.

6.3. Complexity Analysis

• Time complexity: O(n). n elements are reversed a total of three times.
• Space complexity: O(1). Constant extra space is used.

6.4. Unit Test

Let’s test the reverse algorithm when k is less than the array length:

@Test
void givenInputArray_whenUseReverseRotationLtArrayLength_thenRotateArrayOk() {
    reverse(arr, rotationLtArrayLength);
    assertArrayEquals(ltArrayLengthRotation, arr);
}

Likewise, we test k greater than the array length:

@Test
void givenInputArray_whenUseReverseRotationGtArrayLength_thenRotateArrayOk() {
    reverse(arr, rotationGtArrayLength);
    assertArrayEquals(gtArrayLengthRotation, arr);
}

Finally, let’s test k equal to the array length:

@Test
void givenInputArray_whenUseReverseRotationEqArrayLength_thenDoNothing() {
    int[] expected = arr.clone();
    reverse(arr, arr.length);
    assertArrayEquals(expected, arr);
}

7. Conclusion

In this article, we saw how to rotate an array by k rotations. We started with brute force and then moved to more complex algorithms like reverse or cyclic replacements with no extra space. We also talked about the time and space complexity. Finally, we discussed unit testing and some edge cases.

As always, the code presented in this article is available over on GitHub.