Obtaining a Power Set of a Set in Java

1. Introduction

In this tutorial, we’ll study the process of generating a power set of a given set in Java.

As a quick reminder, for every set of size n, there is a power set of size 2ⁿ. We’ll learn how to get it using various techniques.

2. Definition of a Power Set

The power set of a given set S is the set of all subsets of S, including S itself and the empty set.

For example, for a given set:

{"APPLE", "ORANGE", "MANGO"}

the power set is:

{
    {},
    {"APPLE"},
    {"ORANGE"},
    {"APPLE", "ORANGE"},
    {"MANGO"},
    {"APPLE", "MANGO"},
    {"ORANGE", "MANGO"},
    {"APPLE", "ORANGE", "MANGO"}
}

As it is also a set of subsets, the order of its internal subsets is not important and they can appear in any order:

{
    {},
    {"MANGO"},
    {"ORANGE"},
    {"ORANGE", "MANGO"},
    {"APPLE"},
    {"APPLE", "MANGO"},
    {"APPLE", "ORANGE"},
    {"APPLE", "ORANGE", "MANGO"}
}

3. Guava Library

The Google Guava library has some useful Set utilities, such as the power set. Thus, we can easily use it to get the power set of the given set, too:

@Test
public void givenSet_WhenGuavaLibraryGeneratePowerSet_ThenItContainsAllSubsets() {
    ImmutableSet<String> set = ImmutableSet.of("APPLE", "ORANGE", "MANGO");
    Set<Set<String>> powerSet = Sets.powerSet(set);
    Assertions.assertEquals((1 << set.size()), powerSet.size());
    MatcherAssert.assertThat(powerSet, Matchers.containsInAnyOrder(
      ImmutableSet.of(),
      ImmutableSet.of("APPLE"),
      ImmutableSet.of("ORANGE"),
      ImmutableSet.of("APPLE", "ORANGE"),
      ImmutableSet.of("MANGO"),
      ImmutableSet.of("APPLE", "MANGO"),
      ImmutableSet.of("ORANGE", "MANGO"),
      ImmutableSet.of("APPLE", "ORANGE", "MANGO")
   ));
}

Guava powerSet internally operates over the Iterator interface in the way when the next subset is requested, the subset is calculated and returned. So, the space complexity is reduced to O(n) instead of O(2ⁿ).

But, how does Guava achieve this?

4. Power Set Generation Approach

4.1. Algorithm

Let’s now discuss the possible steps for creating an algorithm for this operation.

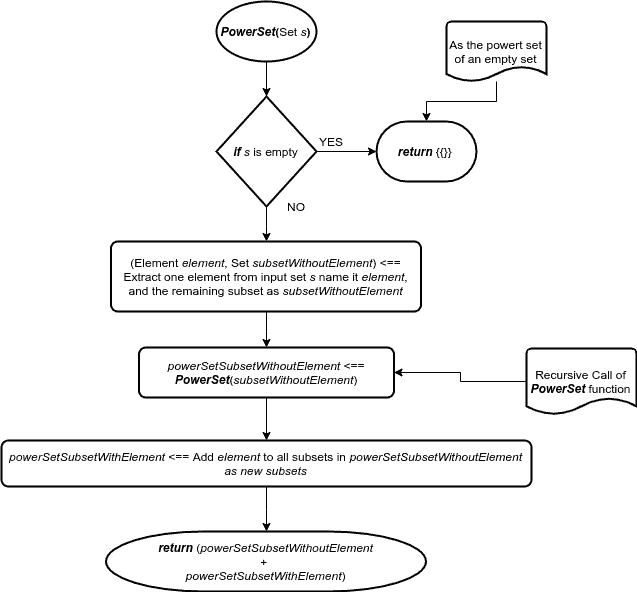
The power set of an empty set is {{}} in which it contains only one empty set, so that’s our simplest case.

For every set S other than the empty set, we first extract one element and name it – element. Then, for the rest of the elements of a set subsetWithoutElement, we calculate their power set recursively – and name it something like powerSetSubsetWithoutElement. Then, by adding the extracted element to all sets in powerSetSubsetWithoutElement, we get powerSetSubsetWithElement.

Now, the power set S is the union of a powerSetSubsetWithoutElement and a powerSetSubsetWithElement:

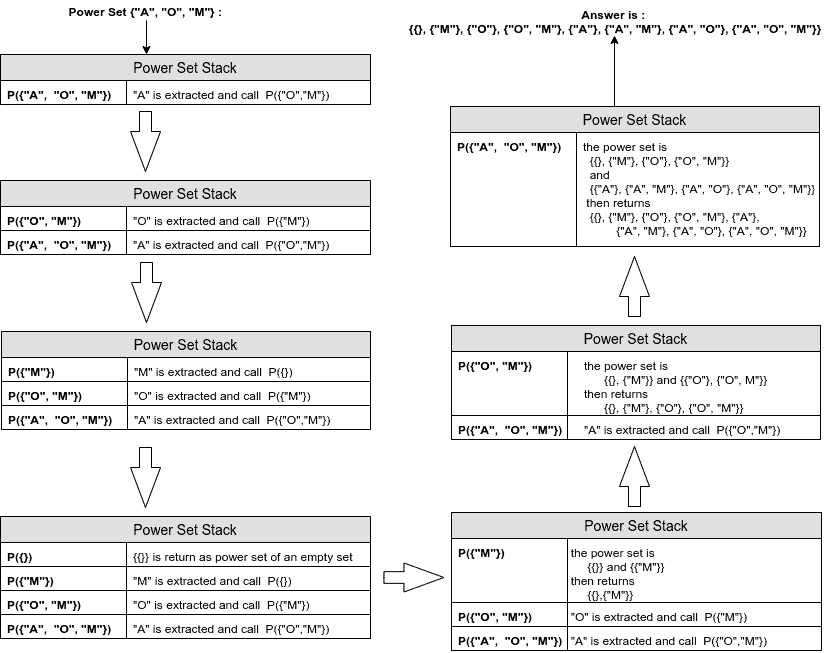
Let’s see an example of the recursive power set stack for the given set {“APPLE”, “ORANGE”, “MANGO”}.

To improve the readability of the image we use short forms of names: P means power set function and “A”, “O”, “M” are short forms of “APPLE”, “ORANGE”, and “MANGO”, respectively:

4.2. Implementation

So, first, let’s write the Java code for extracting one element and get the remaining subsets:

T element = set.iterator().next();
Set<T> subsetWithoutElement = new HashSet<>();
for (T s : set) {
    if (!s.equals(element)) {
        subsetWithoutElement.add(s);
    }
}

We’ll then want to get the powerset of subsetWithoutElement:

Set<Set<T>> powersetSubSetWithoutElement = recursivePowerSet(subsetWithoutElement);

Next, we need to add that powerset back into the original:

Set<Set<T>> powersetSubSetWithElement = new HashSet<>();
for (Set<T> subsetWithoutElement : powerSetSubSetWithoutElement) {
    Set<T> subsetWithElement = new HashSet<>(subsetWithoutElement);
    subsetWithElement.add(element);
    powerSetSubSetWithElement.add(subsetWithElement);
}

Finally the union of powerSetSubSetWithoutElement and powerSetSubSetWithElement is the power set of the given input set:

Set<Set<T>> powerSet = new HashSet<>();
powerSet.addAll(powerSetSubSetWithoutElement);
powerSet.addAll(powerSetSubSetWithElement);

If we put all our code snippets together, we can see our final product:

public Set<Set<T>> recursivePowerSet(Set<T> set) {
    if (set.isEmpty()) {
        Set<Set<T>> ret = new HashSet<>();
        ret.add(set);
        return ret;
    }

    T element = set.iterator().next();
    Set<T> subSetWithoutElement = getSubSetWithoutElement(set, element);
    Set<Set<T>> powerSetSubSetWithoutElement = recursivePowerSet(subSetWithoutElement);
    Set<Set<T>> powerSetSubSetWithElement = addElementToAll(powerSetSubSetWithoutElement, element);

    Set<Set<T>> powerSet = new HashSet<>();
    powerSet.addAll(powerSetSubSetWithoutElement);
    powerSet.addAll(powerSetSubSetWithElement);
    return powerSet;
}

4.3. Notes for Unit Tests

Now let’s test. We’ve got a bit of criteria here to confirm:

• First, we check the size of the power set and it must be 2ⁿ for a set of size n.
• Then, every element will occur only one time in a subset and 2^n-1 different subsets.
• Finally, every subset must appear once.

If all these conditions passed, we can be sure that our function works. Now, since we’ve used Set<Set>, we already know that there’s no repetition. In that case, we only need to check the size of the power set, and the number of occurrences of each element in the subsets.

To check the size of the power set we can use:

MatcherAssert.assertThat(powerSet, IsCollectionWithSize.hasSize((1 << set.size())));

And to check the number of occurrences of each element:

Map<String, Integer> counter = new HashMap<>();
for (Set<String> subset : powerSet) { 
    for (String name : subset) {
        int num = counter.getOrDefault(name, 0);
        counter.put(name, num + 1);
    }
}
counter.forEach((k, v) -> Assertions.assertEquals((1 << (set.size() - 1)), v.intValue()));

Finally, if we can put all together into one unit test:

@Test
public void givenSet_WhenPowerSetIsCalculated_ThenItContainsAllSubsets() {
    Set<String> set = RandomSetOfStringGenerator.generateRandomSet();
    Set<Set<String>> powerSet = new PowerSet<String>().recursivePowerSet(set);
    MatcherAssert.assertThat(powerSet, IsCollectionWithSize.hasSize((1 << set.size())));
   
    Map<String, Integer> counter = new HashMap<>();
    for (Set<String> subset : powerSet) {
        for (String name : subset) {
            int num = counter.getOrDefault(name, 0);
            counter.put(name, num + 1);
        }
    }
    counter.forEach((k, v) -> Assertions.assertEquals((1 << (set.size() - 1)), v.intValue()));
}

5. Optimization

In this section, we’ll try to minimize the space and reduce the number of internal operations to calculate the power set in an optimal way.

5.1. Data Structure

As we can see in the given approach, we need a lot of subtractions in the recursive call, which consumes a large amount of time and memory.

Instead, we can map each set or subset to some other notions to reduce the number of operations.

First, we need to assign an increasing number starting from 0 to each object in the given set S which means we work with an ordered list of numbers.

For example for the given set {“APPLE”, “ORANGE”, “MANGO”} we get:

“APPLE” -> 0

“ORANGE” -> 1

“MANGO” -> 2

So, from now on, instead of generating subsets of S, we generate them for the ordered list of [0, 1, 2], and as it is ordered we can simulate subtractions by a starting index.

For example, if the starting index is 1 it means that we generate the power set of [1,2].

To retrieve mapped id from the object and vice-versa, we store both sides of mapping. Using our example, we store both (“MANGO” -> 2) and (2 -> “MANGO”). As the mapping of numbers started from zero, so for the reverse map there we can use a simple array to retrieve the respective object.

One of the possible implementations of this function would be:

private Map<T, Integer> map = new HashMap<>();
private List<T> reverseMap = new ArrayList<>();

private void initializeMap(Collection<T> collection) {
    int mapId = 0;
    for (T c : collection) {
        map.put(c, mapId++);
        reverseMap.add(c);
    }
}

Now, to represent subsets there are two well-known ideas:

1. Index representation
2. Binary representation

5.2. Index Representation

Each subset is represented by the index of its values. For example, the index mapping of the given set {“APPLE”, “ORANGE”, “MANGO”} would be:

{
   {} -> {}
   [0] -> {"APPLE"}
   [1] -> {"ORANGE"}
   [0,1] -> {"APPLE", "ORANGE"}
   [2] -> {"MANGO"}
   [0,2] -> {"APPLE", "MANGO"}
   [1,2] -> {"ORANGE", "MANGO"}
   [0,1,2] -> {"APPLE", "ORANGE", "MANGO"}
}

So, we can retrieve the respective set from a subset of indices with the given mapping:

private Set<Set<T>> unMapIndex(Set<Set<Integer>> sets) {
    Set<Set<T>> ret = new HashSet<>();
    for (Set<Integer> s : sets) {
        HashSet<T> subset = new HashSet<>();
        for (Integer i : s) {
            subset.add(reverseMap.get(i));
        }
        ret.add(subset);
    }
    return ret;
}

5.3. Binary Representation

Or, we can represent each subset using binary. If an element of the actual set exists in this subset its respective value is 1; otherwise it is 0.

For our fruit example, the power set would be:

{
    [0,0,0] -> {}
    [1,0,0] -> {"APPLE"}
    [0,1,0] -> {"ORANGE"}
    [1,1,0] -> {"APPLE", "ORANGE"}
    [0,0,1] -> {"MANGO"}
    [1,0,1] -> {"APPLE", "MANGO"}
    [0,1,1] -> {"ORANGE", "MANGO"}
    [1,1,1] -> {"APPLE", "ORANGE", "MANGO"}
}

So, we can retrieve the respective set from a binary subset with the given mapping:

private Set<Set<T>> unMapBinary(Collection<List<Boolean>> sets) {
    Set<Set<T>> ret = new HashSet<>();
    for (List<Boolean> s : sets) {
        HashSet<T> subset = new HashSet<>();
        for (int i = 0; i < s.size(); i++) {
            if (s.get(i)) {
                subset.add(reverseMap.get(i));
            }
        }
        ret.add(subset);
    }
    return ret;
}

5.4. Recursive Algorithm Implementation

In this step, we’ll try to implement the previous code using both data structures.

Before calling one of these functions, we need to call the initializeMap method to get the ordered list. Also, after creating our data structure, we need to call the respective unMap function to retrieve the actual objects:

public Set<Set<T>> recursivePowerSetIndexRepresentation(Collection<T> set) {
    initializeMap(set);
    Set<Set<Integer>> powerSetIndices = recursivePowerSetIndexRepresentation(0, set.size());
    return unMapIndex(powerSetIndices);
}

So, let’s try our hand at the index representation:

private Set<Set<Integer>> recursivePowerSetIndexRepresentation(int idx, int n) {
    if (idx == n) {
        Set<Set<Integer>> empty = new HashSet<>();
        empty.add(new HashSet<>());
        return empty;
    }
    Set<Set<Integer>> powerSetSubset = recursivePowerSetIndexRepresentation(idx + 1, n);
    Set<Set<Integer>> powerSet = new HashSet<>(powerSetSubset);
    for (Set<Integer> s : powerSetSubset) {
        HashSet<Integer> subSetIdxInclusive = new HashSet<>(s);
        subSetIdxInclusive.add(idx);
        powerSet.add(subSetIdxInclusive);
    }
    return powerSet;
}

Now, let’s see the binary approach:

private Set<List<Boolean>> recursivePowerSetBinaryRepresentation(int idx, int n) {
    if (idx == n) {
        Set<List<Boolean>> powerSetOfEmptySet = new HashSet<>();
        powerSetOfEmptySet.add(Arrays.asList(new Boolean[n]));
        return powerSetOfEmptySet;
    }
    Set<List<Boolean>> powerSetSubset = recursivePowerSetBinaryRepresentation(idx + 1, n);
    Set<List<Boolean>> powerSet = new HashSet<>();
    for (List<Boolean> s : powerSetSubset) {
        List<Boolean> subSetIdxExclusive = new ArrayList<>(s);
        subSetIdxExclusive.set(idx, false);
        powerSet.add(subSetIdxExclusive);
        List<Boolean> subSetIdxInclusive = new ArrayList<>(s);
        subSetIdxInclusive.set(idx, true);
        powerSet.add(subSetIdxInclusive);
    }
    return powerSet;
}

5.5. Iterate Through [0, 2ⁿ)

Now, there is a nice optimization we can do with the binary representation. If we look at it, we can see that each row is equivalent to the binary format of a number in [0, 2ⁿ).

So, if we iterate through numbers from 0 to 2ⁿ, we can convert that index to binary, and use it to create a boolean representation of each subset:

private List<List<Boolean>> iterativePowerSetByLoopOverNumbers(int n) {
    List<List<Boolean>> powerSet = new ArrayList<>();
    for (int i = 0; i < (1 << n); i++) {
        List<Boolean> subset = new ArrayList<>(n);
        for (int j = 0; j < n; j++)
            subset.add(((1 << j) & i) > 0);
        powerSet.add(subset);
    }
    return powerSet;
}

5.6. Minimal Change Subsets by Gray Code

Now, if we define any bijective function from binary representation of length n to a number in [0, 2ⁿ), we can generate subsets in any order that we want.

Gray Code is a well-known function that is used to generate binary representations of numbers so that the binary representation of consecutive numbers differ by only one bit (even the difference of the last and first numbers is one).

We can thus optimize this just a bit further:

private List<List<Boolean>> iterativePowerSetByLoopOverNumbersWithGrayCodeOrder(int n) {
    List<List<Boolean>> powerSet = new ArrayList<>();
    for (int i = 0; i < (1 << n); i++) {
        List<Boolean> subset = new ArrayList<>(n);
        for (int j = 0; j < n; j++) {
            int grayEquivalent = i ^ (i >> 1);
            subset.add(((1 << j) & grayEquivalent) > 0);
        }
        powerSet.add(subset);
    }
    return powerSet;
}

6. Lazy Loading

To minimize the space usage of power set, which is O(2ⁿ), we can utilize the Iterator interface to fetch every subset, and also every element in each subset lazily.

6.1. ListIterator

First, to be able to iterate from 0 to 2ⁿ, we should have a special Iterator that loops over this range but not consuming the whole range beforehand.

To solve this problem, we’ll use two variables; one for the size, which is 2ⁿ, and another for the current subset index. Our hasNext() function will check that position is less than size:

abstract class ListIterator<K> implements Iterator<K> {
    protected int position = 0;
    private int size;
    public ListIterator(int size) {
        this.size = size;
    }
    @Override
    public boolean hasNext() {
        return position < size;
    }
}

And our next() function returns the subset for the current position and increases the value of position by one:

@Override
public Set<E> next() {
    return new Subset<>(map, reverseMap, position++);
}

6.2. Subset

To have a lazy load Subset, we define a class that extends AbstractSet, and we override some of its functions.

By looping over all bits that are 1 in the receiving mask (or position) of the Subset, we can implement the Iterator and other methods in AbstractSet.

For example, the size() is the number of 1s in the receiving mask:

@Override
public int size() { 
    return Integer.bitCount(mask);
}

And the contains() function is just whether the respective bit in the mask is 1 or not:

@Override
public boolean contains(@Nullable Object o) {
    Integer index = map.get(o);
    return index != null && (mask & (1 << index)) != 0;
}

We use another variable – remainingSetBits – to modify it whenever we retrieve its respective element in the subset we change that bit to 0. Then, the hasNext() checks if remainingSetBits is not zero (that is, it has at least one bit with a value of 1):

@Override
public boolean hasNext() {
    return remainingSetBits != 0;
}

And the next() function uses the right-most 1 in the remainingSetBits, then converts it to 0, and also returns the respective element:

@Override
public E next() {
    int index = Integer.numberOfTrailingZeros(remainingSetBits);
    if (index == 32) {
        throw new NoSuchElementException();
    }
    remainingSetBits &= ~(1 << index);
    return reverseMap.get(index);
}

6.3. PowerSet

To have a lazy-load PowerSet class, we need a class that extends AbstractSet<Set<T>>.

The size() function is simply 2 to the power of the set’s size:

@Override
public int size() {
    return (1 << this.set.size());
}

As the power set will contain all possible subsets of the input set, so contains(Object o) function checks if all elements of the object o are existing in the reverseMap (or in the input set):

@Override
public boolean contains(@Nullable Object obj) {
    if (obj instanceof Set) {
        Set<?> set = (Set<?>) obj;
        return reverseMap.containsAll(set);
    }
    return false;
}

To check equality of a given Object with this class, we can only check if the input set is equal to the given Object:

@Override
public boolean equals(@Nullable Object obj) {
    if (obj instanceof PowerSet) {
        PowerSet<?> that = (PowerSet<?>) obj;
        return set.equals(that.set);
    }
    return super.equals(obj);
}

The iterator() function returns an instance of ListIterator that we defined already:

@Override
public Iterator<Set<E>> iterator() {
    return new ListIterator<Set<E>>(this.size()) {
        @Override
        public Set<E> next() {
            return new Subset<>(map, reverseMap, position++);
        }
    };
}

The Guava library uses this lazy-load idea and these PowerSet and Subset are the equivalent implementations of the Guava library.

For more information, check their source code and documentation.

Furthermore, if we want to do parallel operation over subsets in PowerSet, we can call Subset for different values in a ThreadPool.

7. Summary

To sum up, first, we studied what is a power set. Then, we generated it by using the Guava Library. After that, we studied the approach and how we should implement it, and also how to write a unit test for it.

Finally, we utilized the Iterator interface to optimize the space of generation of subsets and also their internal elements.