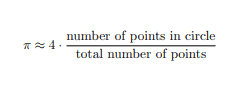1. Overview
Pi is the ratio of the circumference of a circle to the diameter of that circle. Irrespective of the size of any circle, the value of pi is approximately equal to 3.14159. It’s applicable in computations regarding circles.
In this tutorial, we’ll see how to calculate pi using Java. We’ll adopt the Monte Carlo algorithm to solve this task.
2. Monte Carlo Algorithm
Pi is an irrational number – it cannot be expressed as a simple fraction or definite decimal. We can calculate pi to any desired level of accuracy using various mathematical methods.
To begin with, the Monte Carlo method is one of the methods used to estimate the value of pi. This method uses random sampling to obtain a numerical solution to mathematical problems.
For example, let’s assume we have an empty canvas. Next, let’s draw a square on the canvas and a big circle inside the square. Then, let’s generate random points within the square. Some points will fall within the circle, while some will fall outside it. To estimate pi, we’ll count the total number of points and the total number of points within the circle. The diagram below describes the square, randomly generated points, and the inscribed circle:
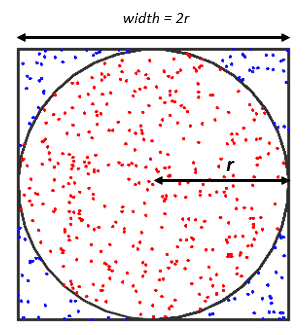
As we know, the area of a circle is pi multiplied by the radius square, and the area of a square inscribing the circle is four multiplied by the radius square. If we divide the area of a circle by the area of a square inscribing the circle, we’ll have pi divided by four. This ratio is also applicable to the number of points within the square and the number of points within the enclosed circle.
Therefore, let’s see the formula to estimate pi using the Monte Carlo method:
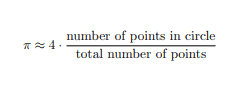
Next, we’ll implement the formula with Java.
3. Pi Java Program
Let’s see a simple Java program to calculate pi using the Monte Carlo algorithm:
@Test
void givenPiCalculator_whenCalculatePiWithTenThousandPoints_thenEstimatedPiIsWithinTolerance() {
int totalPoints = 10000;
int insideCircle = 0;
Random random = new Random();
for (long i = 0; i < totalPoints; i++) {
double x = random.nextDouble() * 2 - 1;
double y = random.nextDouble() * 2 - 1;
if (x * x + y * y <= 1) {
insideCircle++;
}
}
double pi = 4.0 * insideCircle / totalPoints;
assertEquals(Math.PI, pi, 0.01);
}
In the example above, we generate 10000 random points within a square of side length two centered at the origin.
Next, we check individual point to see if it falls within the circle. Any point within a distance of one from the origin is counted as being inside the circle.
Finally, we estimate the value of pi by finding the ratio of points inside the circle to the total number of points and multiplying the result by four.
4. Conclusion
In this article, we learned how to estimate the value of pi using the Monte Carlo algorithm. While there are some other mathematical methods to estimate pi, the Monte Carlo method is simple and easy to implement in Java.
As always, the complete example source code for the example is available over on GitHub.