1. Overview
In this short tutorial, we’ll see how we can efficiently merge sorted arrays using a heap.
2. The Algorithm
Since our problem statement is to use a heap to merge the arrays, we’ll use a min-heap to solve our problem. A min-heap is nothing but a binary tree in which the value of each node is smaller than the values of its child nodes.
Usually, the min-heap is implemented using an array in which the array satisfies specific rules when it comes to finding the parent and children of a node.
For an array A[] and an element at index i:
- A[(i-1)/2] will return its parent
- A[(2*i)+1] will return the left child
- A[(2*i)+2] will return the right child
Here’s a picture of min-heap and its array representation:
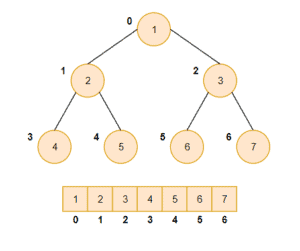
Let’s now create our algorithm that merges a set of sorted arrays:
- Create an array to store the results, with the size determined by adding the length of all the input arrays.
- Create a second array of size equal to the number of input arrays, and populate it with the first elements of all the input arrays.
- Transform the previously created array into a min-heap by applying the min-heap rules on all nodes and their children.
- Repeat the next steps until the result array is fully populated.
- Get the root element from the min-heap and store it in the result array.
- Replace the root element with the next element from the array in which the current root is populated.
- Apply min-heap rule again on our min-heap array.
Our algorithm has a recursive flow to create the min-heap, and we have to visit all the elements of the input arrays.
The time complexity of this algorithm is O(k log n), where k is the total number of elements in all the input arrays, and n is the total number of sorted arrays.
Let’s now see a sample input and the expected result after running the algorithm so that we can gain a better understanding of the problem. So for these arrays:
{ { 0, 6 }, { 1, 5, 10, 100 }, { 2, 4, 200, 650 } }
The algorithm should return a result array:
{ 0, 1, 2, 4, 5, 6, 10, 100, 200, 650 }
3. Java Implementation
Now that we have a basic understanding of what a min-heap is and how the merge algorithm works, let’s look at the Java implementation. We’ll use two classes — one to represent the heap nodes and the other to implement the merge algorithm.
3.1. Heap Node Representation
Before implementing the algorithm itself, let’s create a class that represents a heap node. This will store the node value and two supporting fields:
public class HeapNode {
int element;
int arrayIndex;
int nextElementIndex = 1;
public HeapNode(int element, int arrayIndex) {
this.element = element;
this.arrayIndex = arrayIndex;
}
}
Note that we’ve purposefully omitted the getters and setters here to keep things simple. We’ll use the arrayIndex property to store the index of the array in which the current heap node element is taken. And we’ll use the nextElementIndex property to store the index of the element that we’ll be taking after moving the root node to the result array.
Initially, the value of nextElementIndex will be 1. We’ll be incrementing its value after replacing the root node of the min-heap.
3.2. Min-Heap Merge Algorithm
Our next class is to represent the min-heap itself and to implement the merge algorithm:
public class MinHeap {
HeapNode[] heapNodes;
public MinHeap(HeapNode heapNodes[]) {
this.heapNodes = heapNodes;
heapifyFromLastLeafsParent();
}
int getParentNodeIndex(int index) {
return (index - 1) / 2;
}
int getLeftNodeIndex(int index) {
return (2 * index + 1);
}
int getRightNodeIndex(int index) {
return (2 * index + 2);
}
HeapNode getRootNode() {
return heapNodes[0];
}
// additional implementation methods
}
Now that we’ve created our min-heap class, let’s add a method that will heapify a subtree where the root node of the subtree is at the given index of the array:
void heapify(int index) {
int leftNodeIndex = getLeftNodeIndex(index);
int rightNodeIndex = getRightNodeIndex(index);
int smallestElementIndex = index;
if (leftNodeIndex < heapNodes.length
&& heapNodes[leftNodeIndex].element < heapNodes[index].element) {
smallestElementIndex = leftNodeIndex;
}
if (rightNodeIndex < heapNodes.length
&& heapNodes[rightNodeIndex].element < heapNodes[smallestElementIndex].element) {
smallestElementIndex = rightNodeIndex;
}
if (smallestElementIndex != index) {
swap(index, smallestElementIndex);
heapify(smallestElementIndex);
}
}
When we use an array to represent a min-heap, the last leaf node will always be at the end of the array. So when transforming an array into a min-heap by calling the heapify() method iteratively, we only need to start the iteration from the last leaf’s parent node:
void heapifyFromLastLeafsParent() {
int lastLeafsParentIndex = getParentNodeIndex(heapNodes.length);
while (lastLeafsParentIndex >= 0) {
heapify(lastLeafsParentIndex);
lastLeafsParentIndex--;
}
}
Our next method will do the actual implementation of our algorithm. For our better understanding, let’s split the method into two parts and see how it works:
int[] merge(int[][] array) {
// transform input arrays
// run the minheap algorithm
// return the resulting array
}
The first part transforms the input arrays into a heap node array that contains all the first array’s elements and finds the resulting array’s size:
HeapNode[] heapNodes = new HeapNode[array.length];
int resultingArraySize = 0;
for (int i = 0; i < array.length; i++) {
HeapNode node = new HeapNode(array[i][0], i);
heapNodes[i] = node;
resultingArraySize += array[i].length;
}
And the next part populates the result array by implementing the steps 4, 5, 6, and 7 of our algorithm:
MinHeap minHeap = new MinHeap(heapNodes);
int[] resultingArray = new int[resultingArraySize];
for (int i = 0; i < resultingArraySize; i++) {
HeapNode root = minHeap.getRootNode();
resultingArray[i] = root.element;
if (root.nextElementIndex < array[root.arrayIndex].length) {
root.element = array[root.arrayIndex][root.nextElementIndex++];
} else {
root.element = Integer.MAX_VALUE;
}
minHeap.heapify(0);
}
4. Testing the Algorithm
Let’s now test our algorithm with the same input we mentioned previously:
int[][] inputArray = { { 0, 6 }, { 1, 5, 10, 100 }, { 2, 4, 200, 650 } };
int[] expectedArray = { 0, 1, 2, 4, 5, 6, 10, 100, 200, 650 };
int[] resultArray = MinHeap.merge(inputArray);
assertThat(resultArray.length, is(equalTo(10)));
assertThat(resultArray, is(equalTo(expectedArray)));
5. Conclusion
In this tutorial, we learned how we can efficiently merge sorted arrays using min-heap.
The code backing this article is available on GitHub. Once you're
logged in as a Baeldung Pro Member, start learning and coding on the project.


















