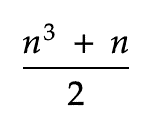Creating a Magic Square in Java

1. Introduction

In this article, we’re going to look at how to create a magic square. We’ll see what a magic square is, what the algorithms are for creating them and then how to implement this in Java.

2. What Is a Magic Square?

A magic square is a mathematical puzzle. We start out with a square of size n*n and need to fill it with numbers such that each number between 1 and n² is present exactly once, and that each row, column, and diagonal sum to the same number.

For example, a magic square of size 3*3 could be:

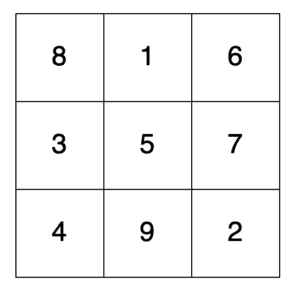
Here we can see that each cell has a different number, between 1 and 9. We can also see that each row, column, and diagonal sum to 15.

It happens that there’s an additional check here. The sum of each row, column, and diagonal also equals a value that can be calculated just by knowing n. Specifically:

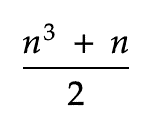
So, for our 3*3 square, this gives us a value of (3³ + 3)/2 = 15.

As it happens, there are three relatively simple algorithms that can be used to generate these, depending on the size of the square:

• Odd number of cells on each side
• Doubly: Even number of cells on each side. This is when each side is a multiple of 4.
• Singly: Even number of cells on each side. This is when each side is a multiple of 2 but not a multiple of 4.

We’ll look at each of these algorithms and how to generate them in Java in a bit.

3. Validating a Magic Square

Before we can generate our magic squares, we need to first be able to prove that a given square indeed meets the requirements. That is, each row, column, and diagonals sum to the same value.

Before we do this, let’s define a class to represent our square:

public class MagicSquare {
    private int[][] cells;
    
    public MagicSquare(int n) {
        this.cells = new int[n][];
        
        for (int i = 0; i < n; ++i) {
            this.cells[i] = new int[n];
        }
    }
    
    public int getN() {
        return cells.length;
    }
    
    public int getCell(int x, int y) {
        return cells[x][y];
    }
    
    public void setCell(int x, int y, int value) {
        cells[x][y] = value;
    }
}

This is just a wrapper around a 2-dimensional array of ints. We then ensure that the array is of the correct size and we have an easy way to access individual cells in the array.

Now that we have this, let’s write a method to validate that the square is indeed a magic square.

Firstly, we’ll calculate our expected value for the rows, columns, and diagonals to sum to:

int n = getN();
int expectedValue = ((n * n * n) + n) / 2;

Next, we’ll start summing values and checking that they come out as expected. We’ll do the diagonals first:

// Diagonals
if (IntStream.range(0, n).map(i -> getCell(i, i)).sum() != expectedValue) {
    throw new IllegalStateException("Leading diagonal is not the expected value");
}
if (IntStream.range(0, n).map(i -> getCell(i, n - i - 1)).sum() != expectedValue) {
    throw new IllegalStateException("Trailing diagonal is not the expected value");
}

This is just iterating from 0 to n, grabbing each cell at that point on the appropriate diagonal and summing them.

Next, the rows and columns:

// Rows
IntStream.range(0, n).forEach(y -> {
    if (IntStream.range(0, n).map(x -> getCell(x, y)).sum() != expectedValue) {
        throw new IllegalStateException("Row is not the expected value");
    }
});

// Cols
IntStream.range(0, n).forEach(x -> {
    if (IntStream.range(0, n).map(y -> getCell(x, y)).sum() != expectedValue) {
        throw new IllegalStateException("Column is not the expected value");
    }
});

Here we iterate over all the cells on each row or column as appropriate and sum up all of those values. If, in any of these cases, we get a different value from what we expected, then we’ll throw an exception, indicating that something is wrong.

4. Generating Magic Squares

At this point, we can correctly validate whether any given square is a magic square or not. So now we need to be able to generate them.

We saw earlier that there are three different algorithms to use here, depending on the size of the square. We’ll look at each in turn.

4.1. Algorithm for Odd-Sized Squares

The first algorithm we’ll look at is for squares with an odd number of cells on each side.

When generating a magic square of this size, we always start by putting the first number in the middle cell of the top row. We then proceed to place each subsequent number as follows:

• Firstly we attempt to place it in the cell immediately up and right from the previous square. When doing this, we wrap around at the edges, so, for example, after the top row, we’d move to the bottom row.
• If this desired cell is already populated, we instead place the next number in the cell immediately below the previous one. Again, when doing this, we wrap around at the edges.

For example, in our 3*3 square, we start in the top middle cell. We then move up and right, wrapping around to find the bottom right cell:

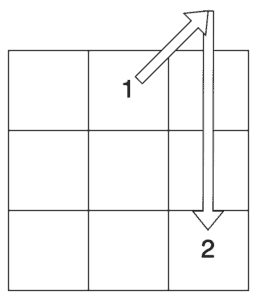
From here, we’d move up and right to populate the middle left cell. After this, moving up and right gets back to the first cell, so instead, we have to move down to the bottom left cell:

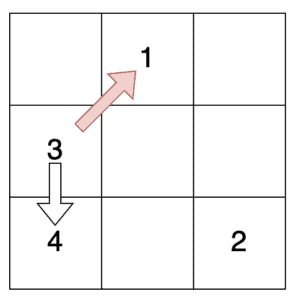
If we keep on doing this, we’ll eventually fill every square with a valid magic square.

4.2. Implementation for Odd-Sized Squares

So how do we do this in Java?

Firstly, let’s place our first number. This is in the center cell on the top row:

int y = 0;
int x = (n - 1) / 2;
setCell(x, y, 1);

Having done this, we’ll loop over all of the other numbers, placing each one in turn:

for (int number = 2; number <= n * n; ++number) {
    int nextX = ...;
    int nextY = ...;

    setCell(nextX, nextY, number);

    x = nextX;
    y = nextY;
}

Now we just need to determine what values to use for nextX and nextY.

To start with, we’ll attempt to move up and right, wrapping around as necessary:

int nextX = x + 1;
if (nextX == n) {
    nextX = 0;
}

int nextY = y - 1;
if (nextY == -1) {
    nextY = n - 1;
}

However, we also need to handle the case when this next cell is already occupied:

if (getCell(nextX, nextY) != 0) {
    nextX = x;

    nextY = y + 1;
    if (nextY == n) {
        nextY = 0;
    }
}

Putting all this together, we have our implementation to generate any odd-sized magic square. For example, a 9*9 square generated with this is:

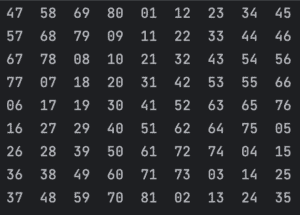
4.3. Algorithm for Doubly-Even Sized Squares

This above algorithm will work for odd-sized squares but not for even-sized squares. In fact, for those, we need one of two algorithms depending on the exact size.

Double-even squares are those where the sides are a multiple of 4 – e.g. 4*4, 8*8, 12*12, etc. In order to generate these, we need to separate out 4 special areas in our square. These areas are the cells that are n/4 from each edge whilst being more than n/4 from the corners:

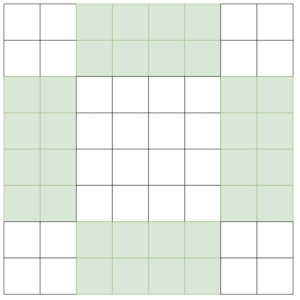
Having done this, we now fill in numbers. This is done in two passes. The first pass starts at the top left and works on rows from left to right. Every time we’re on an unhighlighted cell we add the next number in the sequence:

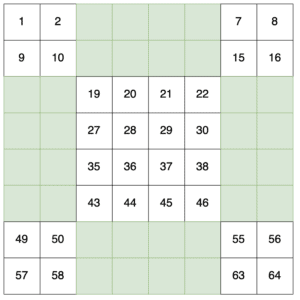
The second pass is exactly the same, but from the bottom right and running right to left, and adding numbers only to the highlighted cells:

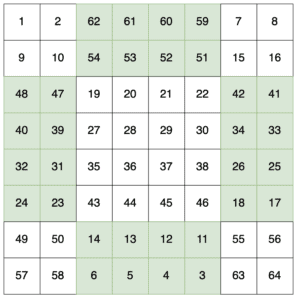
At this point, we’ve got our valid magic square.

4.4. Implementation for Doubly-Even Sized Squares

In order to implement this in Java, we need to make use of two techniques.

Firstly, we can actually add all of the numbers in a single pass. If we’re on an unhighlighted cell, then we do as before, but if we’re on a highlighted cell, then instead we’re counting down from n² instead:

int number = 1;

for (int y = 0; y < n; ++y) {
    for (int x = 0; x < n; ++x) {
        boolean highlighted = ...;
        
        if (highlighted) {
            setCell(x, y, (n * n) - number + 1);
        } else {
            setCell(x, y, number);
        }

        number += 1;
    }
}

Now we just need to work out what we consider our highlighted squares. We can do this by checking if our x and y coordinates are within range:

if ((y < n/4 || y >= 3*n/4) && (x >= n/4 && x < 3*n/4)) {
    highlighted = true;
} else if ((x < n/4 || x >= 3*n/4) && (y >= n/4 && y < 3*n/4)) {
    highlighted = true;
}

Our top condition is for the highlighted areas at the top and bottom of the square, whereas our second one is for the highlighted areas at the left and right of the square. We can see that they’re actually the same, only transposing x and y in the checks. In both cases, it’s where we’re within 1/4 of the square to that side and between 1/4 and 3/4 of the way from the adjacent corners.

Putting all this together, we have our implementation to generate any doubly-even-sized magic square. For example, our 8*8 square generated with this is:

4.5. Algorithm for Singly-Even Sized Squares

Our final size of squares is singly-even squares. That is, where the sides are divisible by 2 but not by 4. This also requires that the sides are at least 6 cells long – there are no solutions for a 2*2 magic square, so 6*6 is the smallest singly-even magic square that we can solve.

We start by first splitting them into quarters – each of which will be an odd-sized square. These are then populated using the same algorithm as for an odd-sized magic square, only assigning each quadrant a different range of numbers – starting with the top-left quarter, then the bottom-right, top-right, and finally the bottom-left:

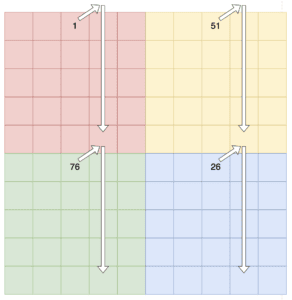
Once we’ve populated all of the squares using our odd-sized algorithm, we still don’t quite have a valid magic square. We’ll notice at this point that all of the columns add up to the correct number but that the rows and diagonals don’t. However, we’ll also notice that the rows in the top half all add up to the same number, and the rows in the second half also all add up to the same number:

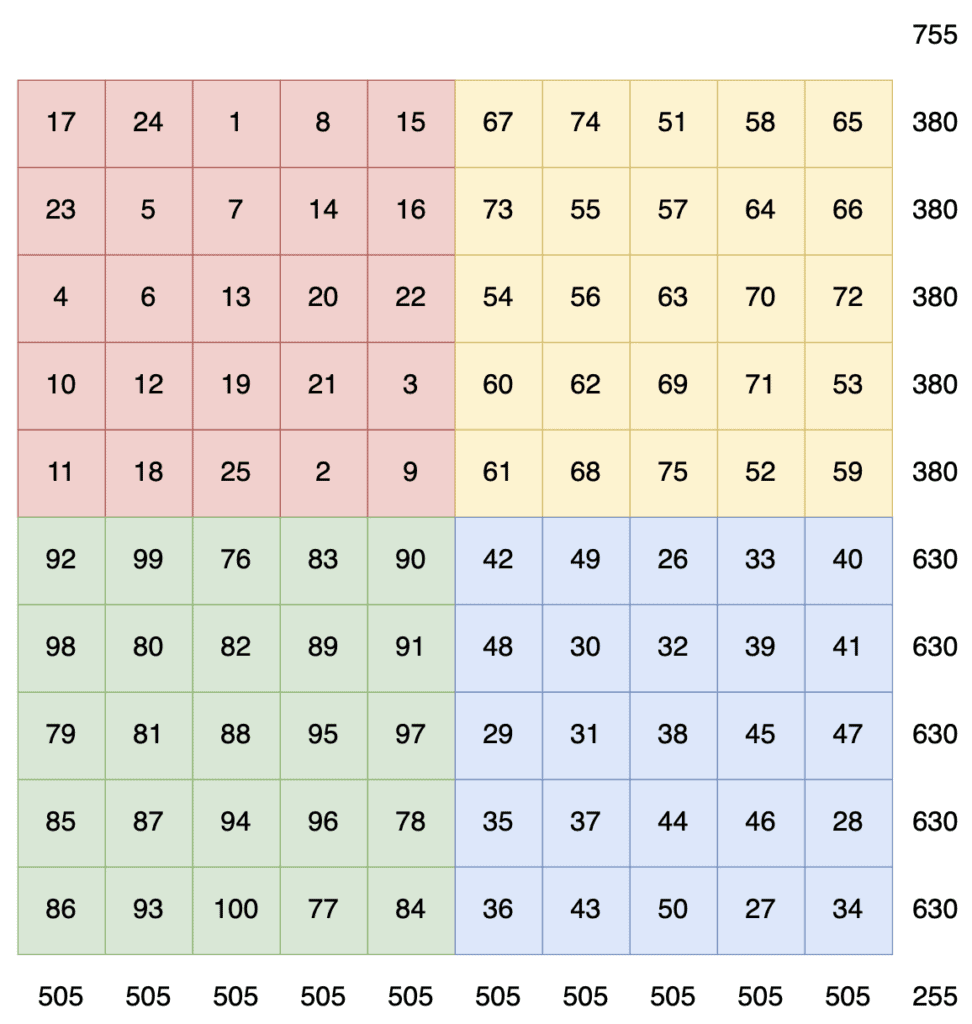
We can solve this by performing a number of swaps between the top and bottom halves, as follows:

• Every cell in the top row of our top-left quadrant that’s to the left of the center.
• Every cell in the bottom row of our top-left quadrant that’s to the left of the center.
• The same number of cells on each row between these, but starting one cell in.
• One less cell than these on each row in the top-right quadrant, but starting from the right-hand side.

This then looks as follows:

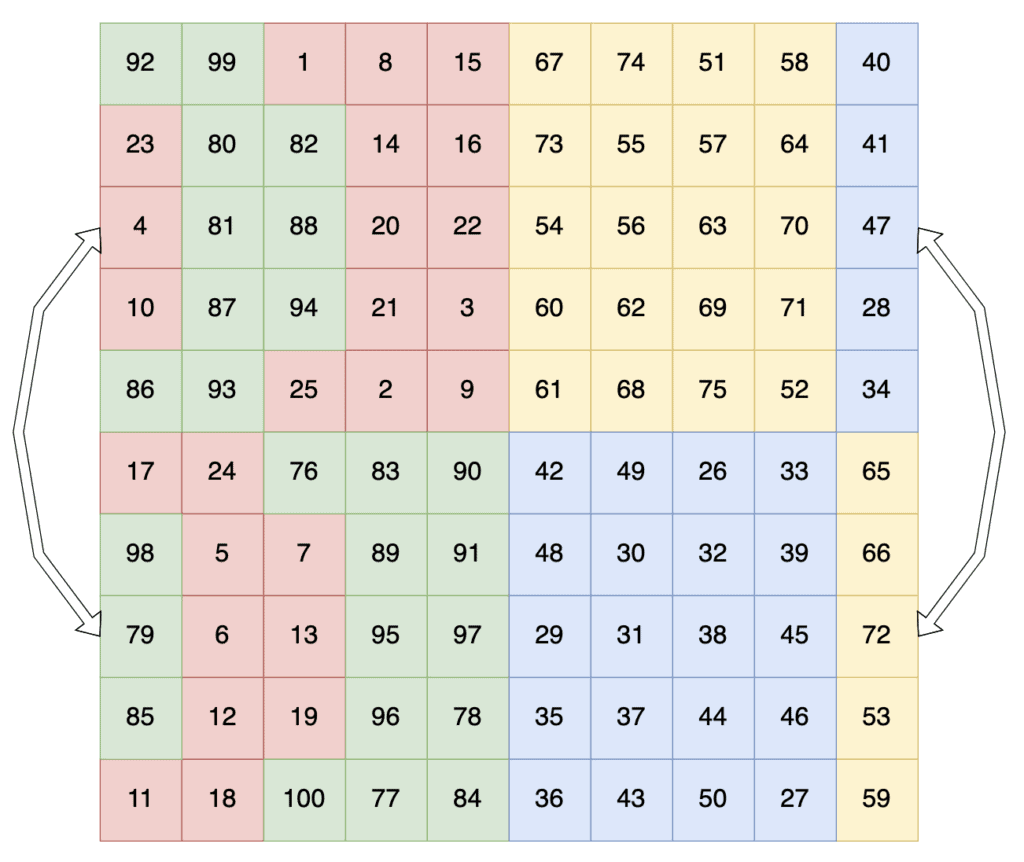
This is now a valid magic square, with every row, column, and diagonal adding up to the same value – 505 in this case.

4.6. Implementation for Singly-Even Sized Squares

The implementation for this will build off of what we did for odd-sized squares. Firstly we need to calculate some values to use for the generation:

int halfN = n/2;
int swapSize = n/4;

Note how we’re calculating our swapSize as being n/4 and then storing it into an int. This effectively rounds down, so for n=10, we’ll get a swapSize value of 2.

Next, we need to populate our grid. We’ll assume that we already have a function for performing the odd-sized square algorithm only offset as appropriately:

populateOddArea(0,     0,     halfN, 0);
populateOddArea(halfN, halfN, halfN, halfN * halfN);
populateOddArea(halfN, 0,     halfN, (halfN * halfN) * 2);
populateOddArea(0,     halfN, halfN, (halfN * halfN) * 3);

Now we’re left just needing to perform our swaps. Again, we’ll assume we have a function for swapping cells in our square.

Swapping the cells in the left quadrants is done just by iterating swapSize in from the left and performing the swaps:

for (int x = 0; x < swapSize; ++x) {
    swapCells(x, 0, x, halfN); // Top row
    swapCells(x, halfN - 1, x, n - 1); // Bottom row
    
    // All in-between rows.
    for (int y = 1; y < halfN - 1; ++y) {
        swapCells(x + 1, y, x + 1, y + halfN);
    }
}

Finally, we swap the cells in the right quadrant. This is done by iterating swapSize – 1 in from the right and performing the swaps:

for (int x = 0; x < swapSize - 1; ++x) {
    for (int y = 0; y < halfN; ++y) {
        swapCells(n - x - 1, y, n - x - 1, y + halfN);
    }
}

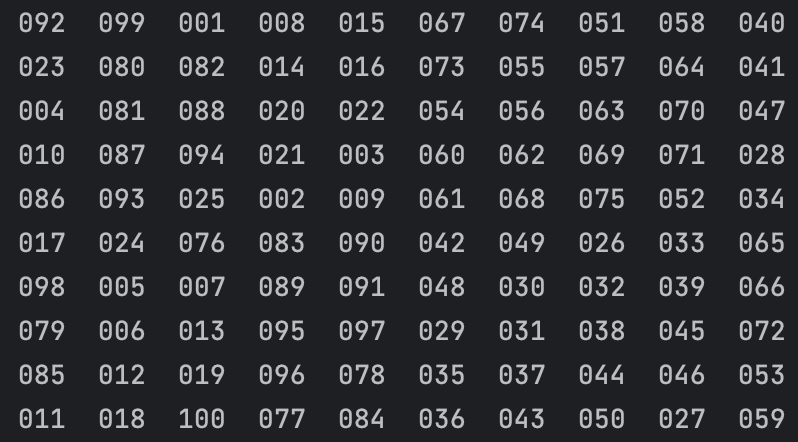
Putting all this together, we have our implementation to generate any singly-even-sized magic square. For example, our 10*10 square generated with this is as follows:

5. Summary

Here we’ve looked at the algorithms used to create magic squares and seen how we can implement these in Java.

As always, we can find all code from this article over on GitHub.