Find the Intersection of Two Lines in Java

Refactor Java code safely — and automatically — with OpenRewrite.

Refactoring big codebases by hand is slow, risky, and easy to put off. That’s where OpenRewrite comes in. The open-source framework for large-scale, automated code transformations helps teams modernize safely and consistently.

Each month, the creators and maintainers of OpenRewrite at Moderne run live, hands-on training sessions — one for newcomers and one for experienced users. You’ll see how recipes work, how to apply them across projects, and how to modernize code with confidence.

Join the next session, bring your questions, and learn how to automate the kind of work that usually eats your sprint time.

1. Overview

In this quick tutorial, we’ll show how to find the point of intersection of two lines defined by the linear functions in the slope-intercept form.

2. The Math Formula of Intersection

Any straight line (except vertical) on a plane can be defined by the linear function:

y = mx + b

where m is the slope and b is the y-intercept.

For a vertical line, m would be equal to infinity, that’s why we’re excluding it. If two lines are parallel, they have the same slope, that is the same value of m.

Let’s say we have two lines. The first function defines the first line:

y = m1x + b1

And the second function defines the second line:

y = m2x + b2

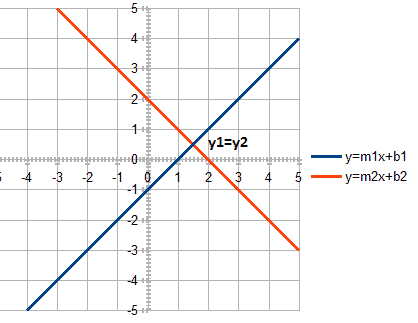
We want to find the point of intersection of these lines. Obviously, the equation is true for the point of intersection:

y1 = y2

Let’s substitute y-variables:

m1x + b1 = m2x + b2

From the above equation we can find the x-coordinate:

x(m1 - m2) = b2 - b1
x = (b2 - b1) / (m1 - m2)

Finally, we can find y-coordinate of the point of intersection:

y = m1x + b1

Let’s now move on to the implementation part.

3. Java Implementation

Firstly, we have four input variables – m1, b1 for the first line, and m2, b2 for the second line.

Secondly, we’ll convert the calculated point of intersection into the object of java.awt.Point type.

Finally, lines may be parallel, hence let’s make the returned value Optional<Point>:

public Optional<Point> calculateIntersectionPoint(
    double m1, 
    double b1, 
    double m2, 
    double b2) {

    if (m1 == m2) {
        return Optional.empty();
    }

    double x = (b2 - b1) / (m1 - m2);
    double y = m1 * x + b1;

    Point point = new Point();
    point.setLocation(x, y);
    return Optional.of(point);
}

Now let’s choose some values and test the method for parallel and non-parallel lines.

For example, let’s take the x-axis (y = 0) as the first line, and the line defined by y = x – 1 as the second line.

For the second line, the slope m is equal to 1 which means 45 degrees, and the y-intercept is equal to -1 which means that the line intercepts the y-axis in the point (0, -1).

It’s intuitively clear that the point of intersection of the second line with the x-axis must be (1,0):

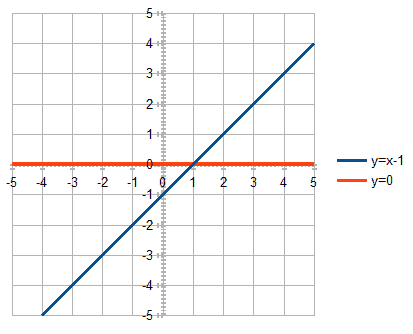
Let’s check it.

Firstly, let’s make sure that a Point is present, as the lines aren’t parallel, and then check the values of x and y:

@Test
public void givenNotParallelLines_whenCalculatePoint_thenPresent() {
    double m1 = 0;
    double b1 = 0;
    double m2 = 1;
    double b2 = -1;

    Optional<Point> point = service.calculateIntersectionPoint(m1, b1, m2, b2);

    assertTrue(point.isPresent());
    assertEquals(point.get().getX(), 1, 0.001);
    assertEquals(point.get().getY(), 0, 0.001);
}

Lastly, let’s take two parallel lines and make sure that the returned value is empty:

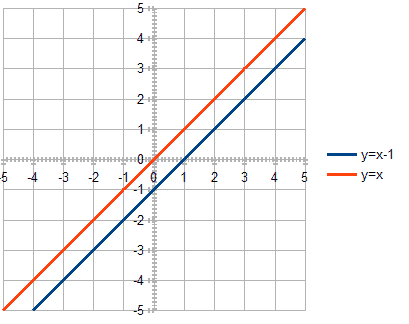
@Test
public void givenParallelLines_whenCalculatePoint_thenEmpty() {
    double m1 = 1;
    double b1 = 0;
    double m2 = 1;
    double b2 = -1;

    Optional<Point> point = service.calculateIntersectionPoint(m1, b1, m2, b2);

    assertFalse(point.isPresent());
}