1. Overview
In this quick tutorial, we’ll learn to solve an algorithmic problem of checking whether the two given rectangles overlap.
We’ll start by looking at the problem definition and then progressively build up a solution.
Finally, we’ll implement it in Java.
2. Problem Definition
Let’s say we have two given rectangles – r1 and r2. We need to check if there’s at least one common point between r1 and r2. If yes, it simply means that these two rectangles overlap.
Let’s have a look at some examples:
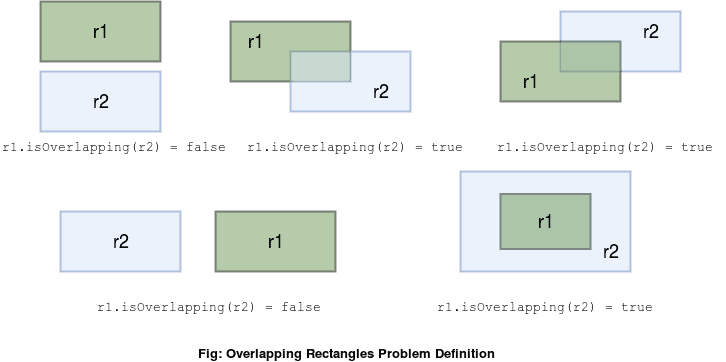
If we notice the very last case, the rectangles r1 and r2 have no intersecting boundaries. Still, they’re overlapping rectangles, as every point in r1 is also a point in r2.
3. Initial Setup
To solve this problem, we should first start by defining a rectangle programmatically. A rectangle can be easily represented by its bottom-left and top-right coordinates:
public class Rectangle {
private Point bottomLeft;
private Point topRight;
//constructor, getters and setters
boolean isOverlapping(Rectangle other) {
...
}
}
where Point is a class representing a point (x,y) in a two-dimensional space:
public class Point {
private int x;
private int y;
//constructor, getters and setters
}
We’ll later define the .isOverlapping() method in our Rectangle class to check if it overlaps with the compared rectangle.
4. Solution
The two given rectangles won’t overlap if either of the below conditions is true:
- One of the two rectangles is above the top edge of the other rectangle
- One of the two rectangles is on the left side of the left edge of the other rectangle
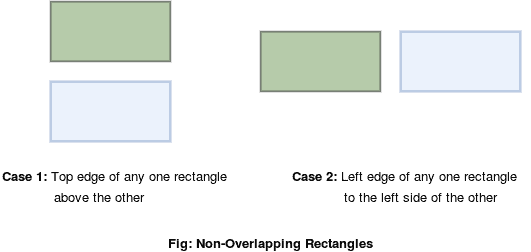
For all other cases, the two rectangles will overlap with each other. To convince ourselves, we can always draw out several examples.
5. Java Implementation
Now that we understand the solution, let’s implement our .isOverlapping() method:
public boolean isOverlapping(Rectangle comparedRectangle) {
if (this.topRight.getY() < comparedRectangle.bottomLeft.getY() || this.bottomLeft.getY() > comparedRectangle.topRight.getY()) {
return false;
}
if (this.topRight.getX() < comparedRectangle.bottomLeft.getX() || this.bottomLeft.getX() > comparedRectangle.topRight.getX()) {
return false;
}
return true;
}
Our .isOverlapping() method in the Rectangle class returns false if one of the rectangles is either above or to the left side of the other and true otherwise.
To find out if one rectangle is above the other, we compare their y-coordinates. Likewise, we compare the x-coordinates to check if one rectangle is to the left of the other.
5.1. Comparing Without Considering the Borders
Inside our problem statement, we didn’t define whether the border of the rectangle should be considered or not. The .isOverlapping() method considers the definition of the rectangle as closed intervals. Therefore, two touching rectangles are considered to overlap as they share at least one point of the border. Alternatively, we can define a new solution to ignore the borders and consider the Rectangles as open intervals:
public boolean isOverlappingWithoutBorders(Rectangle comparedRectangle) {
if (this.topRight.getY() <= comparedRectangle.bottomLeft.getY() || this.bottomLeft.getY() >= comparedRectangle.topRight.getY()) {
return false;
}
if (this.topRight.getX() <= comparedRectangle.bottomLeft.getX() || this.bottomLeft.getX() >= comparedRectangle.topRight.getX()) {
return false;
}
return true;
We can easily test both methods working as expected:
Rectangle rectangle1 = new Rectangle(new Point(0, 0), new Point(5, 14));
Rectangle rectangle2 = new Rectangle(new Point(5, 0), new Point(17, 14));
assertTrue(rectangle1.isOverlapping(rectangle2));
assertFalse(rectangle1.isOverlappingWithoutBorders(rectangle2));
Both methods work as expected.
6. Conclusion
In this short article, we learned how to solve an algorithmic problem of finding whether the two given rectangles overlap with each other, with and without borders. It serves as a collision detection strategy for two rectangular objects.
As usual, the entire source code is available over on Github.
