1. Overview
In this tutorial, we’re going to see how we can use BitSets to represent a vector of bits.
First, we’ll start with the rationale behind not using the boolean[]. Then after getting familiar with the BitSet internals, we’ll take a closer look at its API.
2. Array of Bits
To store and manipulate arrays of bits, one might argue that we should use boolean[] as our data structure. At first glance, that might seem a reasonable suggestion.
However, each boolean member in a boolean[] usually consumes one byte instead of just one bit. So when we have tight memory requirements, or we’re just aiming for a reduced memory footprint, boolean[] are far from being ideal.
To make matters more concrete, let’s see how much space a boolean[] with 1024 elements consumes:
boolean[] bits = new boolean[1024];
System.out.println(ClassLayout.parseInstance(bits).toPrintable());
Ideally, we expect a 1024-bit memory footprint from this array. However, the Java Object Layout (JOL) reveals an entirely different reality:
[Z object internals:
OFFSET SIZE TYPE DESCRIPTION VALUE
0 4 (object header) 01 00 00 00 (00000001 00000000 00000000 00000000) (1)
4 4 (object header) 00 00 00 00 (00000000 00000000 00000000 00000000) (0)
8 4 (object header) 7b 12 07 00 (01111011 00010010 00000111 00000000) (463483)
12 4 (object header) 00 04 00 00 (00000000 00000100 00000000 00000000) (1024)
16 1024 boolean [Z. N/A
Instance size: 1040 bytes
If we ignore the overhead of object header, the array elements are consuming 1024 bytes, instead of the expected 1024 bits. That’s 700% more memory than what we expected.
The addressability issues and word tearing are the main reasons why booleans are more than just one single bit.
To solve this problem, we can use a combination of numeric data types (such as long) and bit-wise operations. That’s where the BitSet comes in.
3. How BitSet Works
As we mentioned earlier, to achieve the one bit per flag memory usage, the BitSet API uses a combination of basic numeric data types and bit-wise operations.
For the sake of simplicity, let’s suppose we’re going to represent eight flags with one byte. At first, we initialize all bits of this single byte with zero:

Now if we want to set the bit at position three to true, we should first left-shift the number 1 by three:
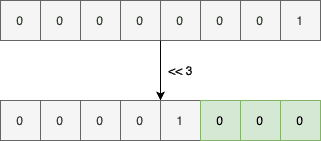
And then or its result with the current byte value:
The same process will happen if decide to set the bit at the index seven:
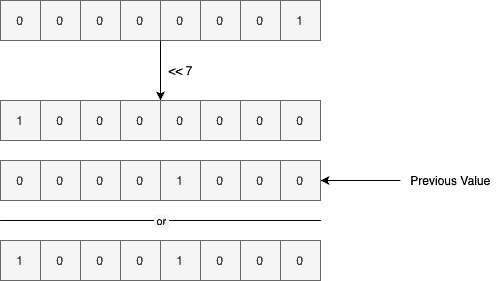
As shown above, we perform a left-shift by seven bits and combine the result with the previous byte value using the or operator.
3.1. Getting a Bit Index
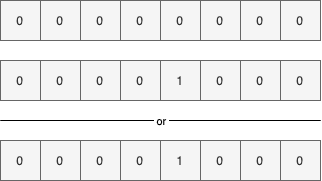
To check if a particular bit index is set to true or not, we’ll use the and operator. For instance, here’s how we check if index three is set:
- Performing a left-shift by three bits on the value one
- Anding the result with the current byte value
- If the result is greater than zero, then we found a match, and that bit index is actually set. Otherwise, the requested index is clear or is equal to false

The above diagram shows the get operation steps for index three. If we inquire about a clear index, however, the result will be different:

Since the and result is equal to zero, index four is clear.
3.2. Growing the Storage
Currently, we can only store a vector of 8 bits. To go beyond this limitation, we just have to use an array of bytes, instead of a single byte, that’s it!
Now, every time we need to set, get, or clear a specific index, we should find the corresponding array element, first. For instance, let’s suppose we’re going to set index 14:

As shown in the above diagram, after finding the right array element, we did set the appropriate index.
Also, if we want to set an index beyond 15 here, the BitSet will expand its internal array, first. Only after expanding the array and copying the elements will it set the requested bit. This is somewhat similar to how ArrayList works internally.
So far, we used the byte data type for the sake of simplicity. The BitSet API, however, is using an array of long values internally.
4. The BitSet API
Now that we know enough about the theory, it’s time to see what the BitSet API looks like.
For starters, let’s compare the memory footprint of a BitSet instance with 1024 bits with the boolean[] we saw earlier:
BitSet bitSet = new BitSet(1024);
System.out.println(GraphLayout.parseInstance(bitSet).toPrintable());
This will print both the shallow size of the BitSet instance and the size of its internal array:
java.util.BitSet@75412c2fd object externals:
ADDRESS SIZE TYPE PATH VALUE
70f97d208 24 java.util.BitSet (object)
70f97d220 144 [J .words [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
As shown above, it uses a long[] with 16 elements (16 * 64 bits = 1024 bits) internally. Anyway, this instance is using 168 bytes in total, while the boolean[] were using 1024 bytes.
The more bits we have, the more the footprint difference increases. For example, to store 1024 * 1024 bits, the boolean[] consumes 1 MB, and the BitSet instance consumes around 130 KB.
4.1. Constructing BitSets
The simplest way to create a BitSet instance is to use the no-arg constructor:
BitSet bitSet = new BitSet();
This will create a BitSet instance with a long[] of size one. Of course, it can automatically grow this array if needed.
It’s also possible to create a BitSet with an initial number of bits:
BitSet bitSet = new BitSet(100_000);
Here, the internal array will have enough elements to hold 100,000 bits. This constructor comes in handy when we already have a reasonable estimate on the number of bits to store. In such use cases, it can prevent or decrease the unnecessary copying of array elements while growing it.
It’s even possible to create a BitSet from an existing long[], byte[], LongBuffer, and ByteBuffer. For instance, here we’re creating a BitSet instance from a given long[]:
BitSet bitSet = BitSet.valueOf(new long[] { 42, 12 });
There are three more overloaded versions of the valueOf() static factory method to support the other mentioned types.
4.2. Setting Bits
We can set the value of a particular index to true using the set(index) method:
BitSet bitSet = new BitSet();
bitSet.set(10);
assertThat(bitSet.get(10)).isTrue();
As usual, the indices are zero-based. It’s even possible to set a range of bits to true using the set(fromInclusive, toExclusive) method:
bitSet.set(20, 30);
for (int i = 20; i <= 29; i++) {
assertThat(bitSet.get(i)).isTrue();
}
assertThat(bitSet.get(30)).isFalse();
As is evident from the method signature, the beginning index is inclusive, and the ending one is exclusive.
When we say setting an index, we usually mean setting it to true. Despite this terminology, we can set a particular bit index to false using the set(index, boolean) method:
bitSet.set(10, false);
assertThat(bitSet.get(10)).isFalse();
This version also supports setting a range of values:
bitSet.set(20, 30, false);
for (int i = 20; i <= 29; i++) {
assertThat(bitSet.get(i)).isFalse();
}
4.3. Clearing Bits
Instead of setting a specific bit index to false, we can simply clear it using the clear(index) method:
bitSet.set(42);
assertThat(bitSet.get(42)).isTrue();
bitSet.clear(42);
assertThat(bitSet.get(42)).isFalse();
Moreover, we can also clear a range of bits with the clear(fromInclusive, toExclusive) overloaded version:
bitSet.set(10, 20);
for (int i = 10; i < 20; i++) {
assertThat(bitSet.get(i)).isTrue();
}
bitSet.clear(10, 20);
for (int i = 10; i < 20; i++) {
assertThat(bitSet.get(i)).isFalse();
}
Interestingly, if we call this method without passing any arguments, it’ll clear all the set bits:
bitSet.set(10, 20);
bitSet.clear();
for (int i = 0; i < 100; i++) {
assertThat(bitSet.get(i)).isFalse();
}
As shown above, after calling the clear() method, all bits are set to zero.
4.4. Getting Bits
So far, we used the get(index) method quite extensively. When the requested bit index is set, then this method will return true. Otherwise, it’ll return false:
bitSet.set(42);
assertThat(bitSet.get(42)).isTrue();
assertThat(bitSet.get(43)).isFalse();
Similar to set and clear, we can get a range of bit indices using the get(fromInclusive, toExclusive) method:
bitSet.set(10, 20);
BitSet newBitSet = bitSet.get(10, 20);
for (int i = 0; i < 10; i++) {
assertThat(newBitSet.get(i)).isTrue();
}
As shown above, this method returns another BitSet in the [20, 30) range of the current one. That is, index 20 of the bitSet variable is equivalent to index zero of the newBitSet variable.
4.5. Flipping Bits
To negate the current bit index value, we can use the flip(index) method. That is, it’ll turn true values to false and vice versa:
bitSet.set(42);
bitSet.flip(42);
assertThat(bitSet.get(42)).isFalse();
bitSet.flip(12);
assertThat(bitSet.get(12)).isTrue();
Similarly, we can achieve the same thing for a range of values using the flip(fromInclusive, toExclusive) method:
bitSet.flip(30, 40);
for (int i = 30; i < 40; i++) {
assertThat(bitSet.get(i)).isTrue();
}
4.6. Length
There are three length-like methods for a BitSet. The size() method returns the number of bits the internal array can represent. For instance, since the no-arg constructor allocates a long[] array with one element, then the size() will return 64 for it:
BitSet defaultBitSet = new BitSet();
assertThat(defaultBitSet.size()).isEqualTo(64);
With one 64-bit number, we can only represent 64 bits. Of course, this will change if we pass the number of bits explicitly:
BitSet bitSet = new BitSet(1024);
assertThat(bitSet.size()).isEqualTo(1024);
Moreover, the cardinality() method represents the number of set bits in a BitSet:
assertThat(bitSet.cardinality()).isEqualTo(0);
bitSet.set(10, 30);
assertThat(bitSet.cardinality()).isEqualTo(30 - 10);
At first, this method returns zero as all bits are false. After setting the [10, 30) range to true, then the cardinality() method call returns 20.
Also, the length() method returns the one index after the index of the last set bit:
assertThat(bitSet.length()).isEqualTo(30);
bitSet.set(100);
assertThat(bitSet.length()).isEqualTo(101);
At first, the last set index is 29, so this method returns 30. When we set the index 100 to true, then the length() method returns 101. It’s also worth mentioning that this method will return zero if all bits are clear.
Finally, the isEmpty() method returns false when there is at least one set bit in the BitSet. Otherwise, it’ll return true:
assertThat(bitSet.isEmpty()).isFalse();
bitSet.clear();
assertThat(bitSet.isEmpty()).isTrue();
4.7. Combining With Other BitSets
The intersects(BitSet) method takes another BitSet and returns true when two BitSets have something in common. That is, they have at least one set bit in the same index:
BitSet first = new BitSet();
first.set(5, 10);
BitSet second = new BitSet();
second.set(7, 15);
assertThat(first.intersects(second)).isTrue();
The [7, 9] range is set in both BitSets, so this method returns true.
It’s also possible to perform the logical and operation on two BitSets:
first.and(second);
assertThat(first.get(7)).isTrue();
assertThat(first.get(8)).isTrue();
assertThat(first.get(9)).isTrue();
assertThat(first.get(10)).isFalse();
This will perform a logical and between the two BitSets and modifies the first variable with the result. Similarly, we can perform a logical xor on two BitSets, too:
first.clear();
first.set(5, 10);
first.xor(second);
for (int i = 5; i < 7; i++) {
assertThat(first.get(i)).isTrue();
}
for (int i = 10; i < 15; i++) {
assertThat(first.get(i)).isTrue();
}
There are other methods such as the andNot(BitSet) or the or(BitSet), which can perform other logical operations on two BitSets.
4.8. Miscellaneous
As of Java 8, there is a stream() method to stream all set bits of a BitSet. For instance:
BitSet bitSet = new BitSet();
bitSet.set(15, 25);
bitSet.stream().forEach(System.out::println);
This will print all set bits to the console. Since this will return an IntStream, we can perform common numerical operations such as summation, average, counting, and so on. For instance, here we’re counting the number of set bits:
assertThat(bitSet.stream().count()).isEqualTo(10);
Also, the nextSetBit(fromIndex) method will return the next set bit index starting from the fromIndex:
assertThat(bitSet.nextSetBit(13)).isEqualTo(15);
The fromIndex itself is included in this calculation. When there isn’t any true bit left in the BitSet, it’ll return -1:
assertThat(bitSet.nextSetBit(25)).isEqualTo(-1);
Similarly, the nextClearBit(fromIndex) returns the next clear index starting from the fromIndex:
assertThat(bitSet.nextClearBit(23)).isEqualTo(25);
On the other hand, the previousClearBit(fromIndex) returns the index of the nearest clear index in the opposite direction:
assertThat(bitSet.previousClearBit(24)).isEqualTo(14);
Same is true for previousSetBit(fromIndex):
assertThat(bitSet.previousSetBit(29)).isEqualTo(24);
assertThat(bitSet.previousSetBit(14)).isEqualTo(-1);
Moreover, we can convert a BitSet to a byte[] or a long[] using the toByteArray() or toLongArray() methods, respectively:
byte[] bytes = bitSet.toByteArray();
long[] longs = bitSet.toLongArray();
5. Conclusion
In this tutorial, we saw how we can use BitSets to represent a vector of bits.
At first, we got familiar with the rationale behind not using boolean[] to represent a vector of bits. Then we saw how a BitSet works internally and what its API looks like.
The code backing this article is available on GitHub. Once you're
logged in as a Baeldung Pro Member, start learning and coding on the project.
























