What Is the Riemann Zeta Function? | Baeldung on Computer Science

1. Overview

The Riemann zeta function, also called the Euler-Riemann zeta function, is one of mathematics’s most significant and intriguing functions. It was first defined for real numbers by Leonhard Euler. The German mathematician Bernhard Riemann extended the Euler definition to a complex variable in his On the Number of Primes Less Than a Given Magnitude.

The Riemann zeta function has played a crucial role in various areas of mathematics, particularly number theory, complex analysis, and physics.

In this tutorial, we’ll delve into its fundamentals and explore its fascinating connection with prime numbers.

2. Definition

The Riemann zeta function, denoted by $\zeta(s)$ , is defined as:

(1) $\begin{equation*} \zeta(s)=1^s+2^s+3^s+4^s+\ldots=\sum_{n=1}^{\infty} \frac{1}{n^s} \end{equation*}$

where $s$ is a complex variable with a real part greater than 1, i.e. $\operatorname{Re}(s)>1$ .
For $s=1$ it reduces to the harmonic series, which diverges. The Riemann zeta function converges absolutely for all complex numbers $s$ with a real part greater than 1. In this case, the function can be written as a convergent integral:

(2) $\begin{equation*} \zeta(s)=\sum_{n=1}^{\infty} \frac{1}{n^s}=\frac{1}{\Gamma(s)} \int_0^{\infty} \frac{x^{s-1}}{e^x-1} \mathrm{~d} x \end{equation*}$

where

(3) $\begin{equation*} \Gamma(s)=\int_0^{\infty} x^{s-1} e^{-x} \mathrm{~d} x . \end{equation*}$

is the Gamma function. One remarkable property of the Riemann zeta function is its ability to be analytically continued to the entire complex plane, except for a simple pole at $s = 1$ . This means that the function can be extended beyond its original domain of convergence while preserving certain properties.

2. The Functional Equation

The Riemann zeta function satisfies a functional equation relating its values at $s$ and $1 - s$ :

(4) $\begin{equation*} \zeta(s)=2^s \pi^{s-1} \sin \left(\frac{\pi s}{2}\right) \Gamma(1-s) \zeta(1-s) \end{equation*}$

The equation connects values of the Riemann zeta function at s and 1 − s, particularly relating even positive integers with odd negative integers.

Due to the zeros of the sine function, the functional equation suggests that $\zeta(s)$ has a simple zero at each even negative integer s = −2n. Hence the values $\mathbf{s=-2}$ , $\mathbf{s=-4}$ , $\mathbf{s=-6}$ , etc. are known as trivial zeros of $\mathbf{\zeta(s)}$ . Conversely, the even positive integer $s=+2$ , $s=+4$ , $s=+6$ , etc., are not zeros of $\zeta(s)$ because the term $\Gamma(1-s)$ has simple poles at the values -1, -3, -5 that overrides the zeros of the sine factor.

3. The Riemann Hypothesis

The Riemann hypothesis is one of the most famous unsolved problems in mathematics. It asserts that all non-trivial zeros of the Riemann zeta function lie on the line $\operatorname{Re}(s) = \frac{1}{2}$ of the complex plane. In other words, if $\zeta(s) = 0$ and $s$ is not a negative even integer, then the real part of $s$ is $1/2$ . The truth of this conjecture has profound implications for the distribution of prime numbers and has motivated extensive research over the past century.

It can be demonstrated that all non-trivial zeros of the Riemann function lie in the strip $0 < \operatorname{Re}(s) < 1$ , which is called the critical strip. Conversely, the set of points with $\operatorname{Re}(s) = \frac{1}{2}$ is called critical line. The proof that the non-trivial zeros lie on the critical line is still missing. Conrey demonstrated in 1989 that over than 40% of the non-trivial zeros of $\zeta(s)$ lie on the critical line.

The following figure represents the zeros of $\zeta$ visualized in the complex plane:

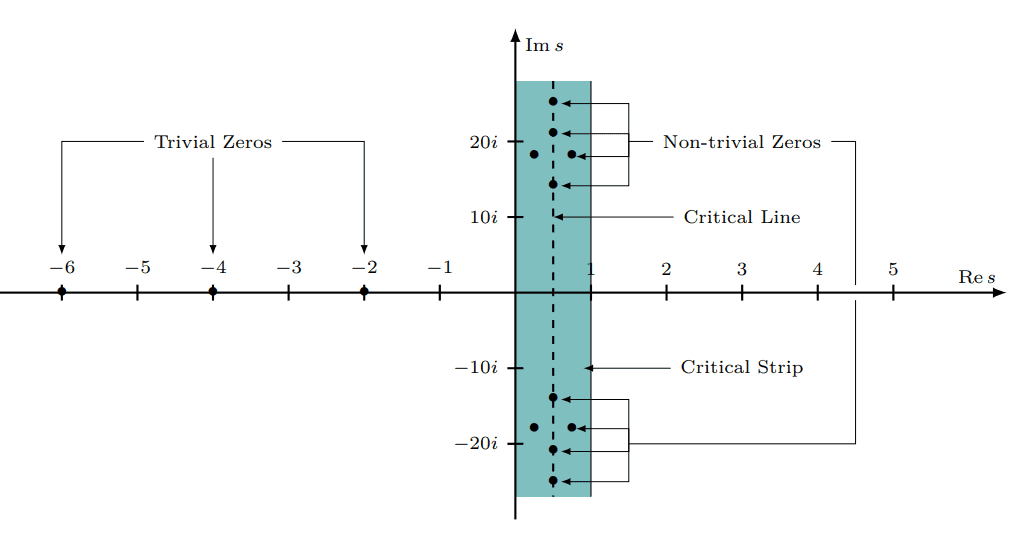
The zeros in the critical line are true zeros. Conversely, the zeros outside the critical line but within the critical strip are not true zeros. However, theoretical zeros within the critical strip with a real part different from 1/2 are possible. If one can identify such zeros, then it would disprove the Riemann hypothesis.

4. Relationship With Prime Numbers

4.1. The Euler Product Formula

Euler discovered in 1737 the first connection between the zeta function and prime numbers. He demonstrated the following identity:

(5) $\begin{equation*} \sum_{n=1}^{\infty} \frac{1}{n^s}=\prod_{p \text { prime }} \frac{1}{1-p^{-s}} \end{equation*}$

the zeta function appears on the left side, and on the right side, there is an infinite product extended over all prime numbers.
Hence, the zeta function is strictly related to prime numbers because it is given by an infinite product of factors containing prime numbers:

(6) $\begin{equation*} \zeta (s) =\frac{1}{1-2^{-s}} \cdot \frac{1}{1-3^{-s}} \cdot \frac{1}{1-5^{-s}} \cdot \frac{1}{1-7^{-s}} \cdot \frac{1}{1-11^{-s}} \cdots \frac{1}{1-p^{-s}} \cdots \end{equation*}$

For $s=1$ the zeta function corresponds to the harmonic series, which diverges. This observation proves Euclid’s theorem, which states that there are infinitely many prime numbers.

4.2. The Prime Counting Function

The prime counting function, denoted as $\mathbf{\Pi(x)}$ , returns the number of prime numbers less than or equal to a given real number $\mathbf{x}$ . In other words, it represents the cumulative distribution function of prime numbers.

For example:

$\Pi(10)=4$ , because there are 4 prime numbers (2, 3, 5, 7) less than or equal to 10
$\Pi(20)=8$ , because there are 8 prime numbers (2, 3, 5, 7, 11, 13, 17, 19) less than or equal to 20

The prime counting function is a fundamental concept in number theory, and it has been a subject of intense study.
For $x>1$ , let’s define $\Pi_0(x) = \Pi(x) - \frac{1}{2}$ if $x$ is a prime number, and $\Pi_0(x) = \Pi(x)$ otherwise. Rieman, in his paper “On the Number of Primes Less Than a Given Magnitude”, demonstrated the following identity:

(7) $\begin{equation*} \pi_0(x) = \mathrm{R}(x)-\sum_\rho \mathrm{R}\left(x^\rho\right)-\frac{1}{\log (x)}+\frac{1}{\pi} \arctan \frac{\pi}{\log (x)} \end{equation*}$

where

(8) $\begin{equation*} \mathrm{R}(x)=\sum_{n=1}^{\infty} \frac{\mu(n)}{n} \mathrm{li}\left(x^{1 / n}\right) \end{equation*}$

$\mathrm{li}(x)$ is the logarithmic integral function, $\mu(n)$ represents the Möbius function and the $\rho$ indexes represent the non-trivial zeros of the Rieman zeta function.

In the following animation, we show the prime counting function and its approximation obtained by summing the terms associated with the first 200 non-trivial zeros of the zeta function:

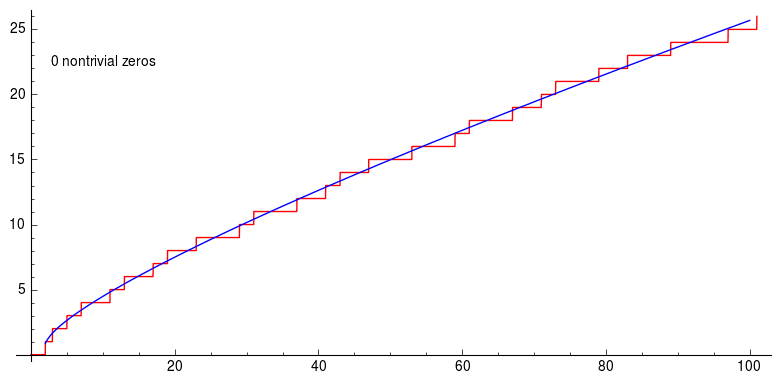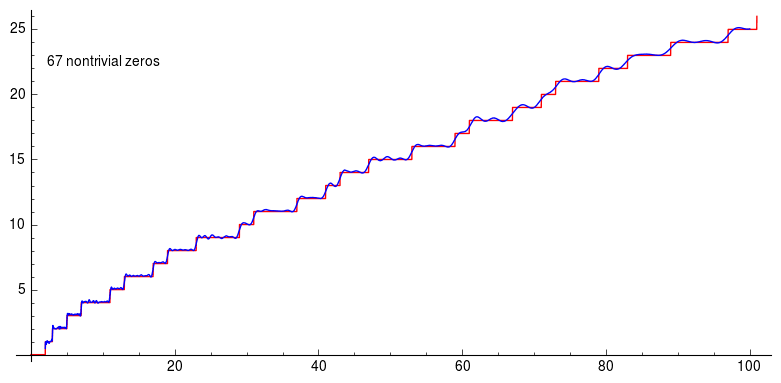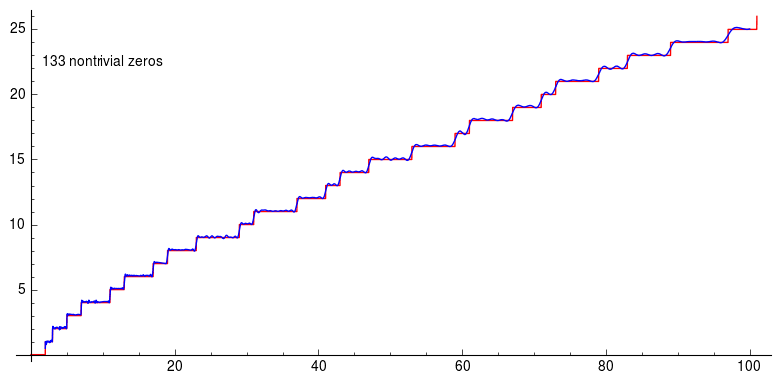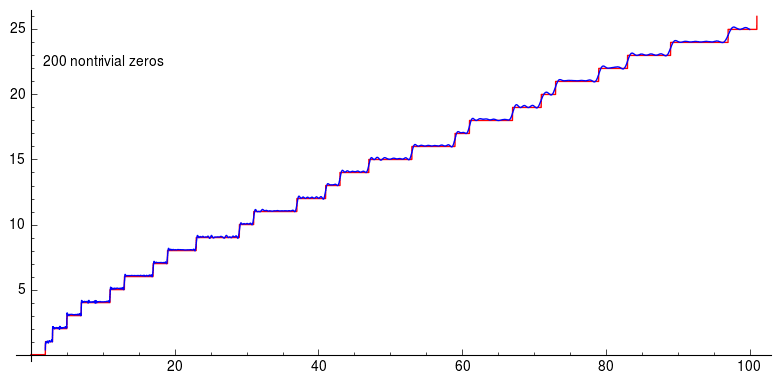
5. Conclusion

In this article, we reviewed the Zeta Riemann function, a fundamental mathematics study object. First, we explained the definition and properties of the function. Finally, we discussed the Riemann Hypothesis and the profound connection of the Zeta function with prime numbers.

Despite its profound significance, many mysteries surrounding the Riemann zeta function remain unsolved, making it a subject of ongoing research and fascination for mathematicians around the world.

Core Concepts

Operating Systems

Artificial Intelligence

Graph Theory

Latex

Full Archive

About Baeldung