1. Introduction
There are many algorithms to sort data. Usually, when we choose a sorting algorithm, we rely on criteria such as speed and space usage.
In this tutorial, we’ll be comparing two popular sorting algorithms Quicksort and Mergesort. Both algorithms apply the divide-and-conquer approach in different ways and also different properties when it comes to performance and storage use.
2. Quicksort
Quicksort is a popular in-place sorting algorithm that applies the divide-and-conquer approach. We can summarise quick sort into three main steps:
- Pick an element as a pivot
- Partition the problem set by moving smaller elements to the left of the pivot and larger elements to its right
- Repeat the above steps on each partition until we reach a sorted list
Let’s go through a small example where we sort the following list using Quicksort:

The first step is we pick a pivot. There are different ways to pick a pivot, but for this example, we will be choosing the right-most element always.
Once we have picked out pivot 23, we need to move all elements greater than 23 to its right and all elements smaller than 23 to its left. Remember, we are not worried about the order at this stage. We’re just positioning the elements in relation to the pivot.
By doing this, we’ve divided our list into two partitions:

Now we can repeat the steps of the algorithm over each of the partitions. Since the right-most partition only consists of one element, we can apply the steps over the left-most partition [15, 3, 8, 10. 5] by choosing 5 as the pivot then organizing the elements around it. Notice after we do this how we are slowly getting closer to a sorted set:

Now we have two partitions around [5] which are [3], which doesn’t need any further partitioning, and [15,8,10]. By picking 10 as the pivot and organizing the remaining 15 and 8 around it, we reach our final sorted list:

For a more in-depth explanation of Quicksort and the different ways we can choose our pivot, we can read an overview article of Quicksort.
Next, let’s apply Mergesort to the same array and see how it works.
3. Mergesort
Mergesort is another divide-and-conquer algorithm. However, unlike Quicksort, it is not an in-place algorithm and requires temporary arrays to store the sorted sub-arrays.
We can summarise mergesort into two main steps:
- Divide the list into sub-lists until we reach one element
- Merge sub-lists into sorted sub-lists repeatedly until we reach the final sorted list
Let’s now apply the concepts to the same array we used in our previous example. Starting with the unsorted list, we divide the list into its smallest sub-lists:

Now we’ll take each two sub-lists and merge them together, making sure that the merged sublist is sorted. We now have four sorted sub-lists:
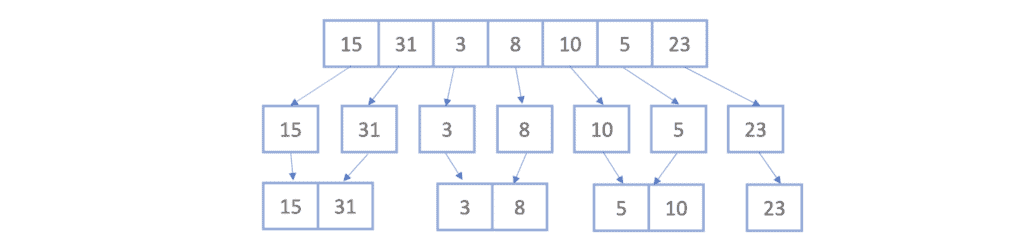
Again, we’ll take each two sub-lists and merge them together into sorted sub-lists which gives us two sorted sub-lists :
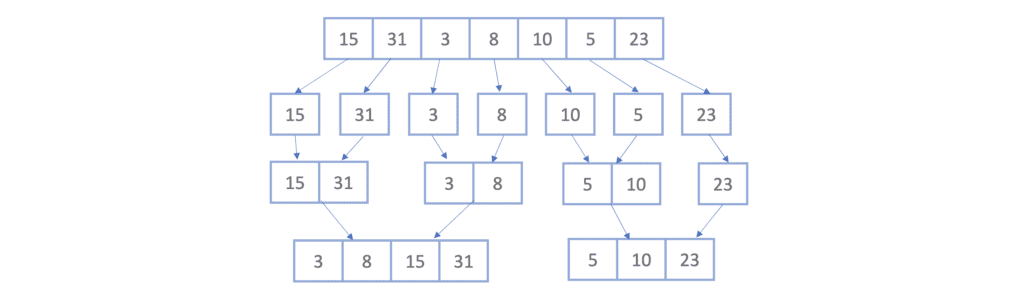
Finally, we apply the same concept one last time, which will give us the final sorted list:
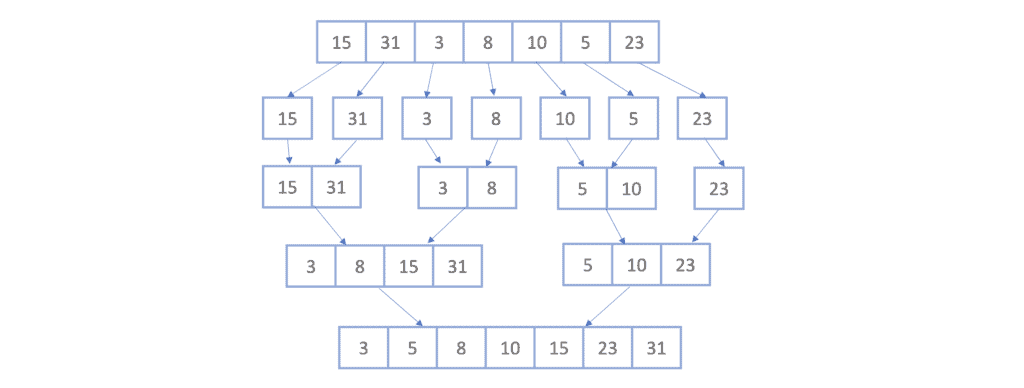
For a more in-depth overview of the mergesort algorithm and how it is implemented, we can see this article which explains how merge sort is applied on a linked list.
4. Comparing Between Mergesort and Quicksort
Now that we have an idea of how Quicksort and Mergesort work, let’s see the main differences between these two algorithms:
5. Conclusion
In this article, we discussed two sorting algorithms: Quicksort and Mergesort.
We learned how these methods worked in action and compared them in terms of space, and time complexity, and other properties such as stability and in-place sorting.