Why Can’t Prim’s or Kruskal’s Algorithms Be Used on a Directed Graph?

1. Introduction

In this tutorial, we’re going to explore why we can’t use Prim‘s and Kruskal‘s algorithms on a directed graph.

2. Minimum Span Tree

Both algorithms are used to find a minimum spanning tree in an undirected graph. A minimum spanning tree (MST) is a subgraph of a graph. This subgraph contains the edges with the fewest weight and at the same time all nodes from the original graph:

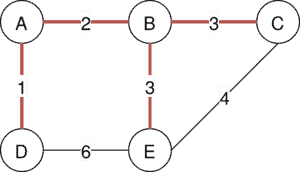
The shown graph visualizes the minimum span tree with a weight of 9.

2.1. Kruskal’s Algorithm

For Kruskal’s algorithm to work, we need a graph that is undirected, weighted, and connected. Its idea is quite simple:

Create a data structure $S$ .
Add the edge with the lowest weight, such that the graph created by it does not contain a circuit, to the data structure $S$ .
Continue these steps until $S$ forms a spanning tree.

Here we can already notice that we might encounter a problem if we do not detect the circle correctly, as in directed graphs.

2.2. Prim’s Algorithm

Prim’s algorithm works by starting at a random node and traversing the graph selecting the edge with the lowest weight. While this method reminds us of Dijkstra’s algorithm it actually only prioritizes the edges’ direct weight and not the whole path to the starting node such as with Dijkstra.

For a closer view, we take a look at the pseudo-code:

algorithm PrimsAlgorithm:
    // INPUT
    //    G = an undirected, weighted, and connected graph
    // OUTPUT
    //    T = the minimal spanning tree of G
    T <- create an empty tree
    Set a random node r as the root of T

    Q <- initialize a priority queue

    // Let cost(u) be the distance of node u to T
    // Initially, cost(u) = weight(u, r) for u in the neighbors of r
    // and cost(u) = infinity for every other node.

    Insert the nodes of G into Q except the root
    
    while Q is not empty:
        u <- pop from Q the closest node to T (not already in T)
        Add the corresponding edge to T
        for v in the neighbors of u:
            if v not in T and weight(u, v) < cost(v):
                cost(v) <- weight(u, v)

2.3. Comparsion

To quickly compare the two algorithms we conclude that Kruskal’s algorithm works very well on a sparse graph and is easy to implement. Prim’s algorithm on the other hand is faster for graphs with a lot of edges but it is also harder to implement.

3. Problem Instances

As we have already seen in the analysis of the algorithms, both of them require an undirected graph. While inputting a directed graph does not automatically stop the algorithm, a few examples can show why we can not allow directed graphs per se.

3.1. The Arborescence Problem

Since we do not have the classical concept of a minimum spanning tree in a directed graph we will work with the minimum spanning arborescence (MSA). The minimum spanning arborescence is a directed tree. It contains one node from which there exists a path to every other node in the graph:

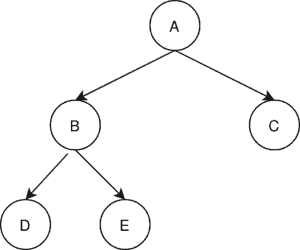
3.1. Kruskal

A counterexample for the Kruskal algorithm:

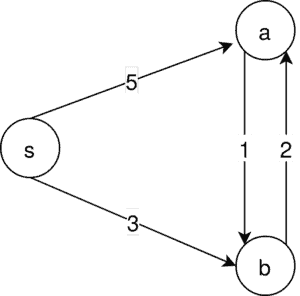
In our example, there is just one MSA possible. That is $s \rightarrow b \rightarrow a$ . But running Kruskal’s algorithm, we first of all select $a \rightarrow b$ :

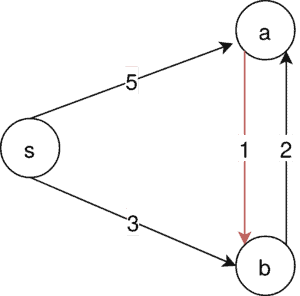
Since this edge is not contained in our MSA it is impossible to construct one from the Kruskal algorithm in this example.

3.2. Prim

For the Prim algorithm, we have a similar setup:

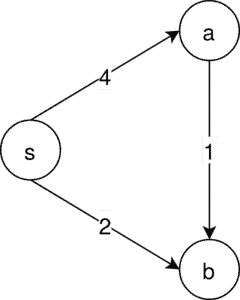
This time the only possible MSA is $s \rightarrow a \rightarrow b$ . Prim’s algorithm starts at a random node, in this case, $s$ . It then takes the edge with the lowest edge connected to $s$ , which is the node to $b$ :

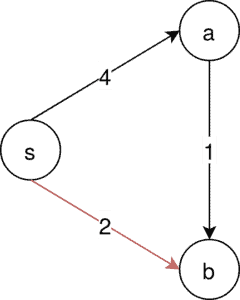
Since the edge, $s \rightarrow b$ is not contained in the only MSA that the following steps won’t generate an MSA for this example.

4. Chu–Liu/Edmonds’ Algorithm

Chiu-Liu/Edmonds’ algorithm is an alternative capable of solving the MSA problem for directed, connected graphs. For it to work we need an already chosen node r, which acts as the root for our MSA. The algorithm transforms our graph recursively into an MSA by eliminating cycles.

4.1. Overview

We describe the Chiu-Liu algorithm with the following flowchart:

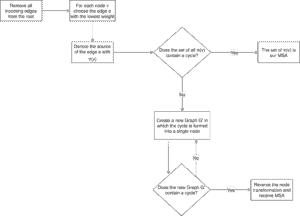
First of all, we eliminate all the edges that lead into the root, since the root of an MSA has no incoming edges. Secondly, we have a look at each node in the graph and select its lowest incoming edge e, denoting its source with $\pi(v)$ . Then we check if we already have an MSA or not. If not we recursively eliminate the cycles in the graph.

4.2. Eliminating Cycles

To get a better perspective we have another look at the step in which we transform a cycle into a single node:

For all nodes that are in $V$ and not in $C$ , we create a set $V'$ with a new weight function $w'$ .
For all edges that connect to a node in $V$ we exercise the following rule, creating a new set of edges $E'$ :

1. For an edge $(u,v)$ with $u \notin C$ and $v \in C$ we create a new edge $e = (u,v_c)$ in $E'$ and define $w'(e) = w(u,v) - w(\pi(v),v)$ .
2. For an edge $(u,v)$ with $u \in C$ and $v \notin C$ we create a new edge $e = (v_c, v)$ in $E'$ and define $w'(e) = w(u,v)$ .
3. For all edges with nodes not included in the circle we keep the edges and edgweights from the original graph.

We do this reduction until we have a Graph $G'$ that does not contain any cycles. Since the constructed $G'$ doesn’t have any cycles we have an MSA. Now we only have to transform $G'$ back into a graph with all of the original nodes.

For this, we have a look at our constructed nodes $v_c$ , which have only one incoming edge, namely $u_c$ . This edge corresponds to the edge $(u,v)$ in our original Graph $G$ , with v being in a cycle.

We then proceed to remove the $(\pi(v),v)$ from our original graph, to break the cycle.

Doing this subsequently for every constructed node $v_c$ we end up with a graph that contains all original nodes and is cycle-free. This graph is the solution to our MSA problem.

4.3. Complexity

In our worst-case, we check every node in the graph. And for every node, we have to change the weights of every edge in the graph. Therefore we conclude a time complexity of $O(VE)$ . With a fitting data structure, for example, a Fibonacci heap, the complexity can be reduced to $O(E \cdot V logV)$

5. Conclusion

In this article, we have discussed the reason why we can neither apply the Kruskal nor the Prim algorithm to a directed graph. Furthermore, we have explored an alternative that retrieves a minimum spanning arborescence for a given directed graph and a root node.

Full Archive

About Baeldung

Core Concepts

Operating Systems

Artificial Intelligence

Graph Theory

Latex