Off-policy vs. On-policy Reinforcement Learning

1. Introduction

In this tutorial, we’re going to have a look at two different approaches for training a reinforcement learning agent – on-policy learning and off-policy learning.

We’re going to start by revisiting what they’re supposed to solve, and in the process, we’re going to find out what advantages or disadvantages each one has.

2. Reinforcement Learning Basics

Reinforcement learning, in general, is used when we have a complex environment. The environment can be a game, a track to navigate, or anything really, as long as it can be defined as a series of states $s \in S$ . Our main goal is to find some optimal action policy $\pi^*$ that leads an agent to choose the best action $a$ out of the set of all possible actions $A$ in every given state $s \in S$ . When we find one such policy, we often say that we “solved” the environment.

Here is an example of a learnable environment in which we have a worm trying to navigate toward an apple. The worm, in this case, will be an agent, and the tiles that he can travel on will signify the states. Each state gives out a reward, and in this example, the worm will receive a reward of $-1$ for entering every state except the one containing the apple. If it reaches that state, he gets a reward of positive $5$ :

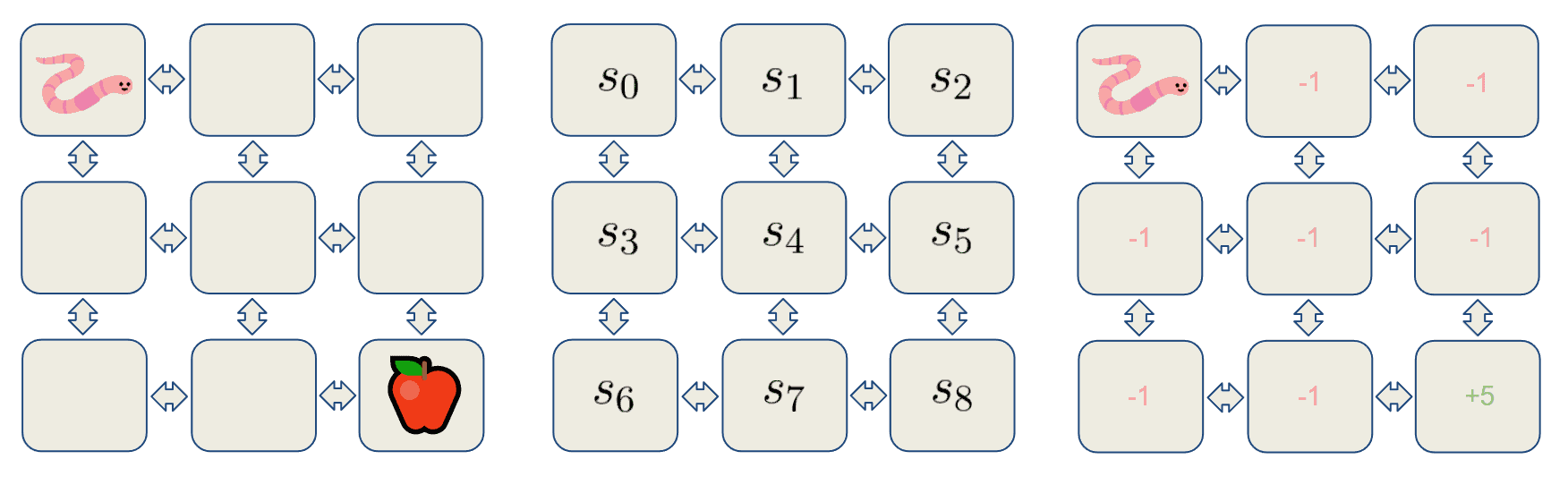
This is a minimal example of an RL problem, but most of the time, the environment involved is quite complex and almost impossible to gain complete knowledge of. This is why we use Monte Carlo methods to sample the environment we’re trying to solve and gain some knowledge about it.

We set out our agent to follow a given policy $\pi$ and interact with the environment until it reaches some terminal state at time $T$ . One such traversal is called an episode and consists of a sequence of states, actions, and rewards that the agent got on his path. To illustrate, let’s set our agent to act upon some policy and collect an episode:

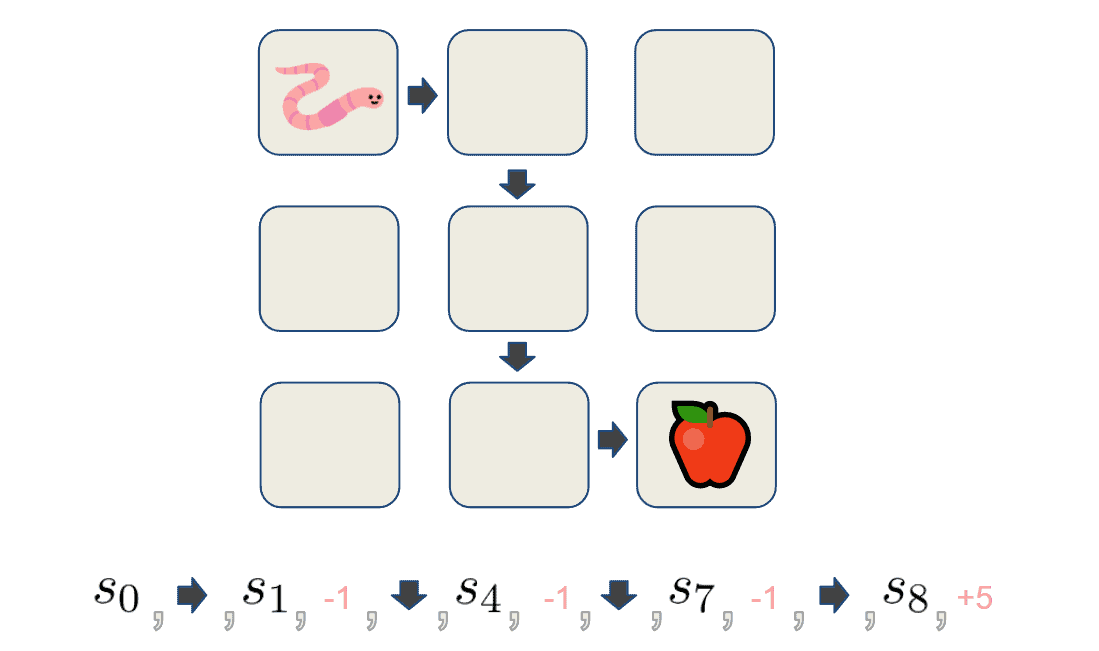
The goal here is to collect many episodes of traversals through the environment like the one above. These can then be used to iteratively estimate the real state-value function $v_\pi(s)$ and/or action-value function $q_\pi(s, a)$ .

The state-value function assigns a value to each state based on the expected cumulative reward $R$ when starting in $s$ and following $\pi$ thereafter. It’s used to assess the quality of a given policy.

The state-action value function, on the other hand, expresses the expected cumulative reward $R$ for a given state $s$ and action $a$ and following $\pi$ thereafter and is used to improve the policy. If we have correct estimates of either of these functions, we can say that we’re done with the task because we can easily construct the optimal policy using their outputs.

3. Exploration vs. Exploitation

The more episodes are collected, the better because the estimates of the functions will be. However, there’s a problem. If the algorithm for policy improvement always updates the policy greedily, meaning it takes only actions leading to immediate reward, actions and states not on the greedy path will not be sampled sufficiently, and potentially better rewards would stay hidden from the learning process.

Essentially, we’re forced to make a choice between making the best decision given the current information or start exploring and finding more information. This is also known as the Exploration vs. Exploitation Dilemma.

We’re looking for something like a middle ground between those. Full-on exploration would mean that we would need a lot of time to collect the needed information, and full-on exploitation would make the agent stuck into a local reward maximum. There are two approaches to ensure all actions are sampled sufficiently called on-policy and off-policy methods.

4. On-policy Methods

On-policy methods solve the exploration vs exploitation dilemma by including randomness in the form of a policy that is soft, meaning that non-greedy actions are selected with some probability. These policies are called $\epsilon$ -greedy policies as they select random actions with an $\epsilon$ probability and follow the optimal action with $1-\epsilon$ probability:

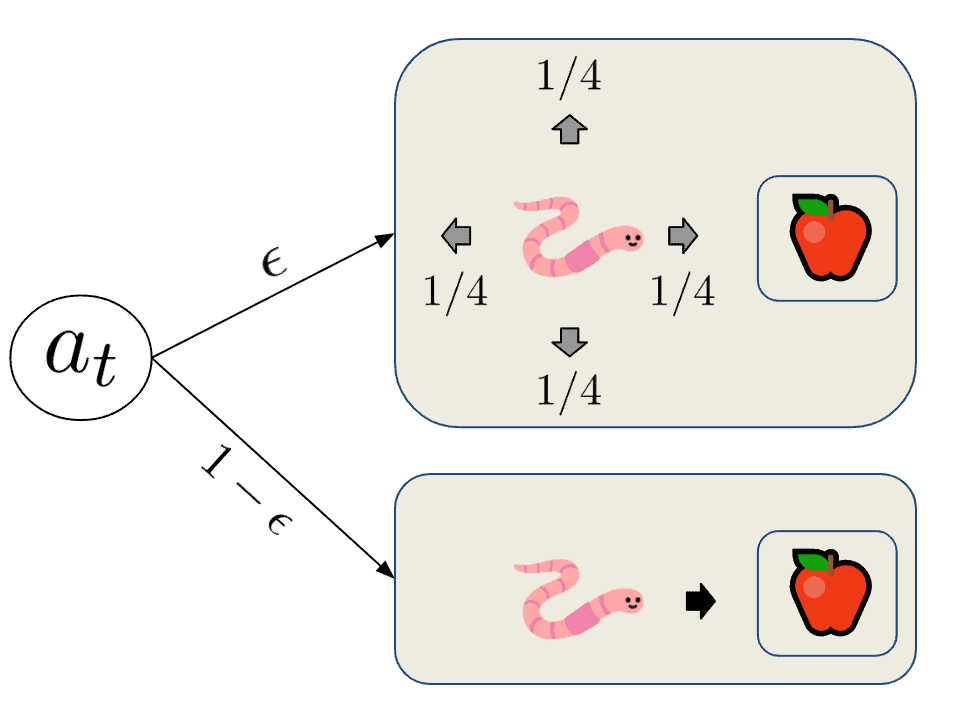
Since the probability of selecting from the action space randomly is $\epsilon$ , the probability of selecting any particular non-optimal action is $\epsilon/|\mathcal{A}(s)|$ . The probability of following the optimal action will always be slightly higher, however, because we have a $1 - \epsilon$ probability of selecting it outright and $\epsilon/|\mathcal{A}(s)|∣$ probability of selecting it from sampling the action space:

$P(a_t^{*}) = 1 - \epsilon+\epsilon/|\mathcal{A}(s)|$

It’s also worth noting that because the optimal action will be sampled more often than the others making on-policy algorithms will generally converge faster but they also have the risk of trapping the agent into a local optimum of the function.

4.1. SARSA

One representative of an on-policy algorithm that uses $\epsilon$ -greedy strategy is state–action–reward–state–action (SARSA). It’s called that way because we’re not using the whole episode to estimate the action-value function $Q$ but the samples ${S_t, A_t, R_{t+1}, S_{t+1}, A_{t+1}}$ from two subsequent time steps:

$Q\left(S_{t}, A_{t}\right) \leftarrow Q\left(S_{t}, A_{t}\right)+\alpha\left(R_{t+1}+\gamma Q\left(S_{t+1}, A_{t+1}\right)-Q\left(S_{t}, A_{t}\right)\right)$

For each state in the episode, SARSA chooses the action $a$ using the $\epsilon$ -greedy policy with respect to the action-value function $Q$ . It receives a reward $R_{t+1}$ and makes a transition to the next state $S_{t+1}$ to make another $\epsilon$ -greedy action $A_{t+1}$ .

5. Off-policy Methods

Off-policy methods offer a different solution to the exploration vs. exploitation problem. While on-Policy algorithms try to improve the same $\epsilon$ -greedy policy that is used for exploration, off-policy approaches have two policies: a behavior policy and a target policy. The behavioral policy $b$ is used for exploration and episode generation, and the target or goal policy $\pi$ is used for function estimation and improvement.

This works because the target policy $\pi$ gets a “balanced” view of the environment and can learn from potential mistakes of $b$ while still keeping track of the good actions and trying to find better ones. However, one thing to remember is that in Off-policy learning, we have a distribution mismatch between the one we’re trying to estimate and the one we’re sampling from. That is why a technique called importance sampling is often used to facilitate this mismatch.

5.1. Q-Learning

A very popular off-policy learning to consider is SARSA Max, also known as $Q$ -learning. Here we’re trying to update the Q function not by choosing $\epsilon$ -greedy actions but rather by always choosing the action with the maximum value:

$Q\left(S_{t}, A_{t}\right) \leftarrow Q\left(S_{t}, A_{t}\right)+\alpha\left(R_{t}-\gamma \max _{a} Q\left(S_{t}, a\right)-Q\left(S_{t}, A_{t}\right)\right)$

We can see that in the formula, we’re updating the function using both $A_t$ , which is chosen by the $\epsilon$ -greedy policy b, and $\max _{a} Q\left(S_{t}, a\right)$ which is selected by the other greedy “max” policy.

6. Conclusion

In this article, we reviewed the basics of reinforcement learning and set out to view two families of approaches – on-policy and off-policy learning. As examples, we took two popular algorithms, SARSA and SARSA Max or Q-learning. We saw how they battled the problem of Exploration vs. Exploitation and what each approach has to offer.

Full Archive

About Baeldung

Core Concepts

Operating Systems

Artificial Intelligence

Graph Theory

Latex