Intersection Over Union for Object Detection | Baeldung on Computer Science

1. Overview

In this article, we’ll talk about the Intersection over Union (IoU), a popular metric for evaluating object detection techniques.

First, we’ll explain the geometrical meaning of IoU. Then, we’ll illustrate how to calculate this metric. Finally, we’ll provide the pseudocode and a simple example of the IoU computation.

2. What Is Intersection Over Union?

In object detection, our task is to locate and classify objects in an image. To do so, we capture them with bounding boxes, each with a class label representing the object we detected in the box.

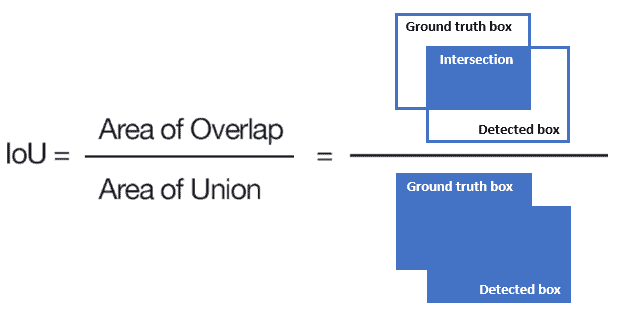
The IoU measures the accuracy of our detections. Given a ground-truth bounding box and a detected bounding box, we compute the IoU as the ratio of the overlap and union areas:

Here are some examples of different IoU values:

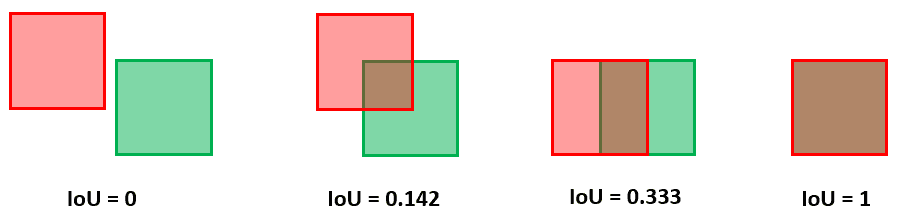
The IoU can have any value between 0 and 1. If two boxes do not intersect, the IoU is 0. On the other hand, if they completely overlap, the intersection and the union areas are equal. So, in that case, the IoU is 1.

Therefore, the higher the IoU, the better the prediction of an object detection system.

3. How to Compute IoU?

We assume a coordinate system with the positive x-axis moving to the right and the positive y-axis moving downward. A bounding box is defined by the left (L), right (R), top (T), and bottom (B).

Let’s start by calculating the coordinates of the intersection rectangle. Given a pair of bounding boxes, there are two different ways to name the coordinates (cases 1 and 2):

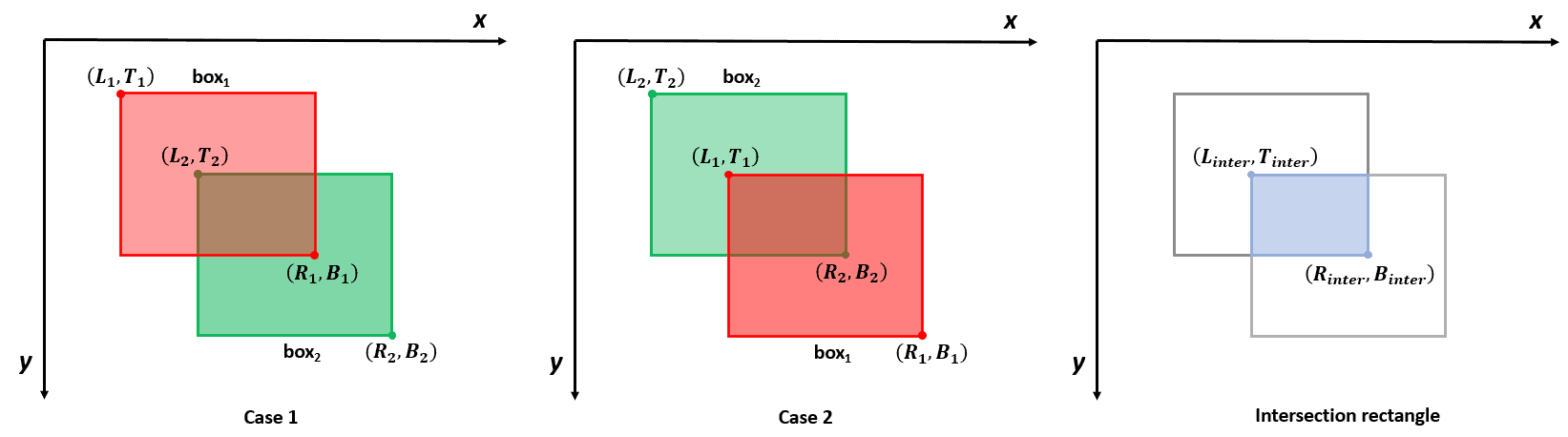
In both cases, the left side of the intersection $L_{inter}$ is the rightmost left margin of the two bounding boxes. Similarly, the top of the intersection $T_{inter}$ is the lower top margin of the two boxes. Therefore, the intersection’s left-top coordinates are:

(1) $\begin{equation*} L_{inter} = \max ( L_1, L_2) \end{equation*}$

(2) $\begin{equation*} T_{inter} = \max (T_1, T_2) \end{equation*}$

The right side of the intersection $R_{inter}$ is the leftmost right margin of the two boxes. Similarly, the bottom of the intersection $B_{inter}$ is the higher bottom margin of the two boxes. Hence, the interesection’s bottom-right coordinates are:

(3) $\begin{equation*} R_{inter} = \min( R_1, R_2) \end{equation*}$

(4) $\begin{equation*} B_{inter} = \min(B_1, B_2) \end{equation*}$

The intersection area $A_{inter}$ can be easily computed from the obtained coordinates:

(5) $\begin{equation*} A_{inter} = (R_{inter} - L_{inter} ) \times (B_{inter} - T_{inter}) \end{equation*}$

Let’s now compute the area of the union. First we calculate the area of the two boxes:

(6) $\begin{equation*} A_1 = (R_1 - L_1)\times (B_1 - T_1) \end{equation*}$

(7) $\begin{equation*} A_2= (R_2 - L_2) \times (B_2 - T_2) \end{equation*}$

The union area $A_{union}$ is computed as:

(8) $\begin{equation*} A_{union} = A_1 + A_2 - A_{inter}\end{equation*}$

it is worth noting that intersection area is include in both $A_1$ and $A_2$ , hence $A_{inter}$ is subtracted to $(A_1 + A_2 )$ in order to count the intersection area only once.

Finally, we can calculate the IoU:

(9) $\begin{equation*} \text{IoU} = {A_{inter} \over A_{union} }\end{equation*}$

4. Pseudocode

Here’s the pseudocode of the IoU computation:

The algorithm requires 8 input values, i.e., the coordinates of the two bounding boxes. The intersection and the union areas are computed as described previously. When $(R_{inter} < L_{inter})$ or $(B_{inter} < T_{inter})$ , the boxes do not intersect, hence the algorithm returns 0.

5. Example

Let’s consider the two boxes with coordinates:

$\text{box}_1= [L_1, T_1, R_1, B_1] = [0, 0, 10, 10]$

$\text{box}_2= [L_2, T_2, R_2, B_2] = [5, 5, 15, 15]$

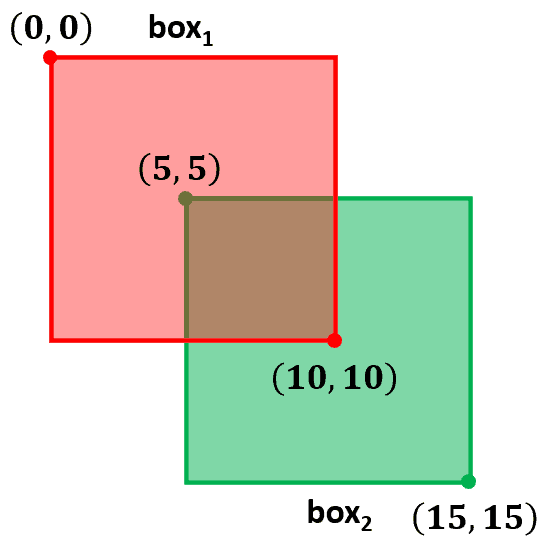
The coordinates of the intersection rectangle are:

$[L_{inter}, T_{inter}, R_{inter}, B_{inter}] = [5, 5, 10, 10]$

So, the intersection area is:

$A_{inter} = (10 - 5) \times (10 - 5) = 5 \times 5 = 25$

Each box has an area of $100$ , so the union area is:

$A_{union} = 100 + 100 - 25 = 175$

Finally, the IoU is:

$\text{IoU} = {25 \over 175} = 0.142$

6. Computational Complexity

The algorithm always requires 8 input values. Hence, the spatial complexity and time complexity are both constant, i.e., $\mathcall{O}(1)$ .

7. Conclusion

In this article, we explained the IoU metric for object detection in images. We defined it geometrically and explained how to calculate it. Finally, we provided the pseudocode and an example of the IoU computation.

Full Archive

About Baeldung

Core Concepts

Operating Systems

Artificial Intelligence

Graph Theory

Latex