Learn through the super-clean Baeldung Pro experience:
>> Membership and Baeldung Pro.
No ads, dark-mode and 6 months free of IntelliJ Idea Ultimate to start with.
Last updated: February 28, 2025
Computing the similarity between two text documents is a common task in NLP, with several practical applications. It has commonly been used to, for example, rank results in a search engine or recommend similar content to readers.
Since text similarity is a loosely-defined term, we’ll first have to define it for the scope of this article. After that, we’ll explore two different ways of computing similarity and their pros and cons.
Our first step is to define what we mean by similarity. We’ll do this by starting with two examples.
Let’s consider the sentences:
Although they convey a very similar meaning, they are written in a completely different way. In fact, the two sentences just have one word in common (“the”), and not a really significant one at that.
Nevertheless, it’s safe to say that we’d want an ideal similarity algorithm to return a high score for this pair.
Now let’s change the sentences a little bit:
We only changed two words, yet the two sentences now have an opposite meaning.
When we want to compute similarity based on meaning, we call it semantic text similarity. Due to the complexities of natural language, this is a very complex task to accomplish, and it’s still an active research area. In any case, most modern methods to compute similarity try to take the semantics into account to some extent.
However, this may not always be needed. Traditional text similarity methods only work on a lexical level, that is, using only the words in the sentence. These were mostly developed before the rise of deep learning but can still be used today. They are faster to implement and run and can provide a better trade-off depending on the use case.
In the rest of the article, we’ll not cover advanced methods that are able to compute fine-grained semantic similarity (for example, handling negations). Instead, we’ll first cover the foundational aspects of traditional document similarity algorithms. In the second part, we’ll then introduce word embeddings which we can use to integrate at least some semantic considerations.
The traditional approach to compute text similarity between documents is to do so by transforming the input documents into real-valued vectors. The goal is to have a vector space where similar documents are “close”, according to a chosen similarity measure.
This approach takes the name of Vector Space Model, and it’s very convenient because it allows us to use simple linear algebra to compute similarities. We just have to define two things:
So, let’s see the possible ways of transforming a text document into a vector.
The simplest way to build a vector from text is to use word counts. We’ll do this with three example sentences and then compute their similarity. After that, we’ll go over actual methods that can be used to compute the document vectors.
Let’s consider three sentences:
To build our vectors, we’ll count the occurrences of each word in a sentence:
| Document 1 | Document 2 | Document 3 | |||
|---|---|---|---|---|---|
| we | 1 | I | 1 | there’s | 1 |
| went | 1 | ate | 1 | no | 1 |
| to | 1 | pizza | 1 | place | 1 |
| the | 1 | with | 1 | like | 1 |
| pizza | 2 | you | 1 | home | 1 |
| place | 1 | yesterday | 1 | ||
| and | 1 | at | 1 | ||
| you | 1 | home | 1 | ||
| ate | 1 | ||||
| no | 1 | ||||
| pizza | 1 | ||||
| at | 1 | ||||
| all | 1 |
Although we didn’t do it in this example, words are usually stemmed or lemmatized in order to reduce sparsity.
Once we have our vectors, we can use the de facto standard similarity measure for this situation: cosine similarity. Cosine similarity measures the angle between the two vectors and returns a real value between -1 and 1.
If the vectors only have positive values, like in our case, the output will actually lie between 0 and 1. It will return 0 when the two vectors are orthogonal, that is, the documents don’t have any similarity, and 1 when the two vectors are parallel, that is, the documents are completely identical:
If we apply it to our example vectors we’ll get:
As we can see, the first two documents have the highest similarity, since they share three words. Note that since the word pizza appears two times it will contribute more to the similarity compared to “at”, “ate” or “you”.
The simplified example we’ve just seen uses simple word counts to build document vectors. In practice, this approach has several problems.
First of all, the most common words are usually the less significant ones. In fact, most documents will share many occurrences of words like “the”, “is”, and “of” which will impact our similarity measurement negatively.
These words are commonly referred to as stopwords and can be removed in a preprocessing step. Nonetheless, a more sophisticated approach like TF-IDF can be used to automatically give less weight to frequent words in a corpus.
The idea behind TF-IDF is that we first compute the number of documents in which a word appears in. If a word appears in many documents, it will be less relevant in the computation of the similarity, and vice versa. We call this value the inverse document frequency or IDF, and we can compute it as:
In the formula, is the corpus,
is the total number of documents in it, and the denominator is the number of documents that contain our word. For example, if we use the previous three sentences as our corpus, the word “pizza” will have an IDF equal to:
while the word “yesterday”:
assuming we use base-10 logarithm. Note that if a word were to appear in all three documents, its IDF would be 0.
We can compute the IDF just once, as a preprocessing step, for each word in our corpus and it will tell us how significant that word is in the corpus itself.
At this point, instead of using the raw word counts, we can compute the document vectors by weighing it with the IDF. For each document, we’ll compute the count for each word, transform it into a frequency (that is, dividing the count by the total number of words in the document), and then multiply by the IDF.
Given that, the final score for each word will be:
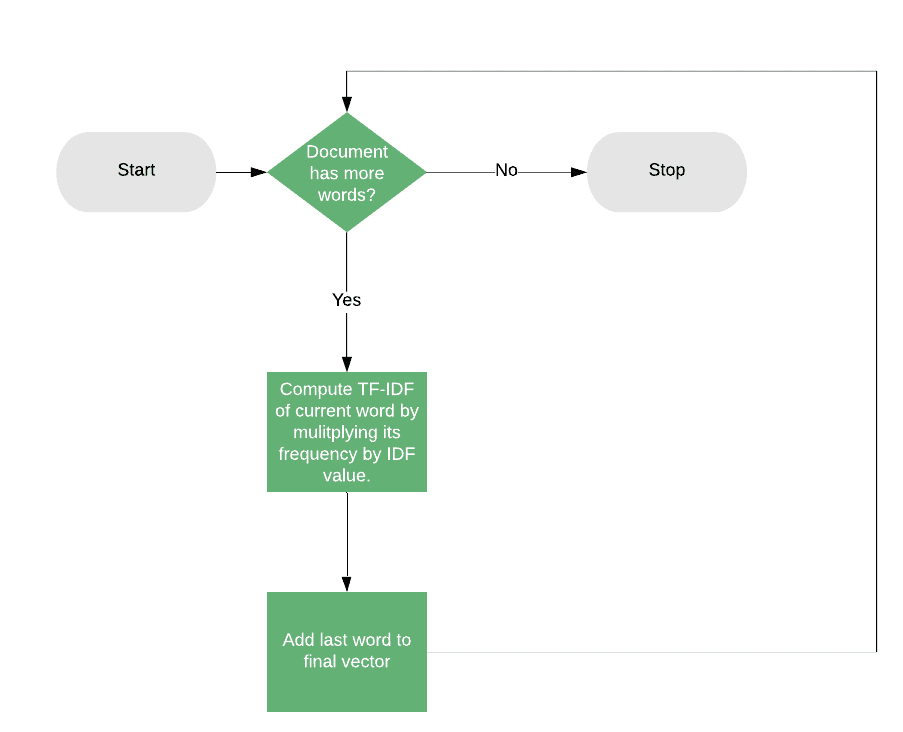
The weighting factor provided by this method is a great advantage compared to using raw word frequencies, and it’s important to note that its usefulness is not limited to the handling of stopwords.
Every word will have a different weight, and since word usage varies with the topic of discussion, this weight will be tailored according to what the input corpus is about.
For example, the word “lawyer” could have low importance in a collection of legal documents (in terms of establishing similarities between two of them), while, instead, high importance in a set of news articles. Intuitively this makes sense because most legal documents will talk about lawyers, but most news articles won’t.
The downside of this method as described is that it doesn’t take into account any semantic aspect. Two words like “teacher” and “professor”, although similar in meaning, will correspond to two different dimensions of the resulting document vectors, contributing 0 to the overall similarity.
In any case, this method or variations of it, are still very efficient and widely used, for example in implementing search engine results ranking. In this scenario, we can use the similarity between the input query and the result documents to rank higher those that are very similar.
Word embeddings are high-dimensional vectors that represent words. We can create them in an unsupervised way from a collection of documents, in general using neural networks, by analyzing all the contexts in which the word occurs.
This results in vectors that are similar (according to cosine similarity) for words that appear in similar contexts, and thus have a similar meaning. For example, since the words “teacher” and “professor” can sometimes be used interchangeably, their embeddings will be close together.
For this reason, using word embeddings can enable us to handle synonyms or words with similar meaning in the computation of similarity, which we couldn’t do by using word frequencies.
However, word embeddings are just vector representations of words, and there are several ways that we can use to integrate them into our text similarity computation. In the next section, we’ll see a basic example of how we can do this.
The simplest way to compute the similarity between two documents using word embeddings is to compute the document centroid vector. This is the vector that’s the average of all the word vectors in the document.
Since word embeddings have a fixed size, we’ll end up with a final centroid vector of the same size for each document which we can then use with cosine similarity.
This method is not optimal since, especially for long documents, averaging all the words leads to a loss of information. However, in some cases, for example for small documents, it could be a good solution that solves the problems of our previous approach in handling different but similar words.
Note that we could also integrate a weighting factor in the computation of the centroid vector, and this could be the same TF-IDF weighting strategy described above. To do this, when computing the centroid, we can multiply each word embedding vector by its TF-IDF value, then do a weighted average:
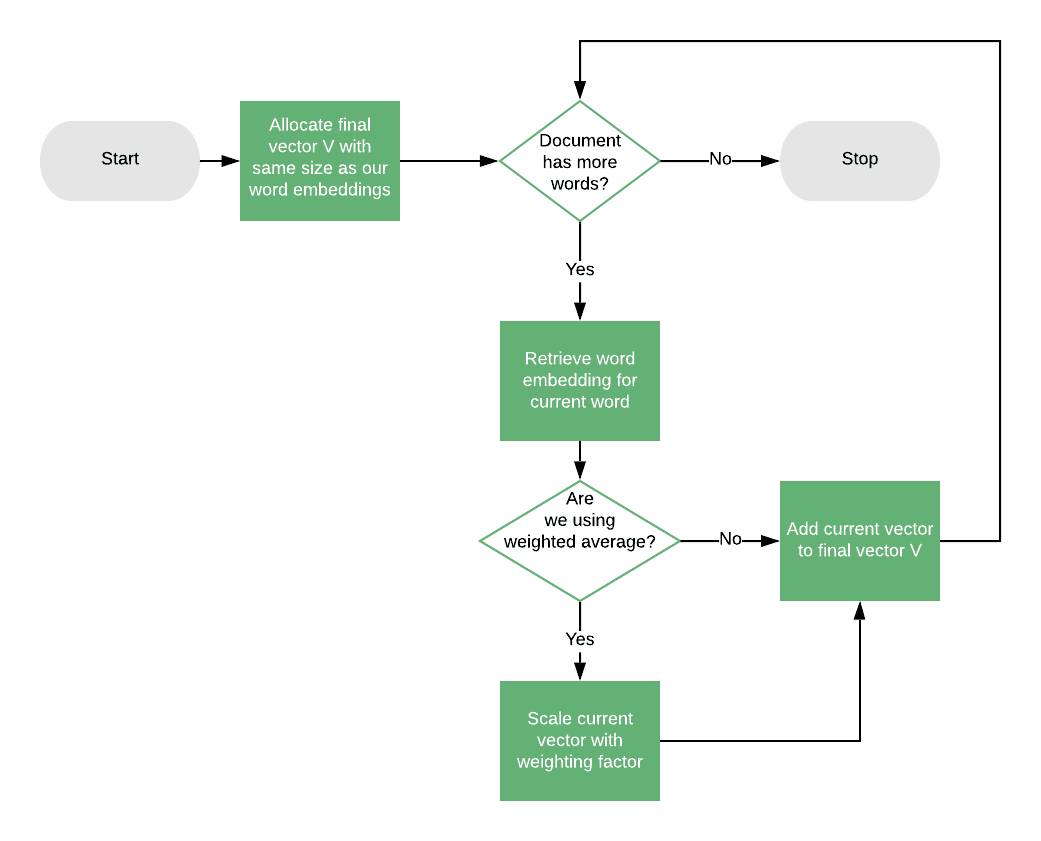
Word embeddings have the advantage of providing rich representations for words, way more powerful than using the words themselves. However, in terms of a text similarity algorithm, they don’t provide a direct solution, but they are rather a tool that can help us improve an existing one.
They are useful because they allow us to go beyond a basic lexical level, but we need to evaluate if this is necessary because they add extra complexity.
Text similarity is a very active research field, and techniques are continuously evolving and improving. In this article, we’ve given an overview of possible ways to implement text similarity, focusing on the Vector Space Model and Word Embeddings.
We’ve seen how methods like TF-IDF can help in weighting terms appropriately, but without taking into account any semantic aspects. On the other hand, Word Embeddings can help integrating semantics but have their own downsides.
For these reasons, when choosing what method to use, it’s important to always consider our use case and requirements carefully.