How to Find the Two Points With the Minimal Manhattan Distance

1. Introduction

In this tutorial, we’ll show how to find the pair of 2D points with the minimal Manhattan distance.

2. The Minimal Manhattan Distance

Let’s say that we have $n$ two-dimensional points $Z = \{z_i\}_{i=1}^{n}, z_i = (x_i, y_i), i = 1, 2, \ldots, n$ . We want to find the two closest per the Manhattan distance. It measures the length of the shortest rectilinear path between two points that contains only vertical and horizontal segments:

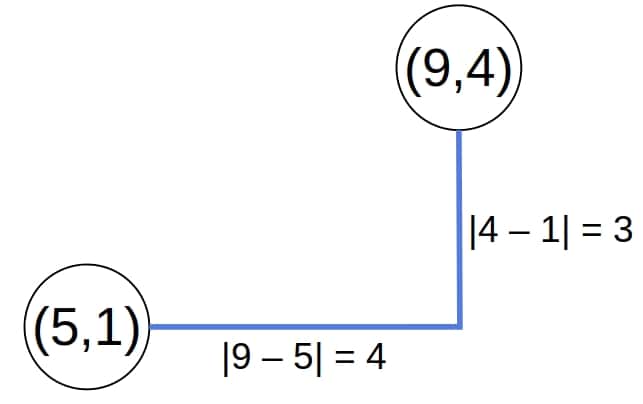
So, the formula for computing the Manhattan distance is:

(1) $\begin{equation*} d_{M} \left( (x_i, y_i), (x_j, y_j)\right) = |y_j - y_i| + |x_j - x_i| \end{equation*}$

3. Algorithm

We can follow the brute-force approach and iterate over all $\binom{n}{2}$ pairs of points, calculating the distance between each two and returning the closest pair. However, that algorithm’s time complexity is quadratic.

Instead, we could design a more efficient algorithm using the divide-and-conquer strategy. Finding the closest pair is a fundamental problem of computational geometry, so it’s necessary to have a fast method for solving it.

3.1. The Divide-and-Conquer Approach

Let’s draw a line through $Z$ to split it into the left and right halves, $P$ and $Q$ :

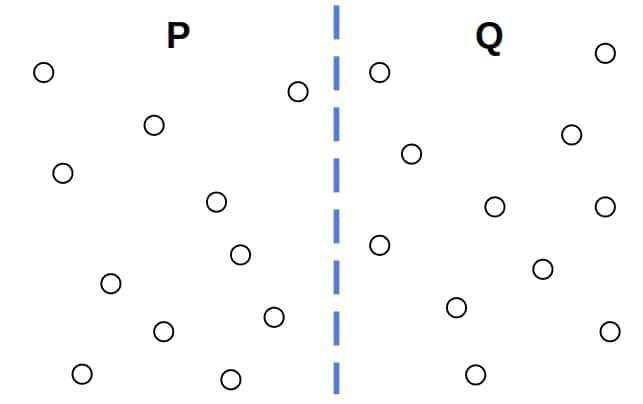
Now, the closest pair in the whole $Z$ is either the closest pair in $P$ , the closest pair in $Q$ , or the closest pair whose one point is in $P$ and the other in $Q$ :

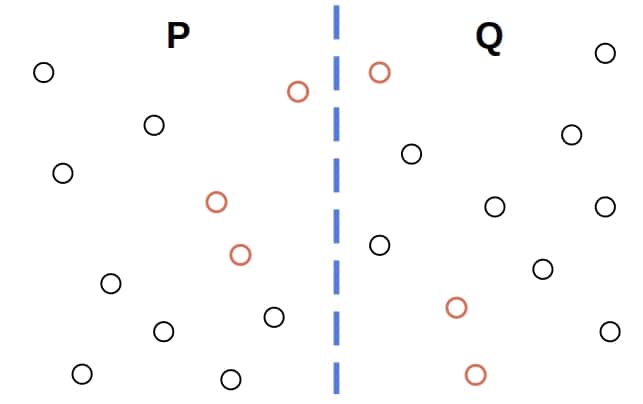
Therefore, to find the closest pair in $\boldsymbol{Z}$ , we first need to determine the closest pair in its left and right halves. That’s the step where we break the original problem into two smaller sub-problems. Let’s say that $\delta_P$ is the minimal distance in $P$ and $\delta_Q$ is the minimal distance in $Q$ . With $\delta = \min \{ \delta_P, \delta_Q\}$ , the closest two points in $\boldsymbol{P \times Q}$ are at a distance shorter than $\boldsymbol{\delta}$ only if they reside in the $\boldsymbol{2\delta}$ -wide strip along the dividing line:

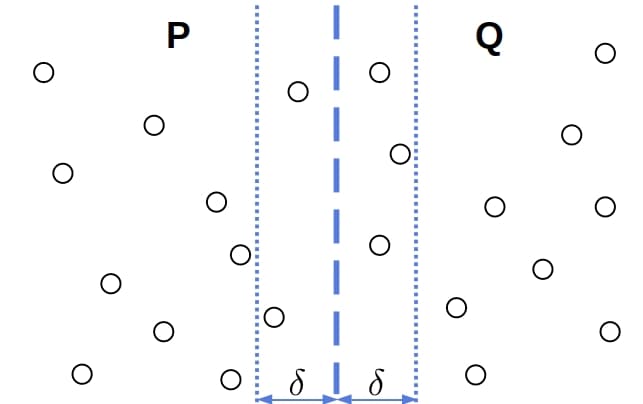
So, the combination step consists of finding the strip’s minimal distance $\delta'$ and comparing it to $\delta$ .

That gives a recursive algorithm. As the base case, we’ll take $Z$ that contains three points and solve it by inspecting all three pairs, but there are other choices.

3.2. The Worst-Case Running Time Analysis

Let $T(n)$ be the worst-case running time for the input with $n$ points, and let $f(n)$ denote the cost of finding $\delta'$ and dividing $Z$ into $P$ and $Q$ . Then, we have the following recurrence:

(2) $\begin{equation*} T(n) = 2 T \left( \frac{n}{2} \right) + f(n) \end{equation*}$

Scanning through $P$ and $Q$ to remove all the points not in the $2 \delta$ -wide strip takes $O(n)$ time, so $f(n) \in \Omega(n)$ . In the worst case, all the pairs $(p, q) \in P \times Q$ can be in the strip, so an enumerative approach performs $\frac{n^2}{4} \in O(n^2)$ steps and the recurrence becomes:

$T(n) = 2 T \left( \frac{n}{2} \right) + O(n^2)$

Using the Master Theorem, we get $T(n) \in O(n^2)$ . But, that isn’t any better than the inefficient brute-force algorithm, and we didn’t even consider the cost of splitting $Z$ . Can we do anything to make the algorithm faster? Luckily, the points in the strip have a special structure that will enable us to find $\delta'$ quickly. Indeed, if we implemented the algorithm so that $\boldsymbol{f(n) \in O(n)}$ , the recurrence (2) would evaluate to an $\boldsymbol{O(n \log n)}$ solution.

3.3. The Vertical Manhattan Strip Has a Special Structure

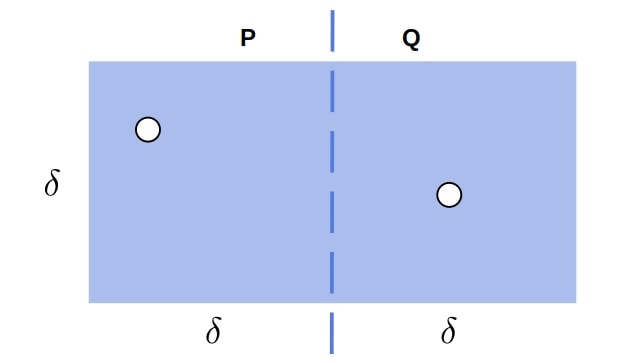
Let’s assume that the closest two points $(p, q)$ in $Z$ are in the strip ( $p \in P, q \in Q$ ). Because $\delta' < \delta$ , we can be sure that vertically, they can’t be more than $\delta$ apart:

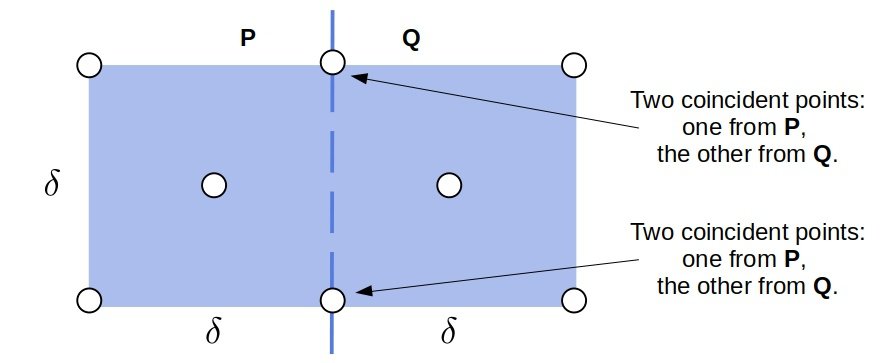
How many other points from $P$ and $Q$ can be in the $2\delta \times \delta$ rectangle containing $p$ and $q$ ? Since all the points $\boldsymbol{\in P}$ are at distances $\boldsymbol{\geq \delta}$ , at most five points from $\boldsymbol{P}$ can reside in the left half of the rectangle, and the same goes for $\boldsymbol{Q}$ :

So, if we sorted the points in the strip by the $y$ -coordinates, the indices of $p$ and $q$ would differ at most by 9. Therefore, for each point in the strip, we need to check only the nine that follow it in the $y$ -sorted array. As a result, we can find $\delta'$ in a linear time. But, if we sort the points in each recursive call, we’ll have $f(n) \in O(n \log n)$ , and we need $f(n)$ to be linear in $n$ for the whole algorithm to be log-linear.

3.4. Sorting

We achieve that by presorting. If we sorted $\boldsymbol{Z}$ by the $\boldsymbol{y}$ -axis beforehand, we could split the points into the $\boldsymbol{y}$ -sorted $\boldsymbol{P}$ and $\boldsymbol{Q}$ in each call in a linear time. Let’s denote the $y$ -sorted copy of $Z$ as $Y$ .

Since we partition $Z$ by the points’ $x$ -coordinates, we should also keep a copy of $Z$ sorted by $x$ (let’s denote it as $X$ ). Then, we can use the middle copy’s middle index to split $Z$ into the left and right halves in $O(1)$ time. Before making the recursive calls, we need to split $X$ and $Y$ into their $P$ and $Q$ parts just as we split $Z$ into $P$ and $Q$ . We do that in linear time by reversing the merge step of Merge sort:

Presorting can be done in the $O(n \log n)$ worst-case time by Merge sort. With $f(n) \in O(n)$ , our algorithm also takes $O(n \log n)$ time, so the total complexity doesn’t suffer by presorting.

3.5. The Pseudocode

Finally, here’s the pseudocode of the whole algorithm:

3.6. What If We Didn’t Use the Manhattan Distance?

The only part where we use the properties of the Manhattan distance is the analysis of the maximal number of points we can fit into a $2 \delta \times \delta$ rectangle centered at the vertical line so that the distance of each two from the same half is at most $\delta$ .

If we use other distance functions, the rectangle’s structure will change. For example, the Euclidean distance $\sqrt{(x_i-x_j)^2 + (y_i-y_j)^2}$ admits at most 8 points:

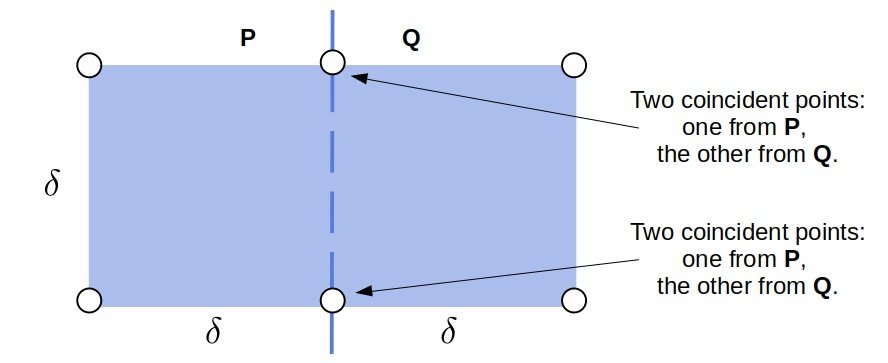
So, we wouldn’t need to check more than seven points following each one in the filtered $Y$ .

4. Conclusion

In this article, we showed how to find the closest two points in a two-dimensional space endowed with the Manhattan distance.

Full Archive

About Baeldung

Core Concepts

Operating Systems

Artificial Intelligence

Graph Theory

Latex