1. Introduction
We know that we can represent pixel colors as numbers, but what use are those numbers?
In this tutorial, we define and talk about image histograms.
2. Definition
We can define the histogram of an image as a 2D bar plot. The horizontal axis represents the pixel intensities. The vertical axis denotes the frequency of each intensity.
Before diving into our first example, let’s state that we’ll consider an image to be a matrix or matrices of pixels. In the case of a grayscale image, this matrix will be made of numbers between 0 and 255. For RGB images, we’ll have three matrices, one of each color channel. For instance:
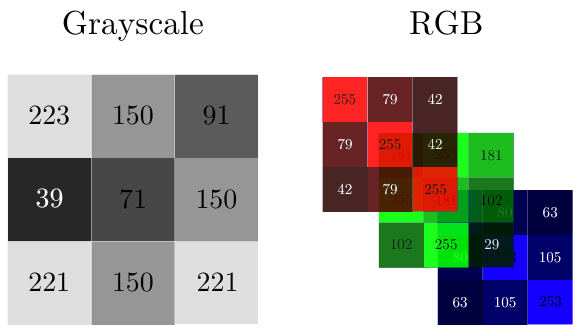
In this way, a black-and-white image with a resolution of 3×3 pixels can be represented as 9 elements ranging from 0-255 in a 3×3 matrix. The same goes for each color channel (RGB) of color images.
2.1. Histograms
To determine the histogram of an image, we need to count how many instances of each intensity we have.
So, a histogram will allow us to see how often each intensity occurs. In our example, the intensity 150 can be seen in three pixels, for this reason, it will have a higher frequency in the histogram (the corresponding bar’s height is 3):
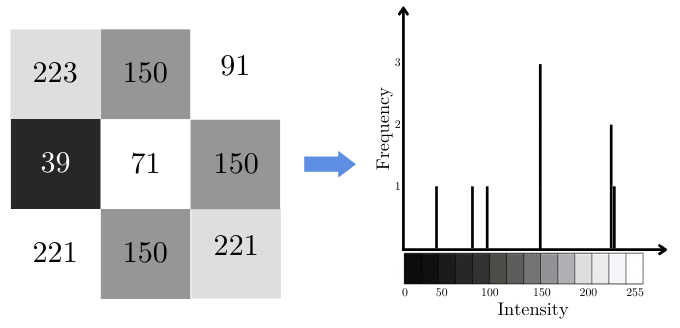
3. Applications
There are many different fields in which histograms are convenient. For example, computer vision, image processing, and photography, to name just three. In this section, we’ll talk about some common applications of histograms.
3.1. Histogram for Image Segmentation
We can use histograms to define the threshold for image segmentation to isolate the background from an object.
For instance, if we want to isolate a rose in the following image from its background, we can start by analyzing its histogram. In this way, we can see that most of the background pixels are white or whiteish. This means that most of the background pixels are close to 255:
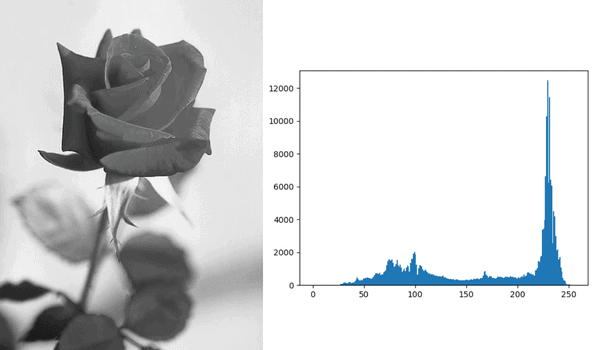
If we define our threshold as 156, and take every pixel > 156 to belong to the background, we’ll get a binary image in which the rose is clearly separated:
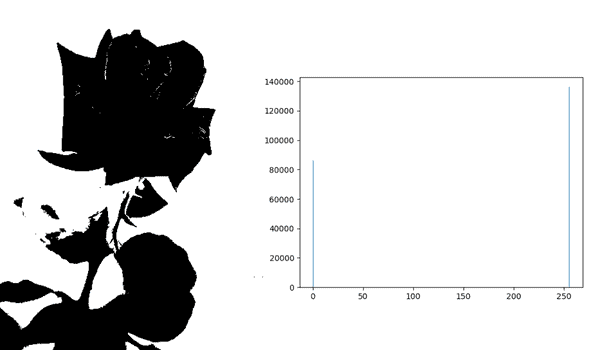
Since the segmented image is binary (a pixel is either a part of the rose or the background), the new histogram has only two possible values. Using different thresholds results in different segmentations.
3.2. Histograms in Photography
In photography, we use histograms to enhance pictures by changing some of their properties. This might help us get clearer pictures or even more beautiful photos.
We’ll illustrate the use of histogram equalization to improve an image’s contrast. We’ll essentially stretch out the histogram. So, if we have underpopulated regions for certain intensities, these regions will have more pixels after processing, which is in this case called equalization.
We won’t go over histogram equalization techniques. Instead, we’ll focus on the result of this operation.
In our example, there are almost no pixels after the intensity 175. After equalization, our image becomes clearer and the pixels are more equally distributed. For example:
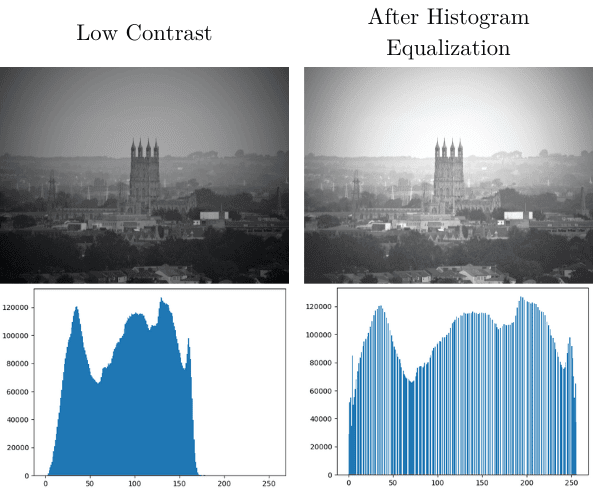
As we see, the resulting image has better contrast, which is what we wanted to achieve.
3.3. RGB Histograms
We can also perform histogram equalization in color images. In that case, the simplest approach is to equalize each RGB channel separately:
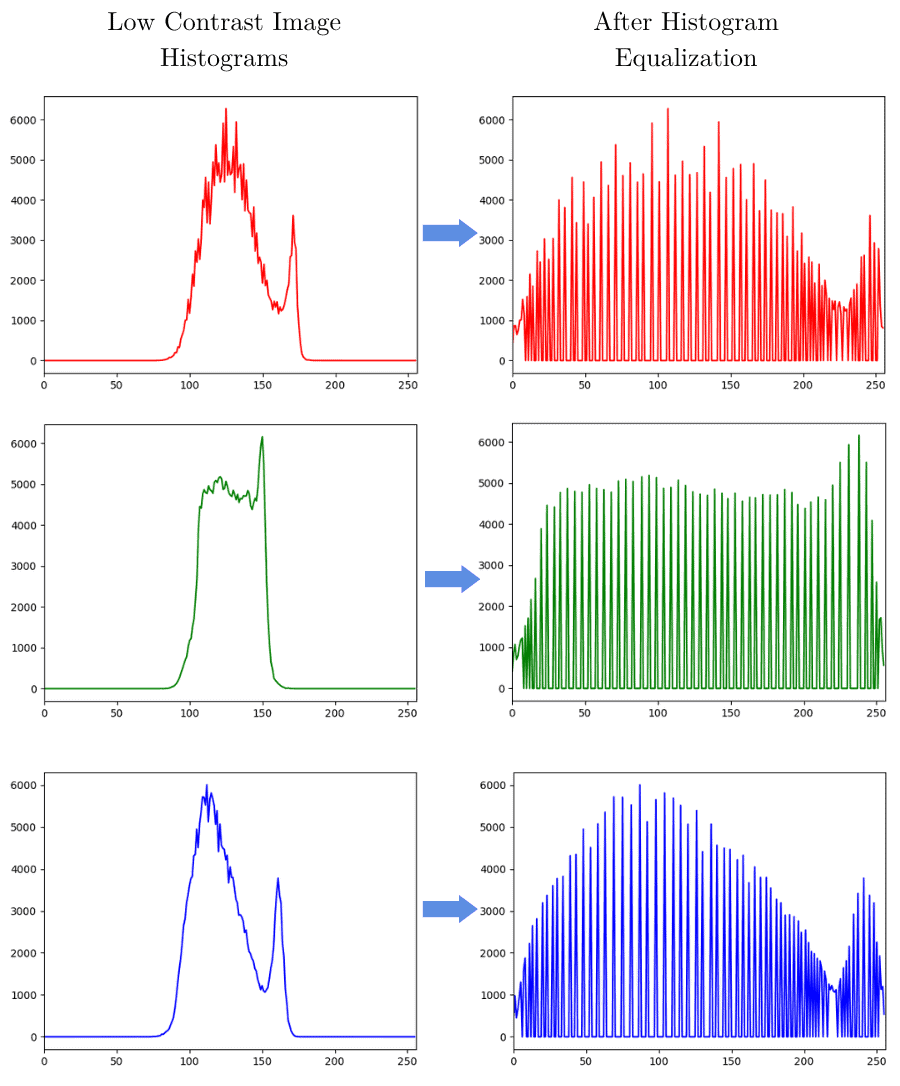
After that, we merge the channels and histograms. For instance:
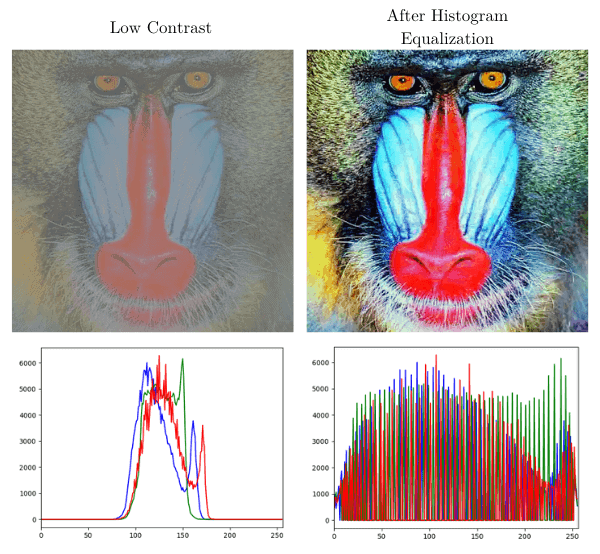
Again, equalization results in a higher-quality image.
4. Conclusion
In this article, we discussed what an image histogram represents both for grayscale and color images. Although a histogram is a relatively simple concept, it has a wide range of use cases.
Moreover, we illustrated some applications to prove histograms’ importance in the photography and image-processing fields.