Time Complexity of Inserting into a Heap

1. Overview

Heap is a popular tree-based data structure. A common operation in a heap is to insert a new node.

In this tutorial, we’ll discuss how to insert a new node into the heap. We’ll also present the time complexity analysis of the insertion process.

2. Insertion Algorithm

Let’s first see the insertion algorithm in a heap then we’ll discuss the steps in detail:

algorithm Insertion(B, N, newValue):
    // INPUT
    //     B = input array
    //     N = starting index
    //     newValue = new node to insert
    // OUTPUT
    //     Heap tree with the new node

    N <- N + 1
    B[N] <- newValue
    k <- N

    while k > 1:
        PNode <- k / 2
        if B[PNode] < B[k]:
            swap(B[PNode], B[k])
            k <- PNode
        else:
            return

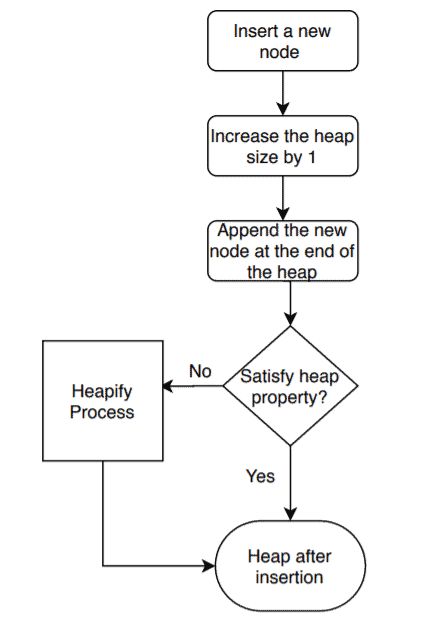
Our input consists of an array , the size of the heap , and the new node that we want to insert. We use to denote the parent node. First, we create a space in a heap to add the new node. The new element is appended at the end of the heap initially.

There is a possibility that the newly inserted node may distort the heap property. To check, we run the heapify process. Heapify operation checks each subtree from the bottom-up fashion and makes sure it follows the heap property.

In the heapify process, we compare a node’s value with its parent’s value. If they aren’t in the correct order, swap them based on the type of heap (max or min-heap).

We present the insertion process in a summarized form here:

3. Time Complexity Analysis

Let’s consider a scenario when we insert a new node in a max-heap, and the key value of the parent of the newly inserted node is greater than the key value of the newly inserted node. In such a case, we don’t need to do anything, and there is no change needed in the max-head as it obeys the heap property.

This is an example of a best-case when inserting a new element in a heap. In such cases, the time required for insertion would be .

In the worst case, the newly inserted node has to be swapped at each level from the bottom up to the root node to maintain the heap property. Now we know that a heap tree is a balanced complete tree data structure.

In the worst case, we need one swap at each level of the tree. So the total number of the swaps would be equal to the height of the heap tree. The height of a balanced complete tree with number of nodes is . Each swap takes time.

Therefore, in the worst case, the time complexity of inserting a node in a heap would be .

4. Conclusion

In this tutorial, we’ve discussed the heap insertion algorithm. We also presented a time complexity analysis for the insertion algorithm.