1. Introduction
In graph theory, the K-Core of a graph is a maximal subgraph in which every vertex has at least degree . K-Cores are used to identify the most tightly connected parts of a graph and can provide insights into the overall structure and behavior of a network.
In this tutorial, we’ll learn about the concept of K-Cores, how to compute them, and their various applications.
2. Overview
The concept of a K-Core in graph theory is a valuable tool for analyzing the structure and connectivity of complex networks. A K-Core is a subgraph of a graph where every vertex in the subgraph has a degree of at least . Essentially, it represents the core of the network, where the most connected and tightly integrated vertices are located.
3. Properties of K-Core
K-core is a subgraph of a larger graph that is maximally connected, meaning that each vertex in the K-Core is connected to at least other vertices in the K-Core. We define the size of the K-Core as the largest value of
for which a K-Core exists in the graph.
The K-Core has several important properties in network science:
- Size: The size of the K-Core is related to the overall connectivity of the graph. The larger the K-Core, the more connected the graph is. We can use this property to understand how well a network can function and how robust it is in removing nodes or edges
- Connectivity: The connectivity of the K-Core is related to the number of edges that need to be removed to break the K-Core into smaller connected components. We can use this property to identify a network’s most central and important nodes
- Identification of subgraphs: The K-Core can identify the most tightly connected subgraphs in a larger graph. These subgraphs will help us understand the network’s overall structure and identify clusters of related nodes
Overall, the K-Core is a valuable tool in network science, as it allows us to better understand the structure and behavior of complex networks.
4. Finding the K-Core of a Graph
We can use several algorithms to find a graph’s K-Core, including degree pruning, color-coding, and K-shell decomposition.
In degree pruning, we start listing vertices with degrees less than k. We then iteratively remove a vertex with a degree less than from the graph and all its incident edges until no such vertices remain. The resulting subgraph is then the K-Core of the original graph.
In color-coding, we assign a color to each vertex based on its degree. Vertices with degrees less than are assigned a color indicating their degree, while those with degrees greater than or equal to
are assigned the same color. We then iteratively remove vertices with the lowest degree colors until no such vertices remain. The resulting subgraph is again the K-Core of the original graph.
K-shell decomposition is another algorithm where we initialize the K-shell of the graph to be the set of all vertices with a degree of at least . We then iteratively remove vertices with a degree less than
from the K-shell until no such vertices remain. The resulting subgraph is the K-Core of the original graph.
Each of these algorithms has its advantages and disadvantages, depending on the properties of the graph we’re analyzing. For example, degree pruning is straightforward but slow on large graphs with many low-degree vertices. Color-coding can sometimes be faster than degree pruning but requires additional memory to store the vertex colors. K-shell decomposition can be faster than both degree pruning and color-coding in some cases but can be more complex to implement and may not work well on graphs with certain degree distributions.
4.1. Example
Now we know about various algorithms for finding the K-Core, let’s look into an example of finding the K-Core of a graph. We’ll use the degree pruning algorithm in this example:
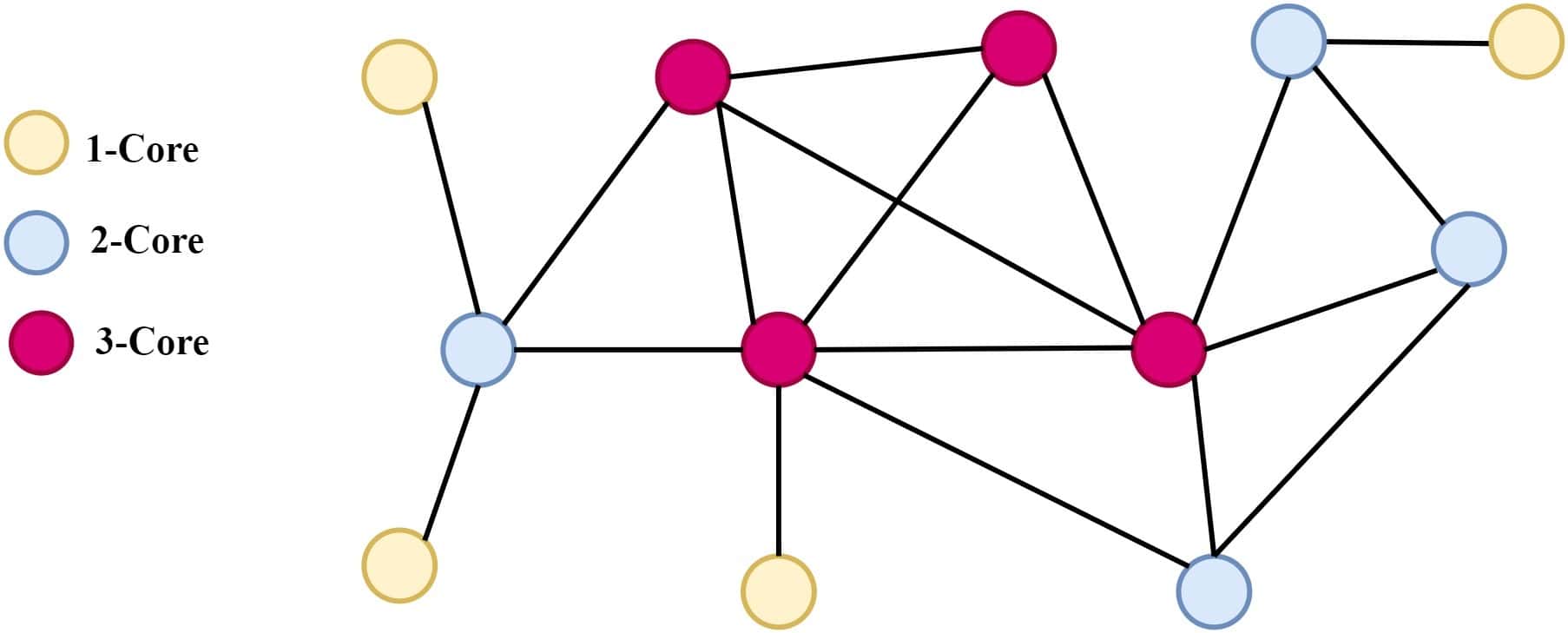
We first find the minimum degree of the graph, which is 1. We then remove all the vertices with degrees less than 1, resulting in the following graph:
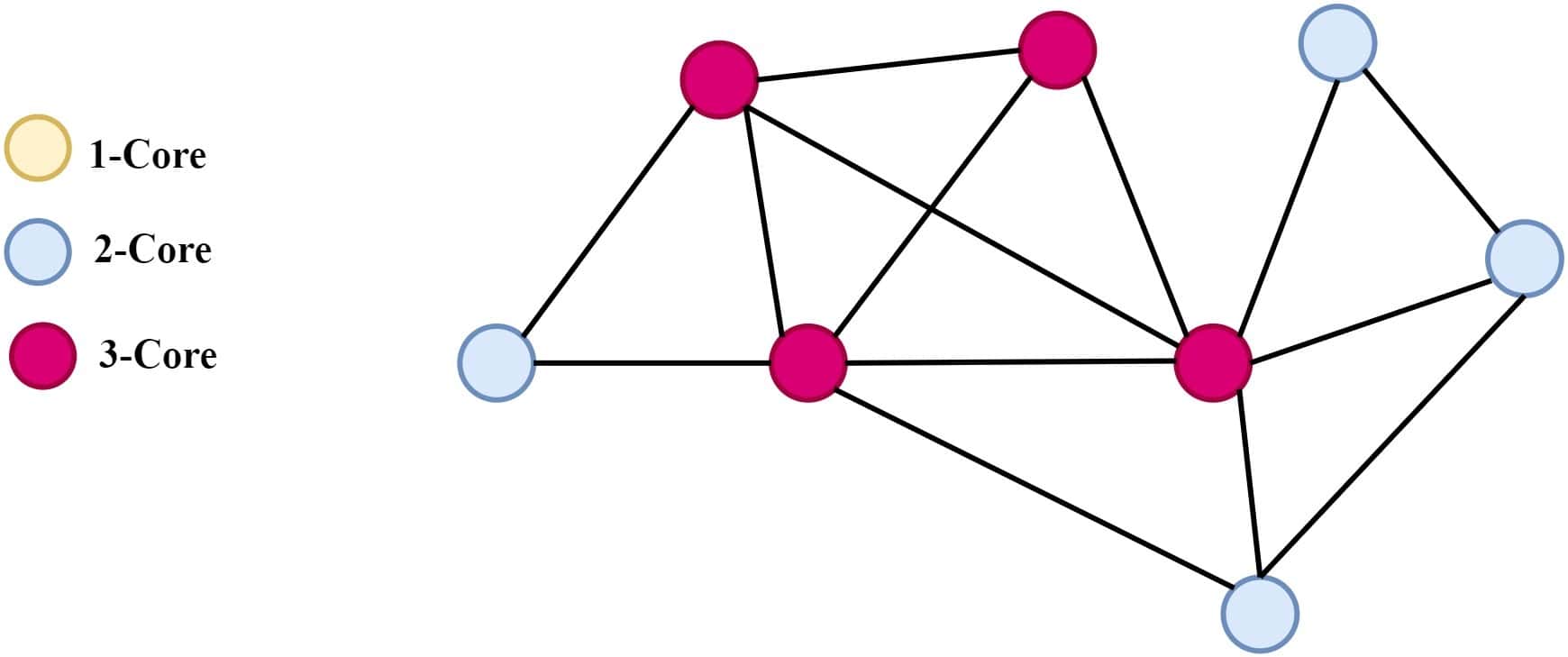
We then find the new minimum degree of the remaining vertices, which is now 2. We then remove all the vertices with degree 2. The resulting graph now looks like this:
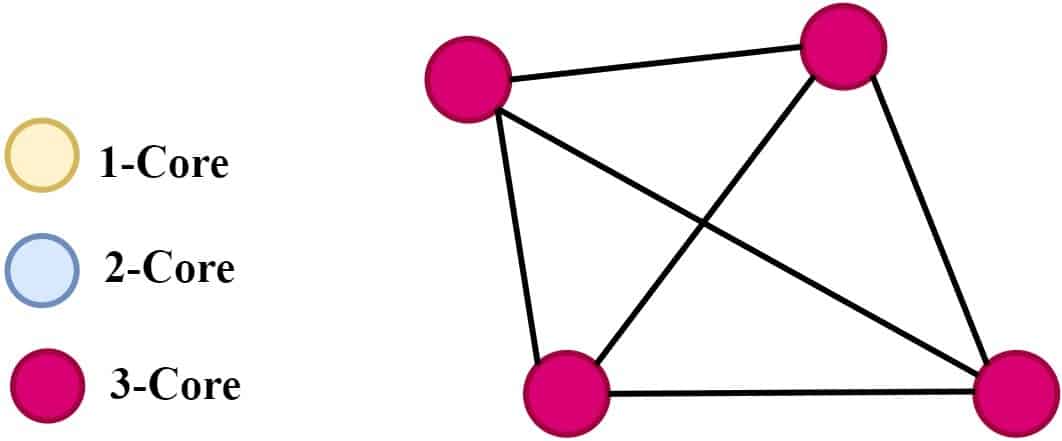
We continue the process until we cannot remove any more nodes, leaving us with the entire graph. The final K-Core for this graph is a 3-core, meaning that every node has a degree of at least 3.
4.2. Algorithm
Let’s take a look at the pseudocode that can be used to calculate the K-Core of a graph:
We first initialized an array of degrees for each vertex and a copy of the original graph. We then iteratively remove vertices with degrees less than and update the degrees of adjacent vertices until no such vertices remain. The resulting subgraph is the K-Core of the original graph.
5. Applications of K-Core
K-core has various applications in different fields, such as social network analysis, recommendation systems, and anomaly detection.
- Social network analysis: We can use K-Core to identify influential users who significantly impact the network’s overall connectivity
- Recommendation systems: We can use the K-Core to recommend products or services to users based on their connectivity to the K-core of the network
- Anomaly detection: we can also use K-Core to identify suspicious transactions in financial networks
- Network robustness: We can use K-Cores to measure the robustness of a network. A network is more robust if it has more K-cores
- Link prediction: We can also use K-Cores to predict which links will likely form in a network
6. Conclusion
In this tutorial, we learned about the K-Core of a graph, its properties, an algorithm to find the K-Core, and its various applications.
Overall, K-Core is a valuable tool for understanding the structure of complex networks. It has several properties and algorithms, that make it an important network science concept. It has applications in various fields, including social network analysis, biology, and computer science.