Geofencing – Determining Whether a Point Is Inside of a Polygon

1. Overview

In this tutorial, we’ll study how to determine whether a point is inside or outside of a polygon.

2. Points and Polygons

2.1. The Problem of Geofencing

The problem of identifying whether a point is inside or outside of a certain polygon is a typical problem of geofencing in geospatial analysis. This problem is common because many real-world applications, such as automated intruder detection and fleet management, require its solution in order to provide the desired services.

Geofencing requires the preliminary identification of a polygon and of a point. Then, we want to determine whether the point is outside of the polygon:

Or, conversely, whether it’s inside of it:

2.2. Geofencing Simple Polygons

For very simple polygons, we might be able to identify some decision rules on the basis of an analytical definition of the polygon:

For the polygon represented in the image above, for example, a point $p$ is inside of its perimeter if the point’s coordinates are $(1 \leq p_x \leq 2, 1 \leq p_y \leq 2)$ .

If we’re able to find a rule-based solution, then we don’t need an algorithm. If the polygon is more complex though, the problem can’t be solved so easily:

In that case, we need a procedure that allows us to determine whether a given point is inside or outside of the shape. This procedure, in turn, should work without requiring the knowledge of the analytical expression of the perimeter, but only the coordinates of the vertices.

3. An Algorithm for Geofencing

In order to justify the application of this algorithm, we first test preliminarily whether the point is in the general area where the polygon lies. We can do this efficiently by comparing the coordinates of the point against those of the smallest rectangle that contains the polygon:

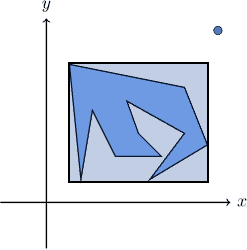
Geofencing Determining Whether a Point is Inside of a Polygon Baeldung

For this test, we simply determine the boundary of the rectangle as $(\text{min}(x), \text{max}(x), \text{min}(y), \text{max}(y))$ . Then, we check whether the point is inside of it. If it isn’t, we consider the point as external to the polygon; otherwise, we proceed further.

3.1. Casting Rays

The even-odd rule algorithm, also called the ray casting algorithm, is then suitable for determining the relative positioning of the polygon and the point. The algorithm is based upon the consideration that, if a point is inside of a polygon, then any ray departing from it meets the perimeter an odd number of times:

If instead, the point is outside the polygon, then any ray meets the perimeter an even number of times:

This consideration is valid regardless of the relative positions of the point and the polygon. But also, it’s valid regardless of the complexity of the polygon or the direction of the ray that’s cast:

3.2. Simplification of the Procedure

In practice, however, the algorithm doesn’t cast an actual and random ray. This is because, in the formulation described above, there are too many degrees of freedom that make a literal implementation of that algorithm computationally inefficient.

Subsequently, to reduce the degrees of freedom of the problem, we prefer to project a horizontal ray from the point. We can do this because the procedure described above is valid for any possible rays. Then, we compute the number of intersections between the horizontal ray, parallel to the $x$ axis, and each of the segments of the polygon:

The polygon, in this context, is the path that corresponds to the ordered, cyclical sequence of 2-tuples representing the coordinates of the vertices. The algorithm iterates over all sequential pairs of vertices and terminates once they’ve all been considered.

Then, for each pair of vertices, it considers whether their $y$ coordinates are simultaneously either above or below the $p_y$ coordinate of the point. If they are, it means that the segment doesn’t intersect the horizontal ray cast from the point:

Next, it compares the $p_x$ coordinate of the point with the $s_x$ coordinate of the point belonging to the current segment, whose $s_y$ coordinate corresponds to $p_y$ . It then checks whether $p_x>s_x$ or, alternatively but consistently, $p_x<s_x$ .

We can calculate $s_x$ with this expression, in relation to the two vertices $u$ and $v$ :

$s_x = u_x + (v_x - u_x) \frac {p_y - u_y} {v_y - u_y}$

Finally, if the conditions of the last two points are both met simultaneously, it then either flips the value of a Boolean variable inside? or it increments a counter numberOfIntersections.

The value of inside? is returned upon reaching termination condition. If we use a counter instead, if the number of intersections found is $2n+1$ , it then declares the point as inside the polygon. Otherwise, the point is outside the polygon.

3.3. Flowchart

This is the flowchart representation of the algorithm:

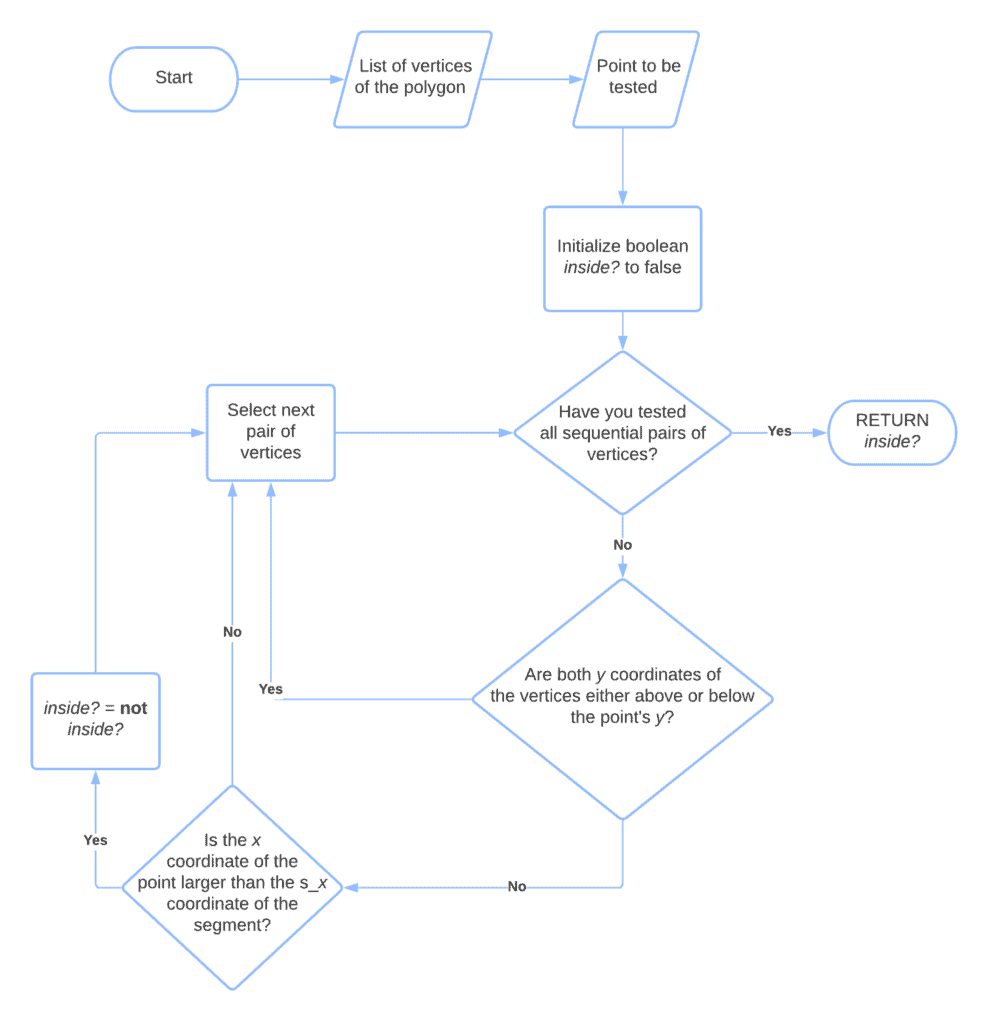
The Boolean variable inside?. that we initialize to false, is the output of the algorithm in this particular implementation.

The main loop of the algorithm iterates over all sequential pairs of vertices in the polygon, defined as tuples containing their coordinates.

We then decide whether the segment that joins the current pair of vertices intersect the horizontal ray cast from the point according to two conditions. If both of them are simultaneously met, then the intersection exists, and in that case, we flip the value of inside?. If either of them isn’t met, we skip to the next pair of vertices in the sequence.

The first condition is that $(u_y > p_y) \neq (v_y > p_y)$ . That is that the two vertices aren’t located on the same semi plane originating from the point’s ray.

If this is true, we also test the second condition. The second condition is that the point’s horizontal position $p_x$ is to the right of the position $s_x$ of the point $s \in \overline{uv}$ . In this particular implementation, we chose to cast a ray to the left of the point $\textbf{p}$ . If we want to cast it to the right of $p$ instead, we simply reverse the expected relative positions of $p$ and $s$ , and test if $p$ is to the left of $s$ .

If this second condition is also met, together with the first, we then flip the value of inside?. The termination condition is the exhaustion of the cyclical path containing the sequential pairs of vertices. Upon reaching it, inside? holds the value True if the point is inside of the polygon, and False otherwise.

4. Practical Applications

We mentioned that the problem of determining the relative position of a polygon and a point has practical applications in geospatial analysis. The two contexts that we cited earlier are the identification of intruders through automatic means and the management of fleets or freights in maritime contexts. Let’s see here why this is the case.

4.1. Protecting Against Physical Threats

Regarding the first case, the legislation traditionally defines trespassing as the crime of unauthorized access to a delimited area that, being either private property or a secure zone, possesses restrictions to entry. Historically, this problem primarily concerns the prevention of burglary against domestic households.

In modern times, though, a major security threat relates to the risk of unmanned terrorist attacks against critical infrastructure. In particular, it relates to the unauthorized access of unmanned aerial vehicles to terminals for international air traffic:

A way to mitigate this risk is to develop and operate a system for the early detection of drones that identifies whether the UAV is inside the perimeter of the infrastructure. This system, in turn, uses an algorithm analogous to the one we described here.

4.2. Managing Autonomous Vessels

Another application concerns the guidance and monitoring of the activity of autonomous vessels. In fact, international maritime law determines that access to areas located near the shoreline of a state is interdicted, unless a vessel receives authorization by the competent maritime authorities.

If we want to develop a system that drives a ship, we thus need to prevent it from inadvertently going into restricted areas. Unfortunately, though, the shoreline in some parts of the world is very complex:

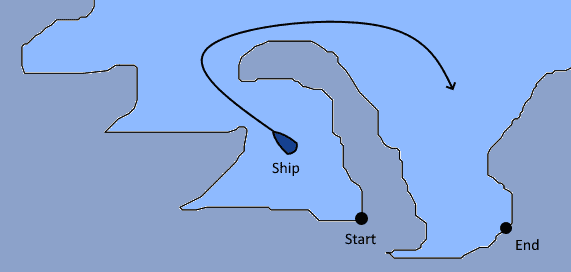
As a consequence, it’s not so easy to determine whether a vessel is inside a restricted portion of the sea.

A solution to this problem consists of the deployment of signaling buoys on the water that can delimit the perimeter of a restricted area. In relation to them, we can then apply our algorithm and determine the relative positions of the ship and the restricted perimeter.

5. Conclusion

In this article, we studied how to determine whether a point is inside a polygon or not.

Full Archive

About Baeldung

Core Concepts

Operating Systems

Artificial Intelligence

Graph Theory

Latex