How to Calculate the Area of a 2D Polygon?

1. Overview

Many ways exist to compute the area of geometric shapes using mathematical formulas. Here, we will focus only on 2D polygons. A polygon consists of a finite number of connected segments that we can represent as a set of consequential points.

There are different formulas to compute the area of regular polygons and several techniques for decomposition. However, the area of non-regular polygons is a bit hard to compute.

In this tutorial, we’ll learn how to calculate the area of an arbitrary 2D polygon using some basic operations from linear algebra.

2. Main Definitions and Operations

First, we must understand a few concepts about 2D vectors and matrices.

2.1. Vector

A vector in a 2D space is a geometric object described by its magnitude and direction or $\upsilon = (a_{1}, a_{2})$ . For example, we can view a vector $\mathbf{\upsilon}$ as the displacement from point $\mathbf{A}$ to point $\mathbf{B}$ :

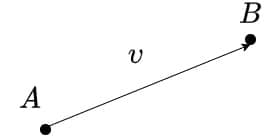
The figure above represents a vector described by two points $A$ and $B$ with coordinates $(x_{1}, y_{1})$ and $(x_{2}, y_{2})$ respectively. Then, the vector is $\upsilon = (x_{2} - x_{1}, y_{2} - y_{1})$ .

2.2. Matrix and Determinant

A matrix is a 2D array of numbers with $m$ rows and $n$ columns. When $m = n$ , the matrix is square and has a determinant, a unique value that characterizes the matrix.

To compute the determinant of a $2 \times 2$ matrix, we should multiply the top-left and bottom-right elements of the matrix (also called the main diagonal). Then, subtract from this the product of the bottom-left and top-right elements:

$\begin{vmatrix}a&b\\c&d\end{vmatrix} = a \times d - b \times c$

3. Area of Triangle

Let’s start by computing the areas of a triangle, and a parallelogram, then extend this to other geometric shapes. Linear algebra provides straightforward formulas to calculate the area of triangles and parallelograms if we know the coordinates of all the vertices on the 2D plane.

So, suppose we have a parallelogram:

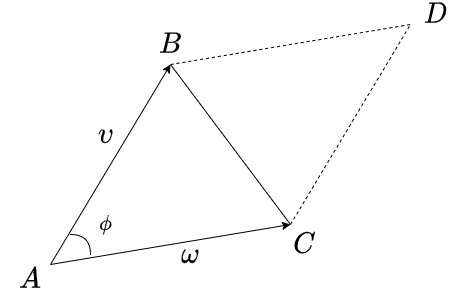
The area of a parallelogram is $S_{ABDC} = |\upsilon||\omega|\sin{\phi}$ . Alternatively, the area is also equivalent to the determinant of a square matrix with vectors $\upsilon$ and $\omega$ as columns: $S_{ABDC} = \begin{vmatrix} \upsilon \times \omega\end{vmatrix}$ .

Consequently, the area of the triangle is: $S_{ABC} = 1 / 2 * \begin{vmatrix} \upsilon \times \omega\end{vmatrix}$ .

For example, let’s compute the area of the following triangle:

$S_{ABC} = 1 / 2 * \begin{vmatrix} \upsilon \times \omega\end{vmatrix} = 1/2 * \begin{vmatrix}(B - A) \times (C - A)\end{vmatrix}$ .

$S_{ABC} = 1 / 2 * \begin{vmatrix}(3 - 0)&(6 - 0)\\(6 - 1)&(2 - 1)\end{vmatrix} = 1/2 * \begin{vmatrix}3&6\\5&1\end{vmatrix} = 1/2 * (3 * 1 - 5 * 6) = -27 / 2$ .

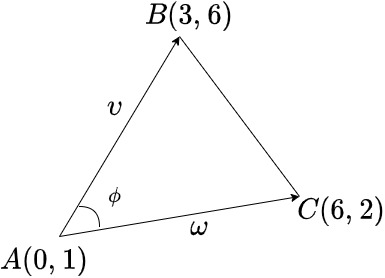
Here, clockwise ordered vectors $\upsilon$ and $\omega$ yield a negative area. Instead, counter-clockwise vectors return a positive area:

$S_{ABC} = 1 / 2 * \begin{vmatrix}(6 - 0)&(3 - 0)\\(2 - 1)&(6 - 1)\end{vmatrix} = 1/2 * \begin{vmatrix}6&3\\1&5\end{vmatrix} = 1/2 * (6 * 5 - 1 * 3) = 27 / 2$ .

This formula for area is a very efficient computation as it doesn’t involve roots or trigonometric functions. Instead, there are just two multiplications, five additions, and possibly one division by two.

4. Area of Polygon

Let’s use this understanding on a generic 2D Polygon.

4.1. Idea of Computation

First, a simple polygon with $\mathbf{n}$ vertices has no self-intersections and can be decomposed into $\mathbf{n}$ triangles. We can calculate the signed areas of each triangle and then add them together to calculate the total area of the polygon. As seen previously, the resulting area can be either positive or negative depending on the order of evaluation.

Mathematically speaking, given $P$ an arbitrary point on the 2D space and $A_{0}, A_{1} ... A_{n - 1}$ the vertices of the polygon and $A_{0} = A_{n - 1}$ to close the polygon. We can compute the area as the sum of all areas of triangles $\triangle P A_{i} A_{i + 1}$ .

4.2. Why It Works

Let’s look at the example of the polygon and point $P$ :

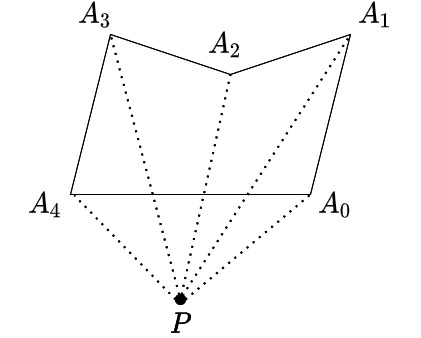
We have to calculate the area of five triangles: $\triangle P A_{0} A_{1}, \triangle P A_{1} A_{2}, \triangle P A_{2} A_{3}, \triangle P A_{3} A_{4}, \triangle P A_{4} A_{0}$ .

Above, we evaluate the orientation of the first four triangles counter-clockwise and the last one clockwise. Therefore, the area of the first four triangles must be positive, and the last one must be negative. This difference will remove the extra area not contained in our polygon. The extra space, in our case, is precisely the triangle: $\triangle P A_{4} A_{0}$ .

4.3. Formula to Compute the Polygon Area

We may choose a specific point $P(0, 0)$ to simplify the final computation formula. Assume we have a polygon represented with the set of $n$ points $A_{0}, A_{1} ... A_{n - 1}$ . Thus, the formula that computes the area of the polygon:

$S_{polygon} = 1 / 2 \times \sum\limits_{i=0}^{n - 1} (x_{i} * y_{i + 1} - y_{i} * x_{i + 1})$ , where $\upsilon_{i} = (x_{i}, y_{i})$ with $i\mod n$ .

Above is the sum of all triangle areas formed with each line segment of a polygon. Remember, we have to include all polygon edges, and the last triangle of the sum will be triangle $\triangle P A_{n - 1} A_{0}$ . Thus, the index $i = i_{actual}\mod n$ .

5. Green’s Formula

Finally, let’s prove the above formula. Referring to mathematical analysis, we should know about Green’s Theorem.

Let $C$ be our polygon line segments. Let $D$ be a region bounded with $C$ . Notice $D$ is our target region. The goal is to compute its area $A$ . Suppose $P(x, y)$ and $Q(x, y)$ are functions, defined on $D$ . Then, Green’s Theorem states:

$\int_C\left(P(x,y)dx+Q(x,y)dy\right) = \int\!\!\!\int_D\left(\frac{\partial}{\partial x}Q(x,y)-\frac{\partial}{\partial y}P(x,y)\right)\,dA$

So, in order to compute the area of polygon $A$ , we need to choose $P(x, y)$ and $Q(x, y)$ such that: $\frac{\partial}{\partial x}Q(x,y)-\frac{\partial}{\partial y}P(x,y) = 1$ . The appropriate choice is $P(x, y) = 0$ and $Q(x, y) = x$ . Thus, if $A$ is our target polygon area, the formula transforms to $A = \int_C xdy$ .

Importantly, $C$ is our polygon line segments $C_{0}, C_{1} ... C_{n - 1}$ and $C = C_{0} \cup C_{1} \cup ... \cup C_{n - 1}$ . And the area: $A = \int_C xdy = \int_{C_{0}} xdy + \int_{C_{1}} xdy+ ... + \int_{C_{n - 1}} xdy$ . Also, we assume all line segments are oriented counter-clockwise.

To compute each integral in the sum, we can represent each line segment: $C_{i} = (x_{i + 1} - x_{i}) * t + x_{i}$ , $(y_{i + 1} - y_{i}) * t + y_{i}$ , $0 \leq t \leq 1$ .

The last thing that we need to do is to substitute the parameterization:

$\int_{C_{i}} xdy = \int_{0}^{1} {((x_{i + 1} - x_{i}) * t + x_{i}) * ( y_{i + 1} - y_{i})}dt$ .

And the final formula that computes the target polygon area:

$A = 1 / 2 \times \sum\limits_{i=0}^{n - 1} {(x_{i + 1} - x_{i}) * ( y_{i + 1} - y_{i})} = 1 / 2 \times \sum\limits_{i=0}^{n - 1} (x_{i} * y_{i + 1} - y_{i} * x_{i + 1})$ .

6. Example of the Polygon Area Calculation

Let’s use the formula just described and calculate the area of the polygon the following polygon

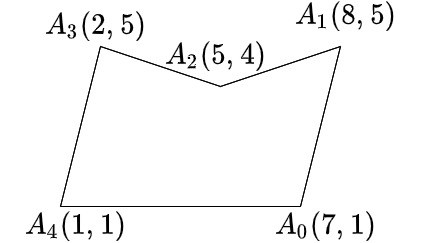
If we choose the point $P (0, 0)$ , then the area is:

$S_{polygon} = 1 / 2 \times\sum\limits_{i=0}^{n - 1} (x_{i} * y_{i + 1} - y_{i} * x_{i + 1})$

$= 1 / 2 \times (\begin{vmatrix} A_{0} \times A_{1}\end{vmatrix} + \begin{vmatrix} A_{1} \times A_{2}\end{vmatrix} + \begin{vmatrix} A_{2} \times A_{3}\end{vmatrix} + \begin{vmatrix} A_{3} \times A_{4}\end{vmatrix} + \begin{vmatrix} A_{4} \times A_{0}\end{vmatrix})$

$= 1 / 2 \times (\begin{vmatrix}7&8\\1&5\end{vmatrix} + \begin{vmatrix}8&5\\5&4\end{vmatrix} + \begin{vmatrix}5&2\\4&5\end{vmatrix} + \begin{vmatrix}2&1\\5&1\end{vmatrix} + \begin{vmatrix}1&7\\1&1\end{vmatrix})$

$= 1 / 2 \times ((7 * 5 - 1 * 8) + (8 * 4 - 5 * 5) + (5 * 5 - 4 * 2) + (2 * 1 - 5 * 1) + (1 * 1 - 7 * 1)) = 1 / 2 \times (35 - 8 + 32 - 25 + 25 - 8 + 2 - 5 + 1 - 7) = 42 / 2 = 21$

To emphasize, notice that our target point $P (0, 0)$ is on the bottom-left of our polygon. As a consequence the areas of $\triangle P A_{0} A_{1}, \triangle P A_{1} A_{2}, \triangle P A_{2} A_{3}$ are positive and the areas of $\triangle P A_{3} A_{4}, \triangle P A_{4} A_{0}$ are negative. As expected, the extra computed area is exactly $\triangle P A_{3} A_{4}$ and $\triangle P A_{4} A_{0}$ .

7. Conclusion

In this article, we’ve introduced a way to calculate the area of a 2D polygon. Furthermore, we’ve touched on some major topics of linear algebra. Moreover, we also introduced methods to calculate the area of the triangle and parallelogram, as they are specific polygons.

Full Archive

About Baeldung